Causal Head Gating: A Framework for Interpreting Roles of Attention Heads in Transformers

We present causal head gating (CHG), a scalable method for interpreting the functional roles of attention heads in transformer models. CHG learns soft gates over heads and assigns them a causal taxonomy - facilitating, interfering, or irrelevant - based on their impact on task performance. Unlike prior approaches in mechanistic interpretability, which are hypothesis-driven and require prompt templates or target labels, CHG applies directly to any dataset using standard next-token prediction. We evaluate CHG across multiple large language models (LLMs) in the Llama 3 model family and diverse tasks, including syntax, commonsense, and mathematical reasoning, and show that CHG scores yield causal - not merely correlational - insight, validated via ablation and causal mediation analyses. We also introduce contrastive CHG, a variant that isolates sub-circuits for specific task components. Our findings reveal that LLMs contain multiple sparse, sufficient sub-circuits, that individual head roles depend on interactions with others (low modularity), and that instruction following and in-context learning rely on separable mechanisms.

Understanding Task Representations in Neural Networks via Bayesian Ablation

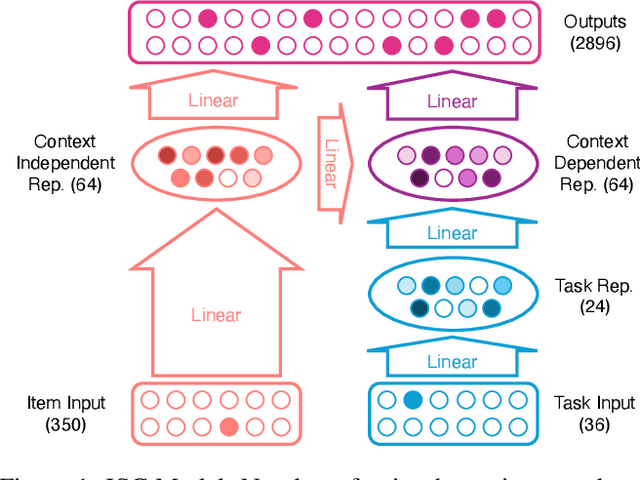
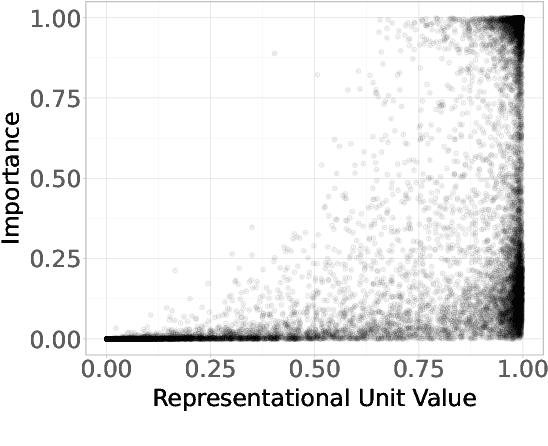
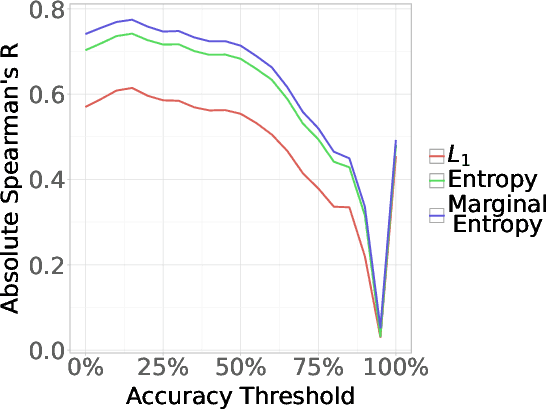
Neural networks are powerful tools for cognitive modeling due to their flexibility and emergent properties. However, interpreting their learned representations remains challenging due to their sub-symbolic semantics. In this work, we introduce a novel probabilistic framework for interpreting latent task representations in neural networks. Inspired by Bayesian inference, our approach defines a distribution over representational units to infer their causal contributions to task performance. Using ideas from information theory, we propose a suite of tools and metrics to illuminate key model properties, including representational distributedness, manifold complexity, and polysemanticity.

Connecting Context-specific Adaptation in Humans to Meta-learning

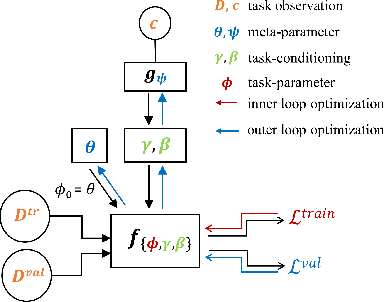
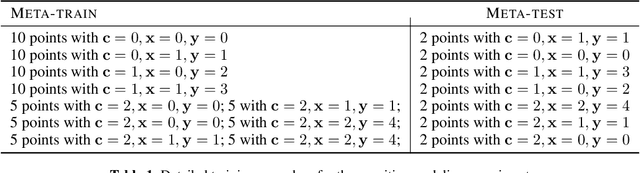
Cognitive control, the ability of a system to adapt to the demands of a task, is an integral part of cognition. A widely accepted fact about cognitive control is that it is context-sensitive: Adults and children alike infer information about a task's demands from contextual cues and use these inferences to learn from ambiguous cues. However, the precise way in which people use contextual cues to guide adaptation to a new task remains poorly understood. This work connects the context-sensitive nature of cognitive control to a method for meta-learning with context-conditioned adaptation. We begin by identifying an essential difference between human learning and current approaches to meta-learning: In contrast to humans, existing meta-learning algorithms do not make use of task-specific contextual cues but instead rely exclusively on online feedback in the form of task-specific labels or rewards. To remedy this, we introduce a framework for using contextual information about a task to guide the initialization of task-specific models before adaptation to online feedback. We show how context-conditioned meta-learning can capture human behavior in a cognitive task and how it can be scaled to improve the speed of learning in various settings, including few-shot classification and low-sample reinforcement learning. Our work demonstrates that guiding meta-learning with task information can capture complex, human-like behavior, thereby deepening our understanding of cognitive control.

Recasting Gradient-Based Meta-Learning as Hierarchical Bayes

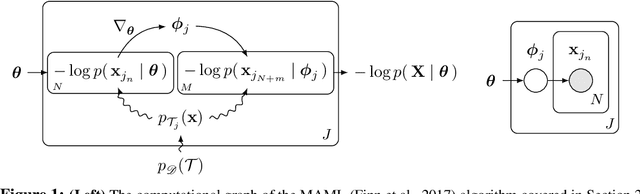
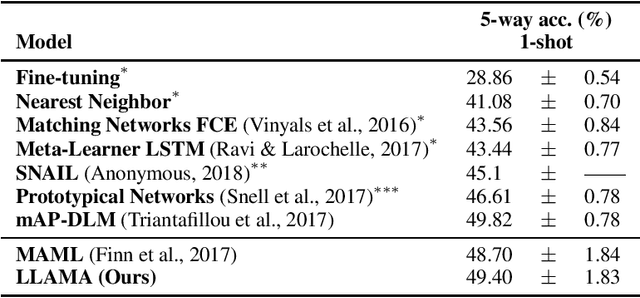
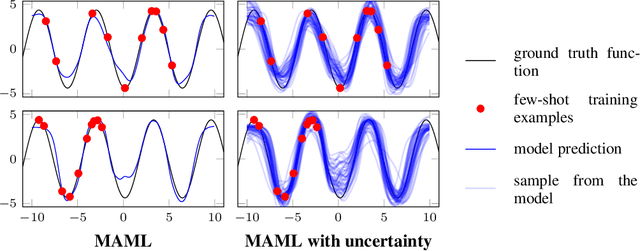
Meta-learning allows an intelligent agent to leverage prior learning episodes as a basis for quickly improving performance on a novel task. Bayesian hierarchical modeling provides a theoretical framework for formalizing meta-learning as inference for a set of parameters that are shared across tasks. Here, we reformulate the model-agnostic meta-learning algorithm (MAML) of Finn et al. (2017) as a method for probabilistic inference in a hierarchical Bayesian model. In contrast to prior methods for meta-learning via hierarchical Bayes, MAML is naturally applicable to complex function approximators through its use of a scalable gradient descent procedure for posterior inference. Furthermore, the identification of MAML as hierarchical Bayes provides a way to understand the algorithm's operation as a meta-learning procedure, as well as an opportunity to make use of computational strategies for efficient inference. We use this opportunity to propose an improvement to the MAML algorithm that makes use of techniques from approximate inference and curvature estimation.

Evaluating computational models of explanation using human judgments

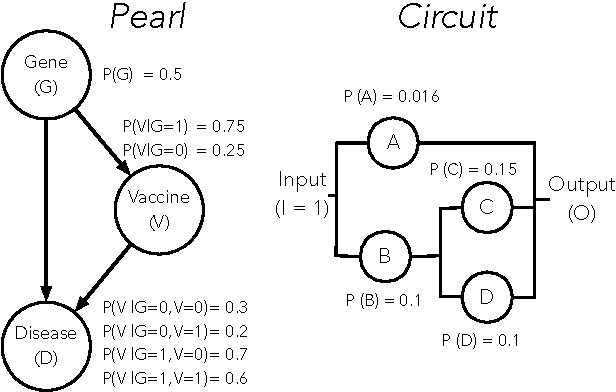
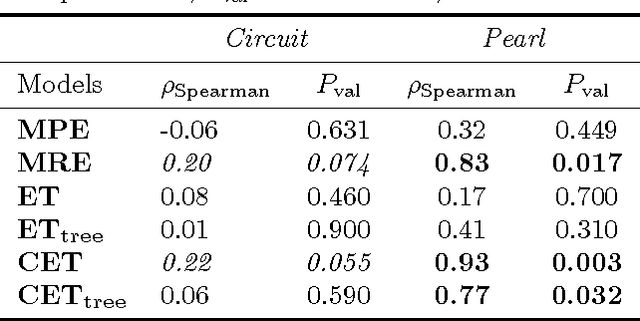
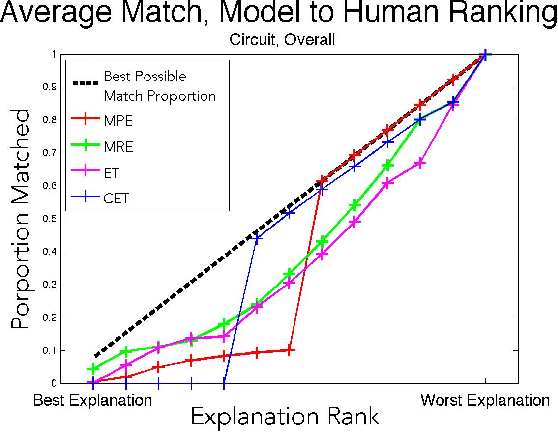
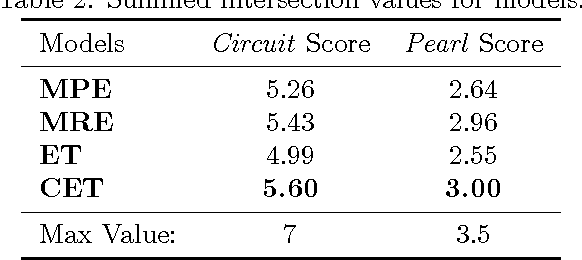
We evaluate four computational models of explanation in Bayesian networks by comparing model predictions to human judgments. In two experiments, we present human participants with causal structures for which the models make divergent predictions and either solicit the best explanation for an observed event (Experiment 1) or have participants rate provided explanations for an observed event (Experiment 2). Across two versions of two causal structures and across both experiments, we find that the Causal Explanation Tree and Most Relevant Explanation models provide better fits to human data than either Most Probable Explanation or Explanation Tree models. We identify strengths and shortcomings of these models and what they can reveal about human explanation. We conclude by suggesting the value of pursuing computational and psychological investigations of explanation in parallel.

The Author-Topic Model for Authors and Documents

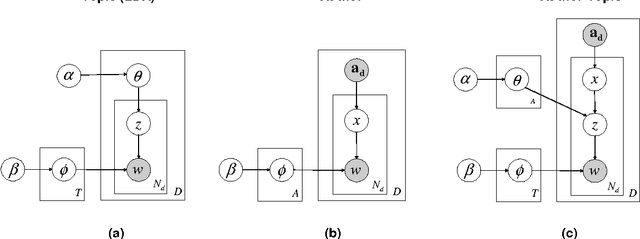
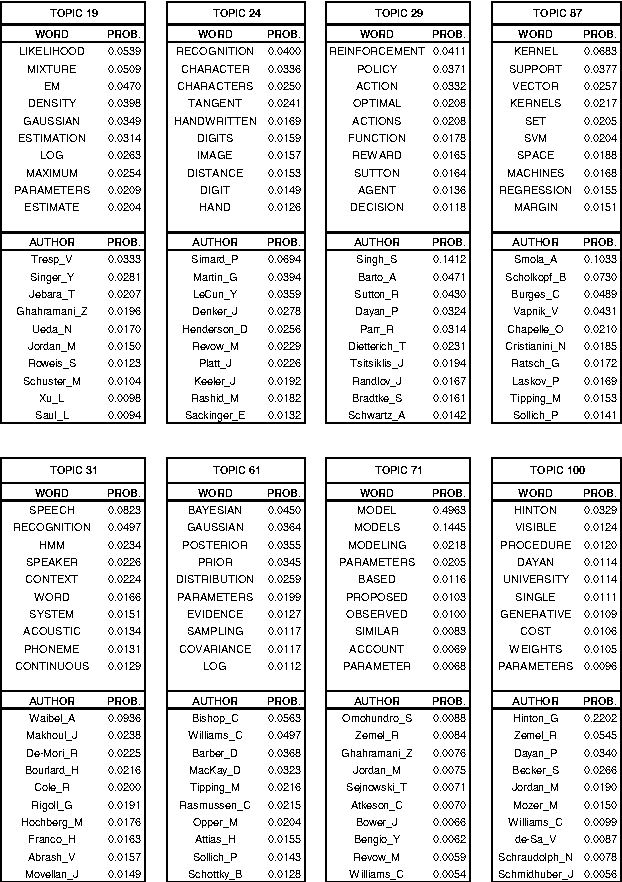
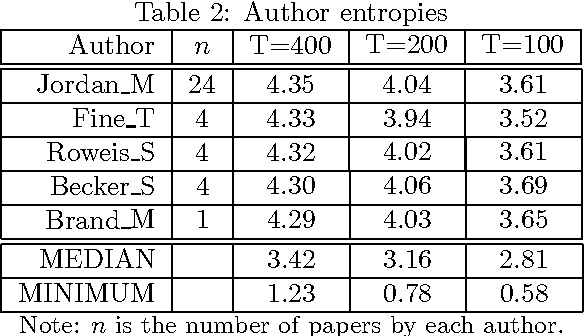
We introduce the author-topic model, a generative model for documents that extends Latent Dirichlet Allocation (LDA; Blei, Ng, & Jordan, 2003) to include authorship information. Each author is associated with a multinomial distribution over topics and each topic is associated with a multinomial distribution over words. A document with multiple authors is modeled as a distribution over topics that is a mixture of the distributions associated with the authors. We apply the model to a collection of 1,700 NIPS conference papers and 160,000 CiteSeer abstracts. Exact inference is intractable for these datasets and we use Gibbs sampling to estimate the topic and author distributions. We compare the performance with two other generative models for documents, which are special cases of the author-topic model: LDA (a topic model) and a simple author model in which each author is associated with a distribution over words rather than a distribution over topics. We show topics recovered by the author-topic model, and demonstrate applications to computing similarity between authors and entropy of author output.

A Non-Parametric Bayesian Method for Inferring Hidden Causes

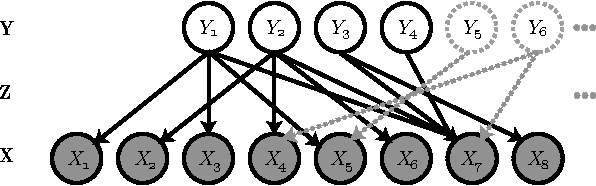
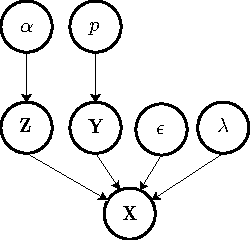
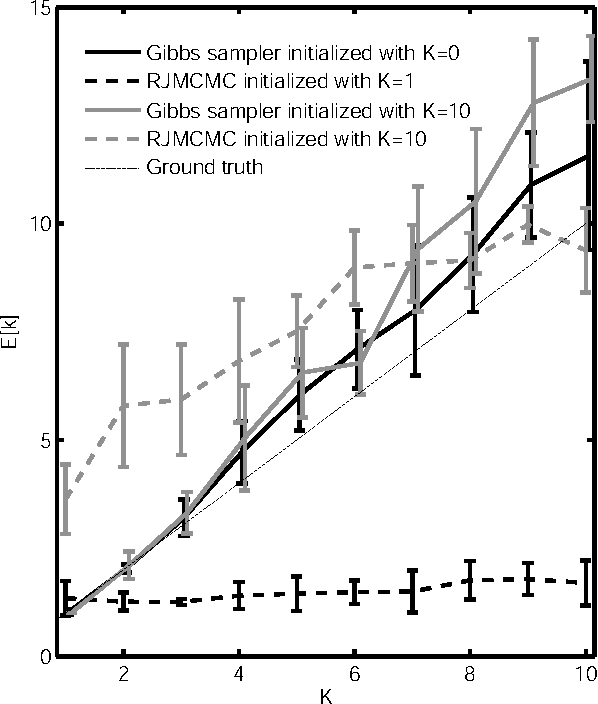
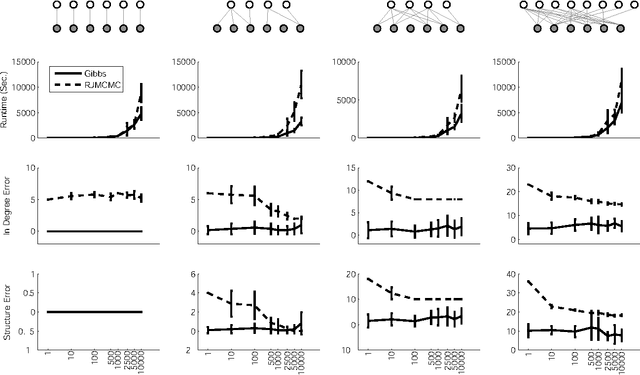
We present a non-parametric Bayesian approach to structure learning with hidden causes. Previous Bayesian treatments of this problem define a prior over the number of hidden causes and use algorithms such as reversible jump Markov chain Monte Carlo to move between solutions. In contrast, we assume that the number of hidden causes is unbounded, but only a finite number influence observable variables. This makes it possible to use a Gibbs sampler to approximate the distribution over causal structures. We evaluate the performance of both approaches in discovering hidden causes in simulated data, and use our non-parametric approach to discover hidden causes in a real medical dataset.

Structured Priors for Structure Learning

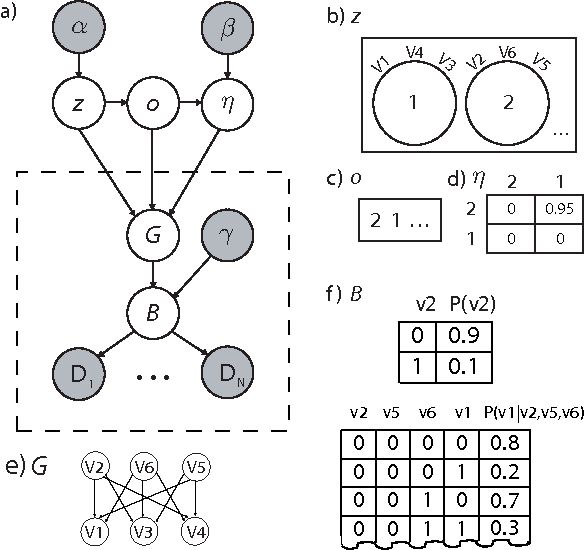
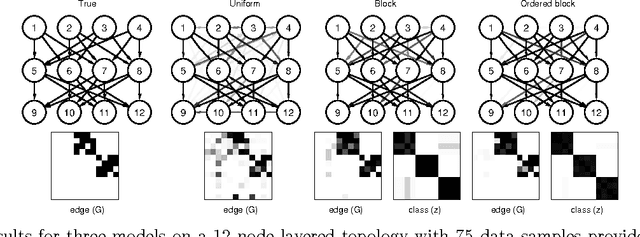
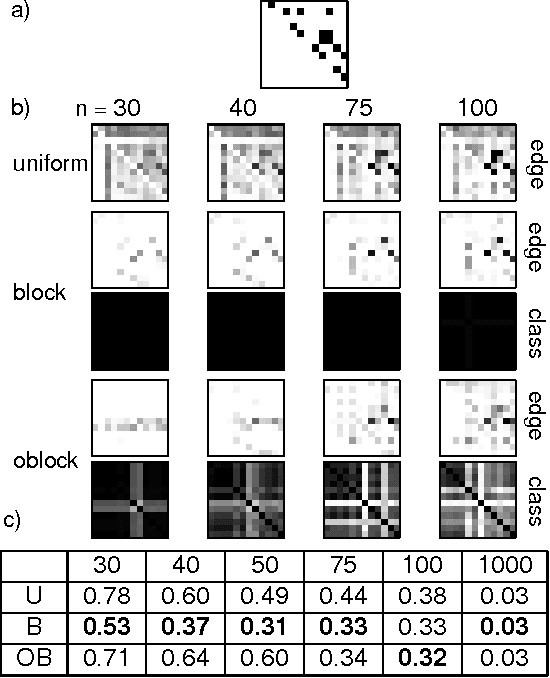
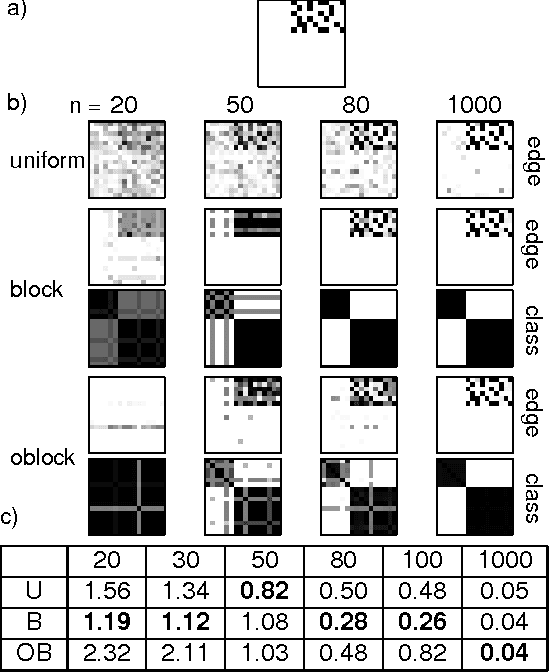
Traditional approaches to Bayes net structure learning typically assume little regularity in graph structure other than sparseness. However, in many cases, we expect more systematicity: variables in real-world systems often group into classes that predict the kinds of probabilistic dependencies they participate in. Here we capture this form of prior knowledge in a hierarchical Bayesian framework, and exploit it to enable structure learning and type discovery from small datasets. Specifically, we present a nonparametric generative model for directed acyclic graphs as a prior for Bayes net structure learning. Our model assumes that variables come in one or more classes and that the prior probability of an edge existing between two variables is a function only of their classes. We derive an MCMC algorithm for simultaneous inference of the number of classes, the class assignments of variables, and the Bayes net structure over variables. For several realistic, sparse datasets, we show that the bias towards systematicity of connections provided by our model yields more accurate learned networks than a traditional, uniform prior approach, and that the classes found by our model are appropriate.

The Phylogenetic Indian Buffet Process: A Non-Exchangeable Nonparametric Prior for Latent Features

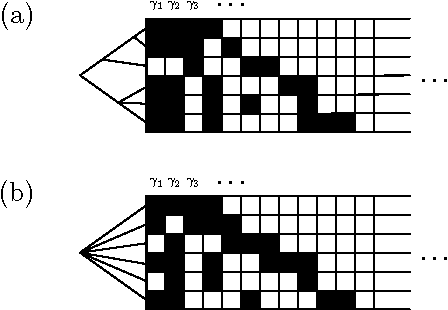
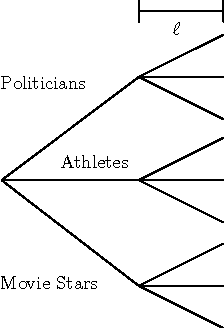
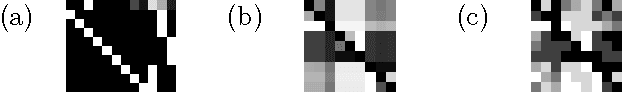
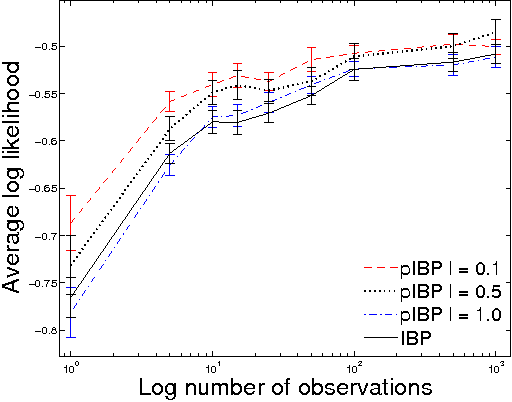
Nonparametric Bayesian models are often based on the assumption that the objects being modeled are exchangeable. While appropriate in some applications (e.g., bag-of-words models for documents), exchangeability is sometimes assumed simply for computational reasons; non-exchangeable models might be a better choice for applications based on subject matter. Drawing on ideas from graphical models and phylogenetics, we describe a non-exchangeable prior for a class of nonparametric latent feature models that is nearly as efficient computationally as its exchangeable counterpart. Our model is applicable to the general setting in which the dependencies between objects can be expressed using a tree, where edge lengths indicate the strength of relationships. We demonstrate an application to modeling probabilistic choice.