Tight Second-Order Certificates for Randomized Smoothing

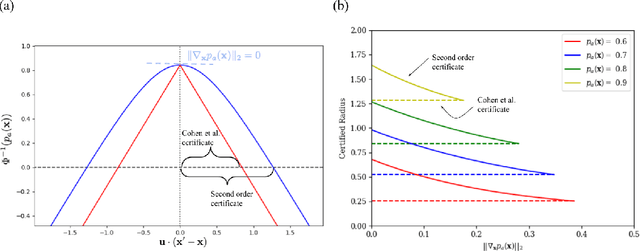
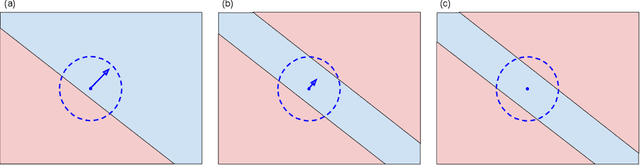
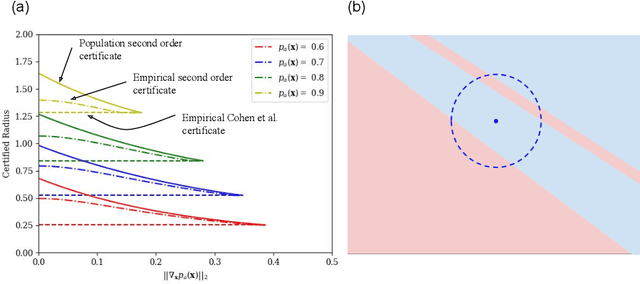
Randomized smoothing is a popular way of providing robustness guarantees against adversarial attacks: randomly-smoothed functions have a universal Lipschitz-like bound, allowing for robustness certificates to be easily computed. In this work, we show that there also exists a universal curvature-like bound for Gaussian random smoothing: given the exact value and gradient of a smoothed function, we compute a lower bound on the distance of a point to its closest adversarial example, called the Second-order Smoothing (SoS) robustness certificate. In addition to proving the correctness of this novel certificate, we show that SoS certificates are realizable and therefore tight. Interestingly, we show that the maximum achievable benefits, in terms of certified robustness, from using the additional information of the gradient norm are relatively small: because our bounds are tight, this is a fundamental negative result. The gain of SoS certificates further diminishes if we consider the estimation error of the gradient norms, for which we have developed an estimator. We therefore additionally develop a variant of Gaussian smoothing, called \textit{Gaussian dipole smoothing}, which provides similar bounds to randomized smoothing with gradient information, but with much-improved sample efficiency. This allows us to achieve (marginally) improved robustness certificates on high-dimensional datasets such as CIFAR-10 and ImageNet. Code is available at https://github.com/alevine0/smoothing_second_order.

Network Deconvolution

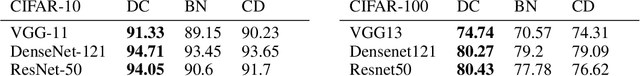
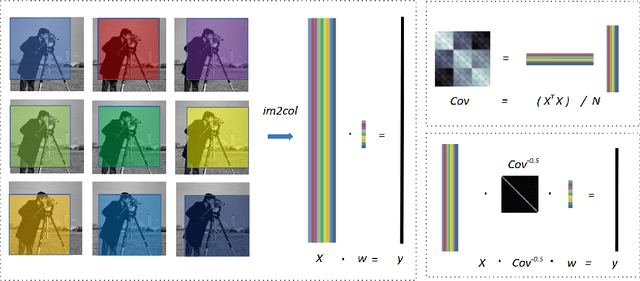
Convolution is a central operation in Convolutional Neural Networks (CNNs), which applies a kernel or mask to overlapping regions shifted across the image. In this work we show that the underlying kernels are trained with highly correlated data, which leads to co-adaptation of model weights. To address this issue we propose what we call network deconvolution, a procedure that aims to remove pixel-wise and channel-wise correlations before the data is fed into each layer. We show that by removing this correlation we are able to achieve better convergence rates during model training with superior results without the use of batch normalization on the CIFAR-10, CIFAR-100, MNIST, Fashion-MNIST datasets, as well as against reference models from "model zoo" on the ImageNet standard benchmark.

ShapeFit and ShapeKick for Robust, Scalable Structure from Motion

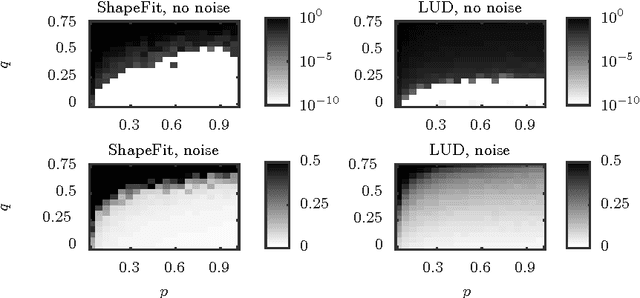
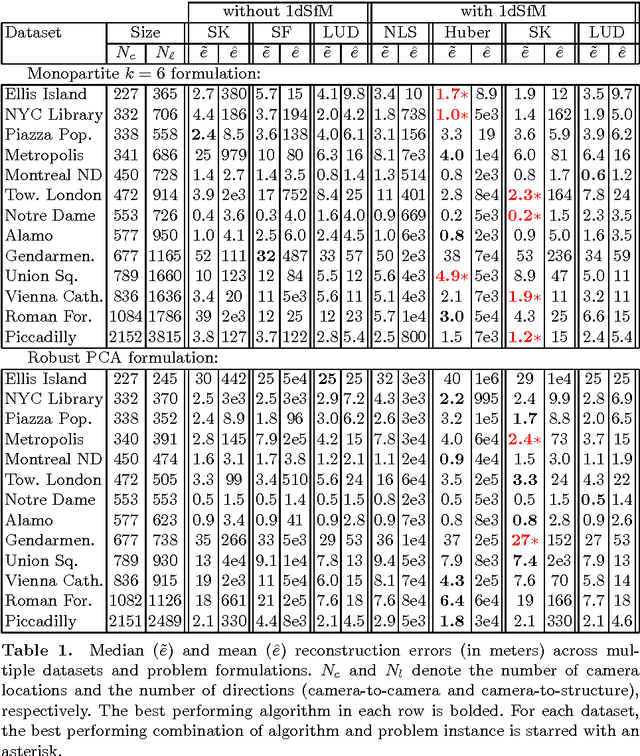
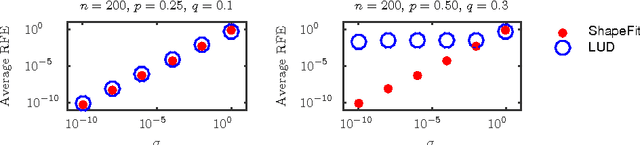
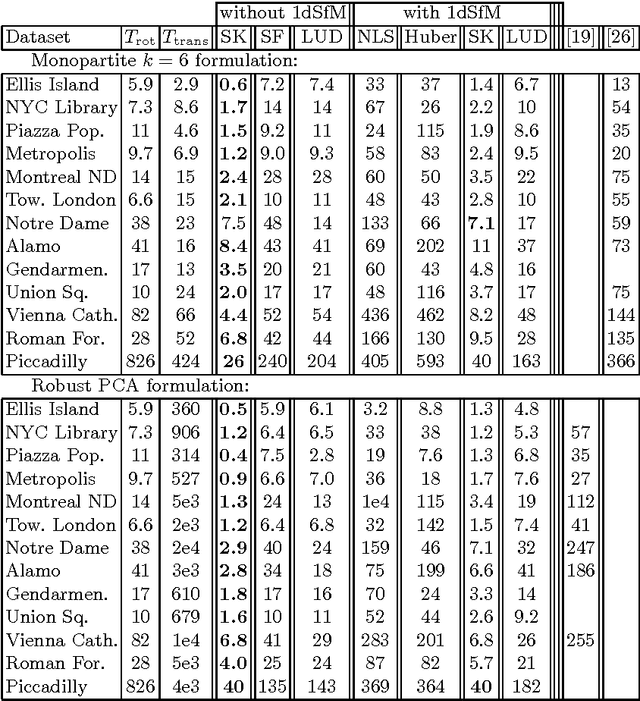
We introduce a new method for location recovery from pair-wise directions that leverages an efficient convex program that comes with exact recovery guarantees, even in the presence of adversarial outliers. When pairwise directions represent scaled relative positions between pairs of views (estimated for instance with epipolar geometry) our method can be used for location recovery, that is the determination of relative pose up to a single unknown scale. For this task, our method yields performance comparable to the state-of-the-art with an order of magnitude speed-up. Our proposed numerical framework is flexible in that it accommodates other approaches to location recovery and can be used to speed up other methods. These properties are demonstrated by extensively testing against state-of-the-art methods for location recovery on 13 large, irregular collections of images of real scenes in addition to simulated data with ground truth.

Layer-Specific Adaptive Learning Rates for Deep Networks

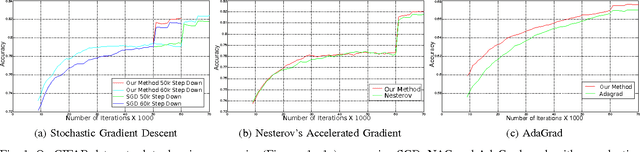
The increasing complexity of deep learning architectures is resulting in training time requiring weeks or even months. This slow training is due in part to vanishing gradients, in which the gradients used by back-propagation are extremely large for weights connecting deep layers (layers near the output layer), and extremely small for shallow layers (near the input layer); this results in slow learning in the shallow layers. Additionally, it has also been shown that in highly non-convex problems, such as deep neural networks, there is a proliferation of high-error low curvature saddle points, which slows down learning dramatically. In this paper, we attempt to overcome the two above problems by proposing an optimization method for training deep neural networks which uses learning rates which are both specific to each layer in the network and adaptive to the curvature of the function, increasing the learning rate at low curvature points. This enables us to speed up learning in the shallow layers of the network and quickly escape high-error low curvature saddle points. We test our method on standard image classification datasets such as MNIST, CIFAR10 and ImageNet, and demonstrate that our method increases accuracy as well as reduces the required training time over standard algorithms.

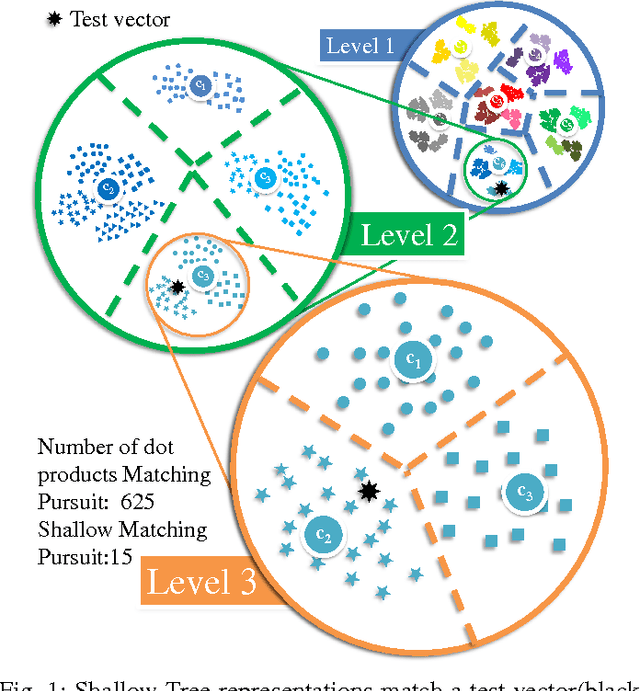
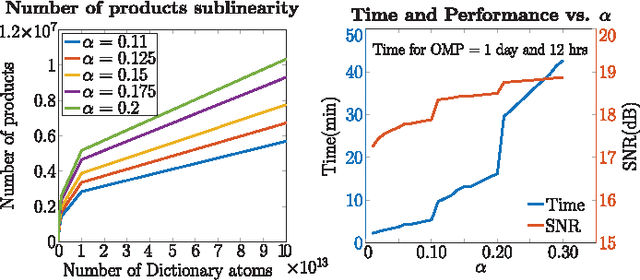
Fast Sublinear Sparse Representation using Shallow Tree Matching Pursuit

Sparse approximations using highly over-complete dictionaries is a state-of-the-art tool for many imaging applications including denoising, super-resolution, compressive sensing, light-field analysis, and object recognition. Unfortunately, the applicability of such methods is severely hampered by the computational burden of sparse approximation: these algorithms are linear or super-linear in both the data dimensionality and size of the dictionary. We propose a framework for learning the hierarchical structure of over-complete dictionaries that enables fast computation of sparse representations. Our method builds on tree-based strategies for nearest neighbor matching, and presents domain-specific enhancements that are highly efficient for the analysis of image patches. Contrary to most popular methods for building spatial data structures, out methods rely on shallow, balanced trees with relatively few layers. We show an extensive array of experiments on several applications such as image denoising/superresolution, compressive video/light-field sensing where we practically achieve 100-1000x speedup (with a less than 1dB loss in accuracy).