Choongbum Lee
ShapeFit and ShapeKick for Robust, Scalable Structure from Motion
Aug 07, 2016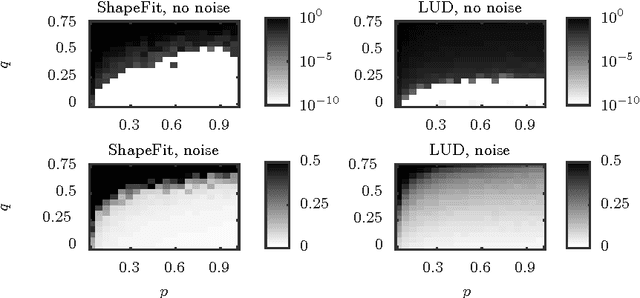
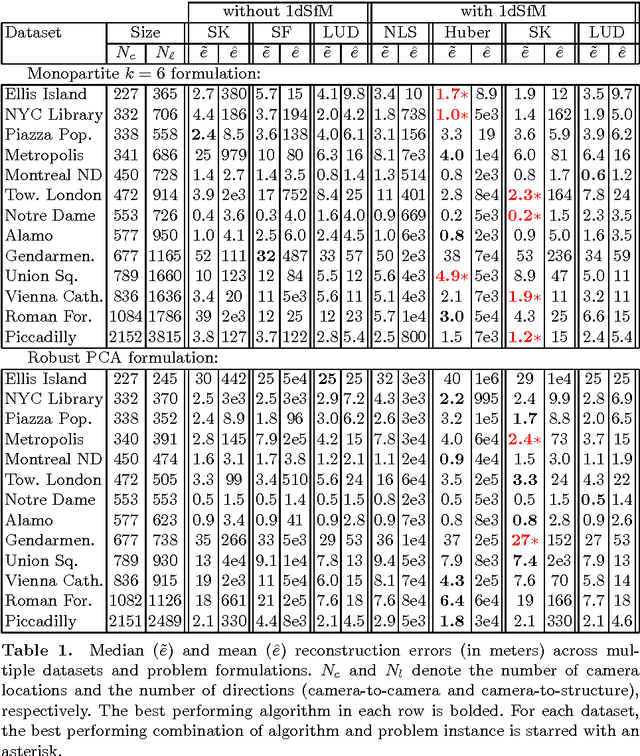
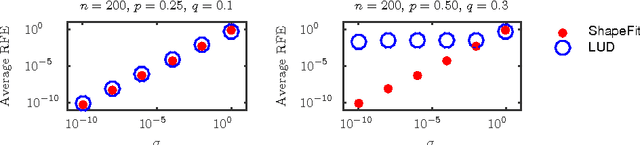
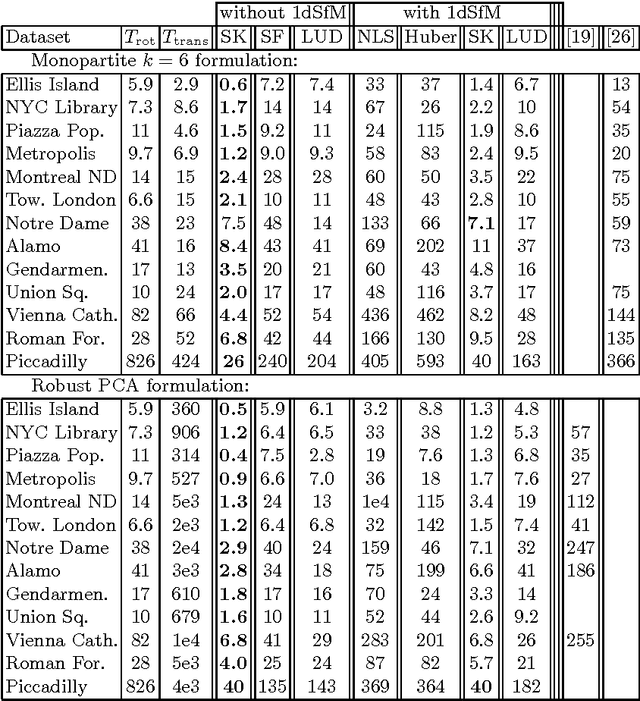
Abstract:We introduce a new method for location recovery from pair-wise directions that leverages an efficient convex program that comes with exact recovery guarantees, even in the presence of adversarial outliers. When pairwise directions represent scaled relative positions between pairs of views (estimated for instance with epipolar geometry) our method can be used for location recovery, that is the determination of relative pose up to a single unknown scale. For this task, our method yields performance comparable to the state-of-the-art with an order of magnitude speed-up. Our proposed numerical framework is flexible in that it accommodates other approaches to location recovery and can be used to speed up other methods. These properties are demonstrated by extensively testing against state-of-the-art methods for location recovery on 13 large, irregular collections of images of real scenes in addition to simulated data with ground truth.
Exact simultaneous recovery of locations and structure from known orientations and corrupted point correspondences
Sep 16, 2015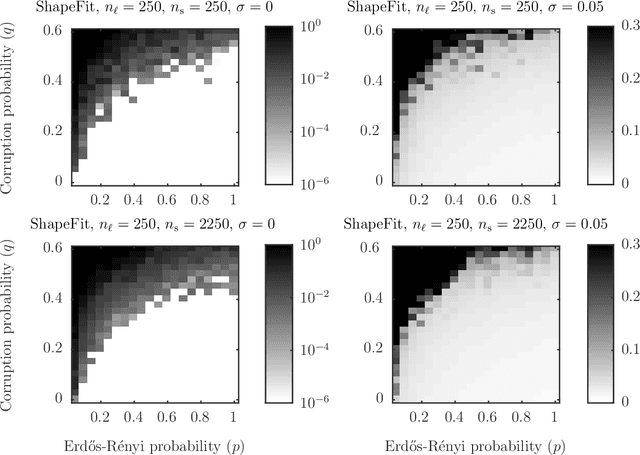
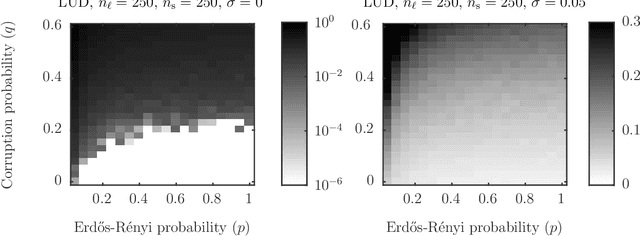
Abstract:Let $t_1,\ldots,t_{n_l} \in \mathbb{R}^d$ and $p_1,\ldots,p_{n_s} \in \mathbb{R}^d$ and consider the bipartite location recovery problem: given a subset of pairwise direction observations $\{(t_i - p_j) / \|t_i - p_j\|_2\}_{i,j \in [n_l] \times [n_s]}$, where a constant fraction of these observations are arbitrarily corrupted, find $\{t_i\}_{i \in [n_ll]}$ and $\{p_j\}_{j \in [n_s]}$ up to a global translation and scale. We study the recently introduced ShapeFit algorithm as a method for solving this bipartite location recovery problem. In this case, ShapeFit consists of a simple convex program over $d(n_l + n_s)$ real variables. We prove that this program recovers a set of $n_l+n_s$ i.i.d. Gaussian locations exactly and with high probability if the observations are given by a bipartite Erd\H{o}s-R\'{e}nyi graph, $d$ is large enough, and provided that at most a constant fraction of observations involving any particular location are adversarially corrupted. This recovery theorem is based on a set of deterministic conditions that we prove are sufficient for exact recovery. Finally, we propose a modified pipeline for the Structure for Motion problem, based on this bipartite location recovery problem.
ShapeFit: Exact location recovery from corrupted pairwise directions
Jul 04, 2015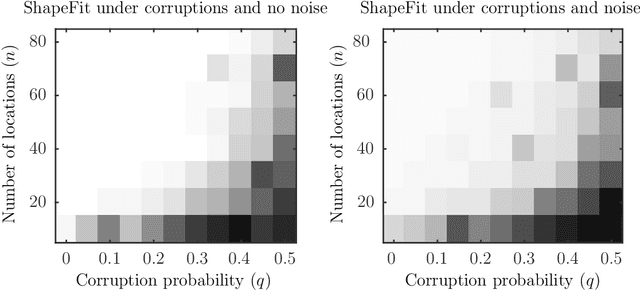
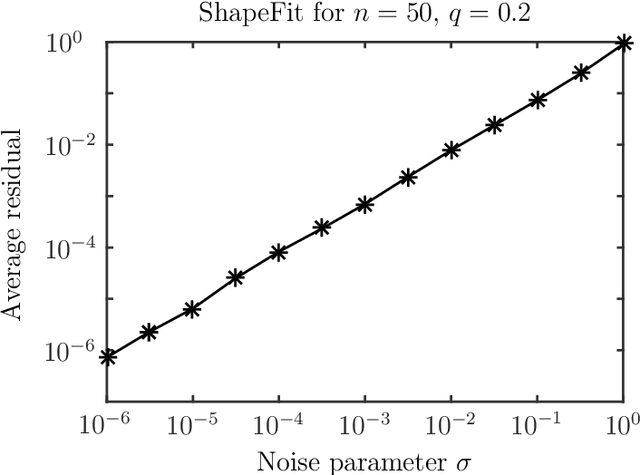
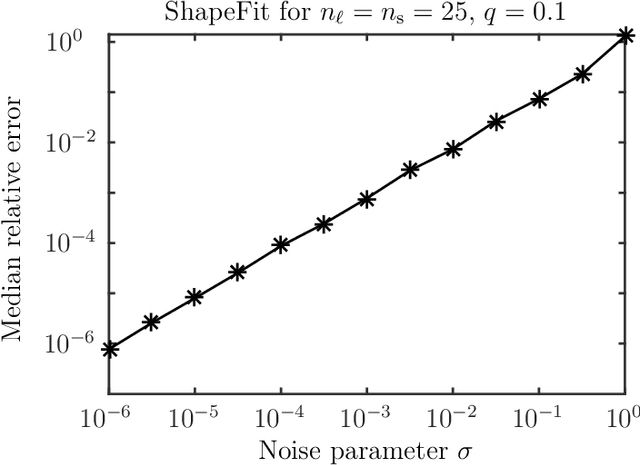
Abstract:Let $t_1,\ldots,t_n \in \mathbb{R}^d$ and consider the location recovery problem: given a subset of pairwise direction observations $\{(t_i - t_j) / \|t_i - t_j\|_2\}_{i<j \in [n] \times [n]}$, where a constant fraction of these observations are arbitrarily corrupted, find $\{t_i\}_{i=1}^n$ up to a global translation and scale. We propose a novel algorithm for the location recovery problem, which consists of a simple convex program over $dn$ real variables. We prove that this program recovers a set of $n$ i.i.d. Gaussian locations exactly and with high probability if the observations are given by an \erdosrenyi graph, $d$ is large enough, and provided that at most a constant fraction of observations involving any particular location are adversarially corrupted. We also prove that the program exactly recovers Gaussian locations for $d=3$ if the fraction of corrupted observations at each location is, up to poly-logarithmic factors, at most a constant. Both of these recovery theorems are based on a set of deterministic conditions that we prove are sufficient for exact recovery.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge