Exact simultaneous recovery of locations and structure from known orientations and corrupted point correspondences
Paper and Code
Sep 16, 2015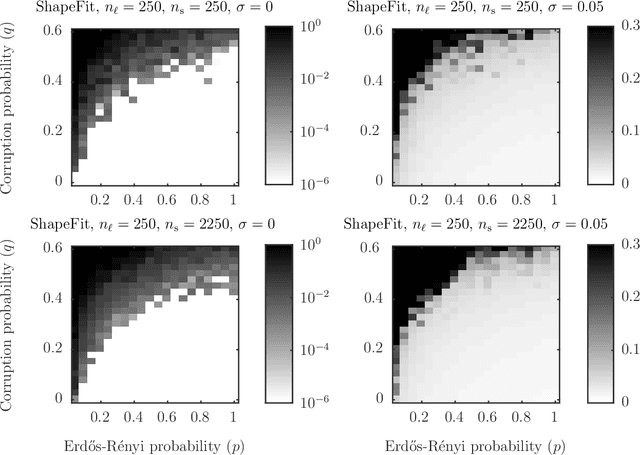
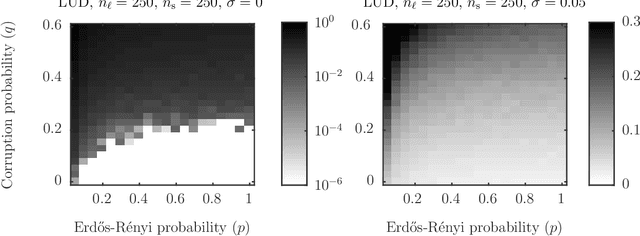
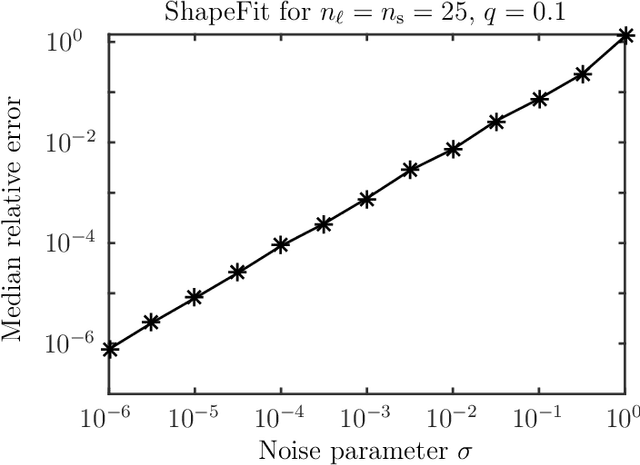
Let $t_1,\ldots,t_{n_l} \in \mathbb{R}^d$ and $p_1,\ldots,p_{n_s} \in \mathbb{R}^d$ and consider the bipartite location recovery problem: given a subset of pairwise direction observations $\{(t_i - p_j) / \|t_i - p_j\|_2\}_{i,j \in [n_l] \times [n_s]}$, where a constant fraction of these observations are arbitrarily corrupted, find $\{t_i\}_{i \in [n_ll]}$ and $\{p_j\}_{j \in [n_s]}$ up to a global translation and scale. We study the recently introduced ShapeFit algorithm as a method for solving this bipartite location recovery problem. In this case, ShapeFit consists of a simple convex program over $d(n_l + n_s)$ real variables. We prove that this program recovers a set of $n_l+n_s$ i.i.d. Gaussian locations exactly and with high probability if the observations are given by a bipartite Erd\H{o}s-R\'{e}nyi graph, $d$ is large enough, and provided that at most a constant fraction of observations involving any particular location are adversarially corrupted. This recovery theorem is based on a set of deterministic conditions that we prove are sufficient for exact recovery. Finally, we propose a modified pipeline for the Structure for Motion problem, based on this bipartite location recovery problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge