Vladislav Voroninski
Optimal Sample Complexity of Gradient Descent for Amplitude Flow via Non-Lipschitz Matrix Concentration
Oct 31, 2020Abstract:We consider the problem of recovering a real-valued $n$-dimensional signal from $m$ phaseless, linear measurements and analyze the amplitude-based non-smooth least squares objective. We establish local convergence of gradient descent with optimal sample complexity based on the uniform concentration of a random, discontinuous matrix-valued operator arising from the objective's gradient dynamics. While common techniques to establish uniform concentration of random functions exploit Lipschitz continuity, we prove that the discontinuous matrix-valued operator satisfies a uniform matrix concentration inequality when the measurement vectors are Gaussian as soon as $m = \Omega(n)$ with high probability. We then show that satisfaction of this inequality is sufficient for gradient descent with proper initialization to converge linearly to the true solution up to the global sign ambiguity. As a consequence, this guarantees local convergence for Gaussian measurements at optimal sample complexity. The concentration methods in the present work have previously been used to establish recovery guarantees for a variety of inverse problems under generative neural network priors. This paper demonstrates the applicability of these techniques to more traditional inverse problems and serves as a pedagogical introduction to those results.
Compressive Phase Retrieval: Optimal Sample Complexity with Deep Generative Priors
Aug 24, 2020


Abstract:Advances in compressive sensing provided reconstruction algorithms of sparse signals from linear measurements with optimal sample complexity, but natural extensions of this methodology to nonlinear inverse problems have been met with potentially fundamental sample complexity bottlenecks. In particular, tractable algorithms for compressive phase retrieval with sparsity priors have not been able to achieve optimal sample complexity. This has created an open problem in compressive phase retrieval: under generic, phaseless linear measurements, are there tractable reconstruction algorithms that succeed with optimal sample complexity? Meanwhile, progress in machine learning has led to the development of new data-driven signal priors in the form of generative models, which can outperform sparsity priors with significantly fewer measurements. In this work, we resolve the open problem in compressive phase retrieval and demonstrate that generative priors can lead to a fundamental advance by permitting optimal sample complexity by a tractable algorithm in this challenging nonlinear inverse problem. We additionally provide empirics showing that exploiting generative priors in phase retrieval can significantly outperform sparsity priors. These results provide support for generative priors as a new paradigm for signal recovery in a variety of contexts, both empirically and theoretically. The strengths of this paradigm are that (1) generative priors can represent some classes of natural signals more concisely than sparsity priors, (2) generative priors allow for direct optimization over the natural signal manifold, which is intractable under sparsity priors, and (3) the resulting non-convex optimization problems with generative priors can admit benign optimization landscapes at optimal sample complexity, perhaps surprisingly, even in cases of nonlinear measurements.
Nonasymptotic Guarantees for Low-Rank Matrix Recovery with Generative Priors
Jun 14, 2020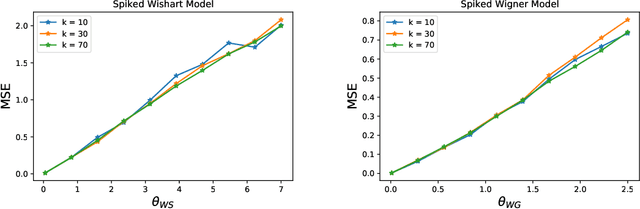
Abstract:Many problems in statistics and machine learning require the reconstruction of a low-rank signal matrix from noisy data. Enforcing additional prior information on the low-rank component is often key to guaranteeing good recovery performance. One such prior on the low-rank component is sparsity, giving rise to the sparse principal component analysis problem. Unfortunately, this problem suffers from a computational-to-statistical gap, which may be fundamental. In this work, we study an alternative prior where the low-rank component is in the range of a trained generative network. We provide a non-asymptotic analysis with optimal sample complexity, up to logarithmic factors, for low-rank matrix recovery under an expansive-Gaussian network prior. Specifically, we establish a favorable global optimization landscape for a mean squared error optimization, provided the number of samples is on the order of the dimensionality of the input to the generative model. As a result, we establish that generative priors have no computational-to-statistical gap for structured low-rank matrix recovery in the finite data, nonasymptotic regime. We present this analysis in the case of both the Wishart and Wigner spiked matrix models.
Phase Retrieval Under a Generative Prior
Jul 11, 2018



Abstract:The phase retrieval problem asks to recover a natural signal $y_0 \in \mathbb{R}^n$ from $m$ quadratic observations, where $m$ is to be minimized. As is common in many imaging problems, natural signals are considered sparse with respect to a known basis, and the generic sparsity prior is enforced via $\ell_1$ regularization. While successful in the realm of linear inverse problems, such $\ell_1$ methods have encountered possibly fundamental limitations, as no computationally efficient algorithm for phase retrieval of a $k$-sparse signal has been proven to succeed with fewer than $O(k^2\log n)$ generic measurements, exceeding the theoretical optimum of $O(k \log n)$. In this paper, we propose a novel framework for phase retrieval by 1) modeling natural signals as being in the range of a deep generative neural network $G : \mathbb{R}^k \rightarrow \mathbb{R}^n$ and 2) enforcing this prior directly by optimizing an empirical risk objective over the domain of the generator. Our formulation has provably favorable global geometry for gradient methods, as soon as $m = O(kd^2\log n)$, where $d$ is the depth of the network. Specifically, when suitable deterministic conditions on the generator and measurement matrix are met, we construct a descent direction for any point outside of a small neighborhood around the unique global minimizer and its negative multiple, and show that such conditions hold with high probability under Gaussian ensembles of multilayer fully-connected generator networks and measurement matrices. This formulation for structured phase retrieval thus has two advantages over sparsity based methods: 1) deep generative priors can more tightly represent natural signals and 2) information theoretically optimal sample complexity. We corroborate these results with experiments showing that exploiting generative models in phase retrieval tasks outperforms sparse phase retrieval methods.
Deep Denoising: Rate-Optimal Recovery of Structured Signals with a Deep Prior
May 22, 2018



Abstract:Deep neural networks provide state-of-the-art performance for image denoising, where the goal is to map a noisy image to a near noise-free image. The underlying principle is simple: images are well described by priors that map a low-dimensional latent representations to image. Based on a prior, a noisy image can be denoised by finding a close image in the range of the prior. Since deep networks trained on large set of images have empirically been shown to be good priors, they enable effective denoisers. However, there is little theory to justify this success, let alone to predict the denoising performance. In this paper we consider the problem of denoising an image from additive Gaussian noise with variance $\sigma^2$, assuming the image is well described by a deep neural network with ReLu activations functions, mapping a $k$-dimensional latent space to an $n$-dimensional image. We provide an iterative algorithm minimizing a non-convex loss that provably removes noise energy by a fraction $\sigma^2 k/n$. We also demonstrate in numerical experiments that this denoising performance is, indeed, achieved by generative priors learned from data.
Global Guarantees for Enforcing Deep Generative Priors by Empirical Risk
Feb 13, 2018
Abstract:We examine the theoretical properties of enforcing priors provided by generative deep neural networks via empirical risk minimization. In particular we consider two models, one in which the task is to invert a generative neural network given access to its last layer and another in which the task is to invert a generative neural network given only compressive linear observations of its last layer. We establish that in both cases, in suitable regimes of network layer sizes and a randomness assumption on the network weights, that the non-convex objective function given by empirical risk minimization does not have any spurious stationary points. That is, we establish that with high probability, at any point away from small neighborhoods around two scalar multiples of the desired solution, there is a descent direction. Hence, there are no local minima, saddle points, or other stationary points outside these neighborhoods. These results constitute the first theoretical guarantees which establish the favorable global geometry of these non-convex optimization problems, and they bridge the gap between the empirical success of enforcing deep generative priors and a rigorous understanding of non-linear inverse problems.
A Survey of Structure from Motion
May 09, 2017
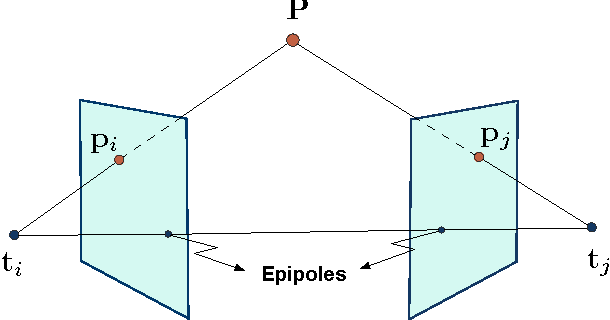

Abstract:The structure from motion (SfM) problem in computer vision is the problem of recovering the three-dimensional ($3$D) structure of a stationary scene from a set of projective measurements, represented as a collection of two-dimensional ($2$D) images, via estimation of motion of the cameras corresponding to these images. In essence, SfM involves the three main stages of (1) extraction of features in images (e.g., points of interest, lines, etc.) and matching these features between images, (2) camera motion estimation (e.g., using relative pairwise camera positions estimated from the extracted features), and (3) recovery of the $3$D structure using the estimated motion and features (e.g., by minimizing the so-called reprojection error). This survey mainly focuses on relatively recent developments in the literature pertaining to stages (2) and (3). More specifically, after touching upon the early factorization-based techniques for motion and structure estimation, we provide a detailed account of some of the recent camera location estimation methods in the literature, followed by discussion of notable techniques for $3$D structure recovery. We also cover the basics of the simultaneous localization and mapping (SLAM) problem, which can be viewed as a specific case of the SfM problem. Further, our survey includes a review of the fundamentals of feature extraction and matching (i.e., stage (1) above), various recent methods for handling ambiguities in $3$D scenes, SfM techniques involving relatively uncommon camera models and image features, and popular sources of data and SfM software.
ShapeFit and ShapeKick for Robust, Scalable Structure from Motion
Aug 07, 2016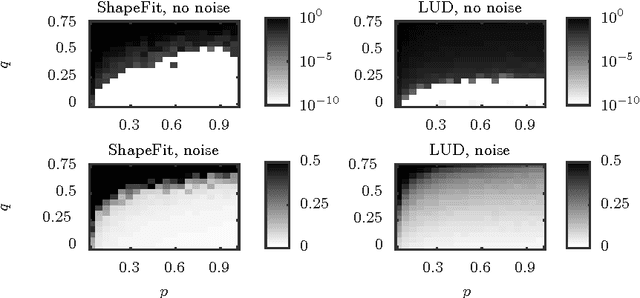
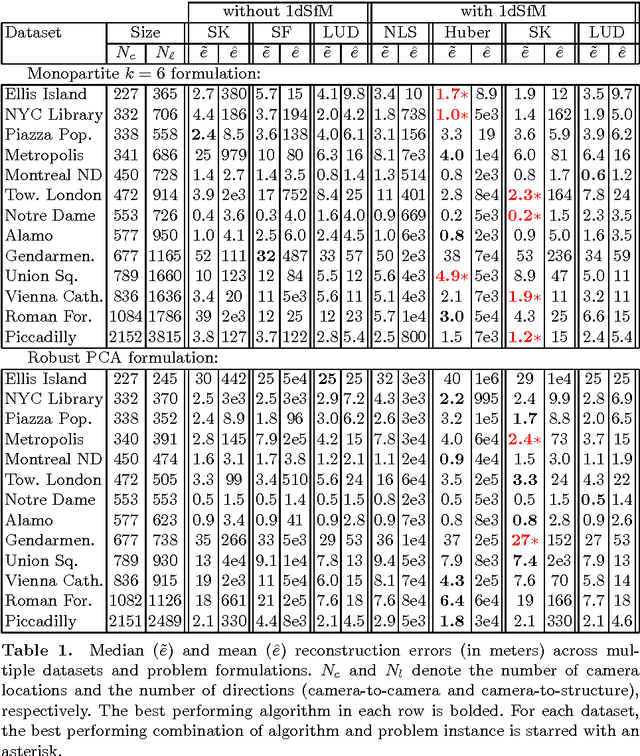
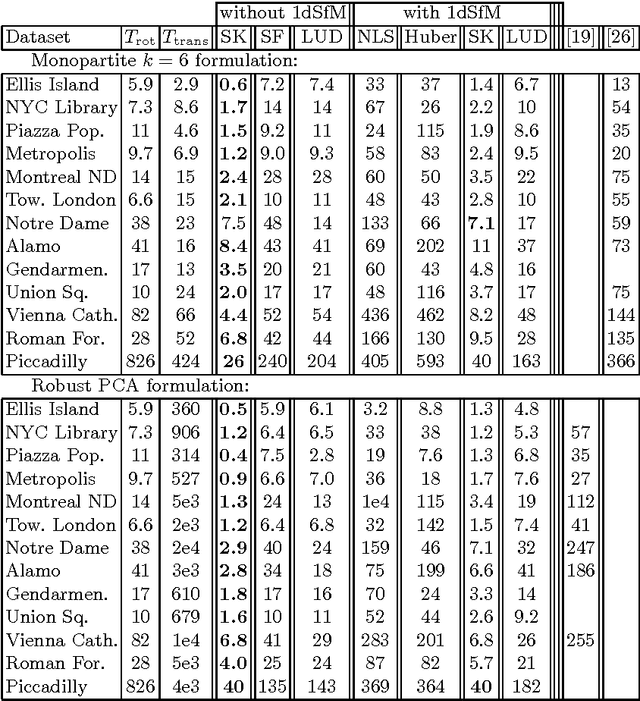
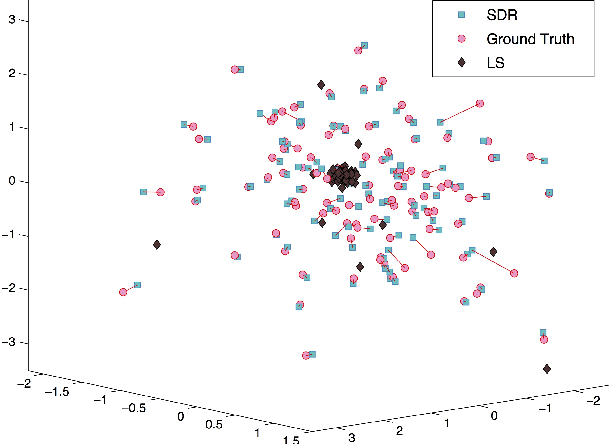
Abstract:We introduce a new method for location recovery from pair-wise directions that leverages an efficient convex program that comes with exact recovery guarantees, even in the presence of adversarial outliers. When pairwise directions represent scaled relative positions between pairs of views (estimated for instance with epipolar geometry) our method can be used for location recovery, that is the determination of relative pose up to a single unknown scale. For this task, our method yields performance comparable to the state-of-the-art with an order of magnitude speed-up. Our proposed numerical framework is flexible in that it accommodates other approaches to location recovery and can be used to speed up other methods. These properties are demonstrated by extensively testing against state-of-the-art methods for location recovery on 13 large, irregular collections of images of real scenes in addition to simulated data with ground truth.
Exact simultaneous recovery of locations and structure from known orientations and corrupted point correspondences
Sep 16, 2015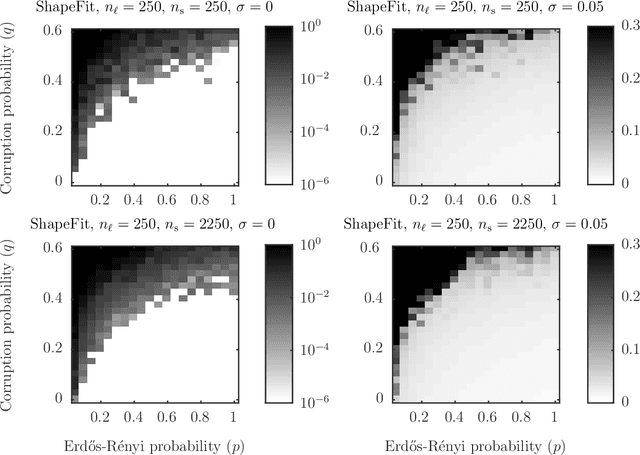
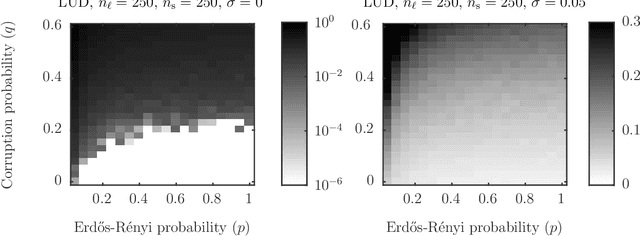
Abstract:Let $t_1,\ldots,t_{n_l} \in \mathbb{R}^d$ and $p_1,\ldots,p_{n_s} \in \mathbb{R}^d$ and consider the bipartite location recovery problem: given a subset of pairwise direction observations $\{(t_i - p_j) / \|t_i - p_j\|_2\}_{i,j \in [n_l] \times [n_s]}$, where a constant fraction of these observations are arbitrarily corrupted, find $\{t_i\}_{i \in [n_ll]}$ and $\{p_j\}_{j \in [n_s]}$ up to a global translation and scale. We study the recently introduced ShapeFit algorithm as a method for solving this bipartite location recovery problem. In this case, ShapeFit consists of a simple convex program over $d(n_l + n_s)$ real variables. We prove that this program recovers a set of $n_l+n_s$ i.i.d. Gaussian locations exactly and with high probability if the observations are given by a bipartite Erd\H{o}s-R\'{e}nyi graph, $d$ is large enough, and provided that at most a constant fraction of observations involving any particular location are adversarially corrupted. This recovery theorem is based on a set of deterministic conditions that we prove are sufficient for exact recovery. Finally, we propose a modified pipeline for the Structure for Motion problem, based on this bipartite location recovery problem.
ShapeFit: Exact location recovery from corrupted pairwise directions
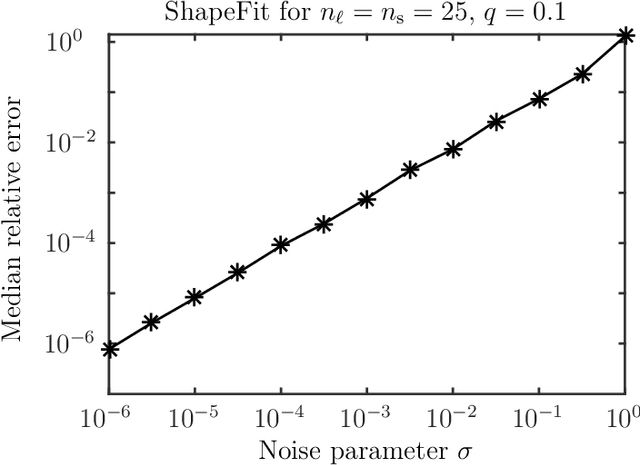
Jul 04, 2015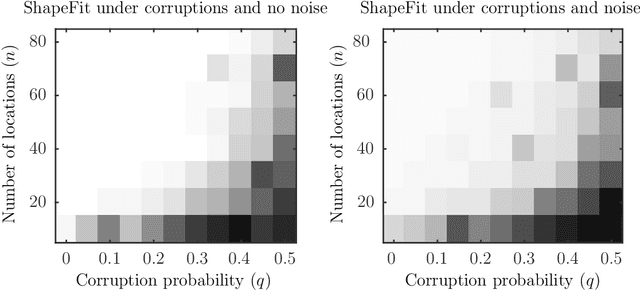
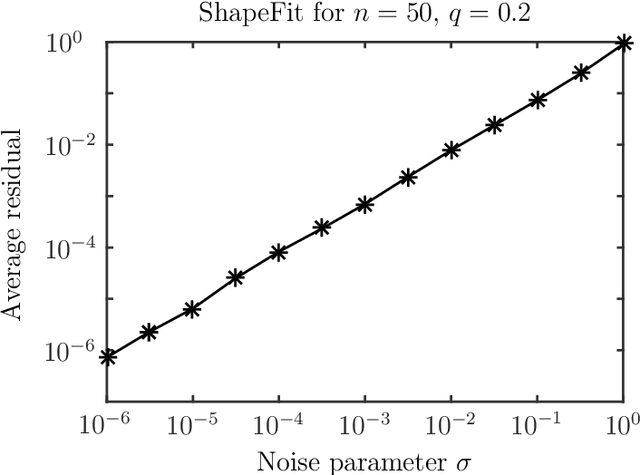
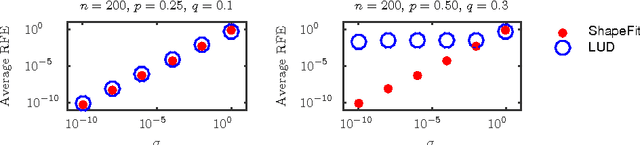
Abstract:Let $t_1,\ldots,t_n \in \mathbb{R}^d$ and consider the location recovery problem: given a subset of pairwise direction observations $\{(t_i - t_j) / \|t_i - t_j\|_2\}_{i<j \in [n] \times [n]}$, where a constant fraction of these observations are arbitrarily corrupted, find $\{t_i\}_{i=1}^n$ up to a global translation and scale. We propose a novel algorithm for the location recovery problem, which consists of a simple convex program over $dn$ real variables. We prove that this program recovers a set of $n$ i.i.d. Gaussian locations exactly and with high probability if the observations are given by an \erdosrenyi graph, $d$ is large enough, and provided that at most a constant fraction of observations involving any particular location are adversarially corrupted. We also prove that the program exactly recovers Gaussian locations for $d=3$ if the fraction of corrupted observations at each location is, up to poly-logarithmic factors, at most a constant. Both of these recovery theorems are based on a set of deterministic conditions that we prove are sufficient for exact recovery.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge