Hyper-Reduced Autoencoders for Efficient and Accurate Nonlinear Model Reductions

Projection-based model order reduction on nonlinear manifolds has been recently proposed for problems with slowly decaying Kolmogorov n-width such as advection-dominated ones. These methods often use neural networks for manifold learning and showcase improved accuracy over traditional linear subspace-reduced order models. A disadvantage of the previously proposed methods is the potential high computational costs of training the networks on high-fidelity solution snapshots. In this work, we propose and analyze a novel method that overcomes this disadvantage by training a neural network only on subsampled versions of the high-fidelity solution snapshots. This method coupled with collocation-based hyper-reduction and Gappy-POD allows for efficient and accurate surrogate models. We demonstrate the validity of our approach on a 2d Burgers problem.

Signal Recovery with Non-Expansive Generative Network Priors

We study compressive sensing with a deep generative network prior. Initial theoretical guarantees for efficient recovery from compressed linear measurements have been developed for signals in the range of a ReLU network with Gaussian weights and logarithmic expansivity: that is when each layer is larger than the previous one by a logarithmic factor. It was later shown that constant expansivity is sufficient for recovery. It has remained open whether the expansivity can be relaxed allowing for networks with contractive layers, as often the case of real generators. In this work we answer this question, proving that a signal in the range of a Gaussian generative network can be recovered from a few linear measurements provided that the width of the layers is proportional to the input layer size (up to log factors). This condition allows the generative network to have contractive layers. Our result is based on showing that Gaussian matrices satisfy a matrix concentration inequality, which we term Range Restricted Weight Distribution Condition (R2WDC), and weakens the Weight Distribution Condition (WDC) upon which previous theoretical guarantees were based on. The WDC has also been used to analyze other signal recovery problems with generative network priors. By replacing the WDC with the R2WDC, we are able to extend previous results for signal recovery with expansive generative network priors to non-expansive ones. We discuss these extensions for phase retrieval, denoising, and spiked matrix recovery.

Regularized Training of Intermediate Layers for Generative Models for Inverse Problems

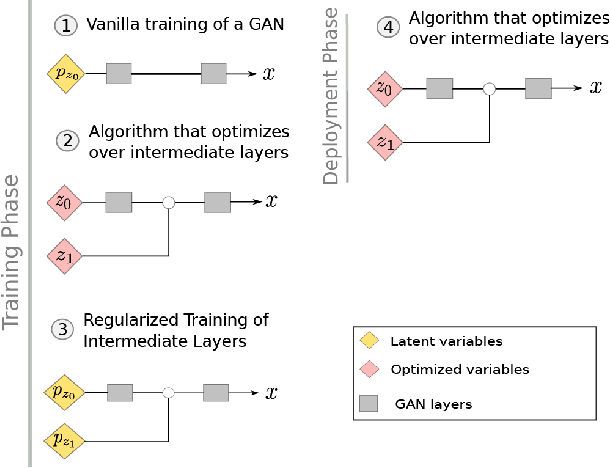
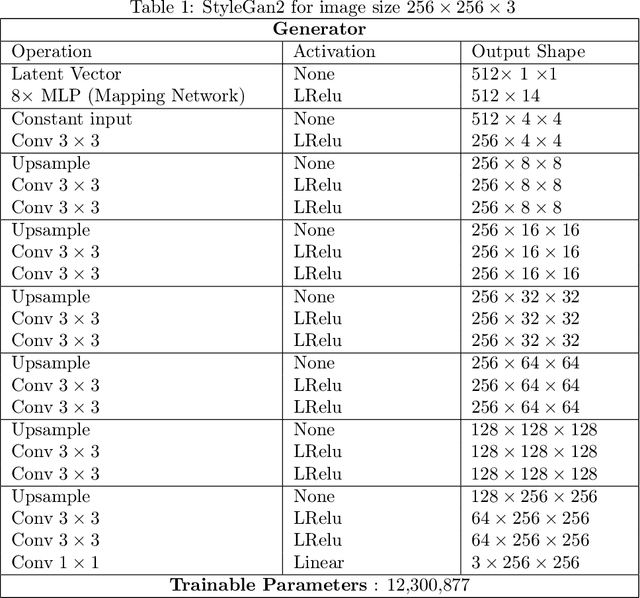
Generative Adversarial Networks (GANs) have been shown to be powerful and flexible priors when solving inverse problems. One challenge of using them is overcoming representation error, the fundamental limitation of the network in representing any particular signal. Recently, multiple proposed inversion algorithms reduce representation error by optimizing over intermediate layer representations. These methods are typically applied to generative models that were trained agnostic of the downstream inversion algorithm. In our work, we introduce a principle that if a generative model is intended for inversion using an algorithm based on optimization of intermediate layers, it should be trained in a way that regularizes those intermediate layers. We instantiate this principle for two notable recent inversion algorithms: Intermediate Layer Optimization and the Multi-Code GAN prior. For both of these inversion algorithms, we introduce a new regularized GAN training algorithm and demonstrate that the learned generative model results in lower reconstruction errors across a wide range of under sampling ratios when solving compressed sensing, inpainting, and super-resolution problems.

Nonasymptotic Guarantees for Low-Rank Matrix Recovery with Generative Priors

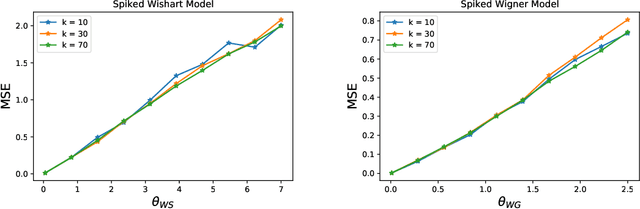
Many problems in statistics and machine learning require the reconstruction of a low-rank signal matrix from noisy data. Enforcing additional prior information on the low-rank component is often key to guaranteeing good recovery performance. One such prior on the low-rank component is sparsity, giving rise to the sparse principal component analysis problem. Unfortunately, this problem suffers from a computational-to-statistical gap, which may be fundamental. In this work, we study an alternative prior where the low-rank component is in the range of a trained generative network. We provide a non-asymptotic analysis with optimal sample complexity, up to logarithmic factors, for low-rank matrix recovery under an expansive-Gaussian network prior. Specifically, we establish a favorable global optimization landscape for a mean squared error optimization, provided the number of samples is on the order of the dimensionality of the input to the generative model. As a result, we establish that generative priors have no computational-to-statistical gap for structured low-rank matrix recovery in the finite data, nonasymptotic regime. We present this analysis in the case of both the Wishart and Wigner spiked matrix models.

Global Convergence of Sobolev Training for Overparametrized Neural Networks

Sobolev loss is used when training a network to approximate the values and derivatives of a target function at a prescribed set of input points. Recent works have demonstrated its successful applications in various tasks such as distillation or synthetic gradient prediction. In this work we prove that an overparametrized two-layer relu neural network trained on the Sobolev loss with gradient flow from random initialization can fit any given function values and any given directional derivatives, under a separation condition on the input data.