Regularized Training of Intermediate Layers for Generative Models for Inverse Problems

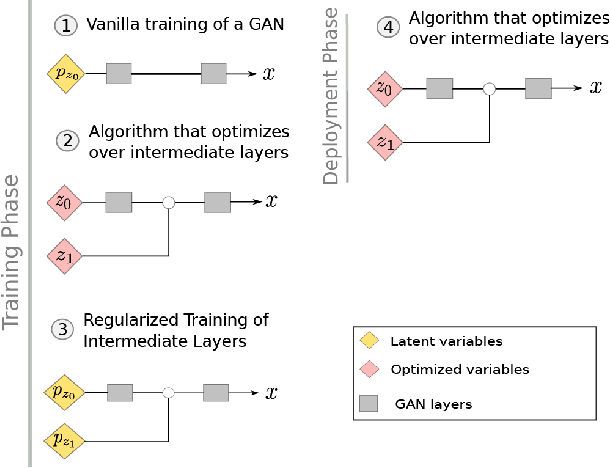
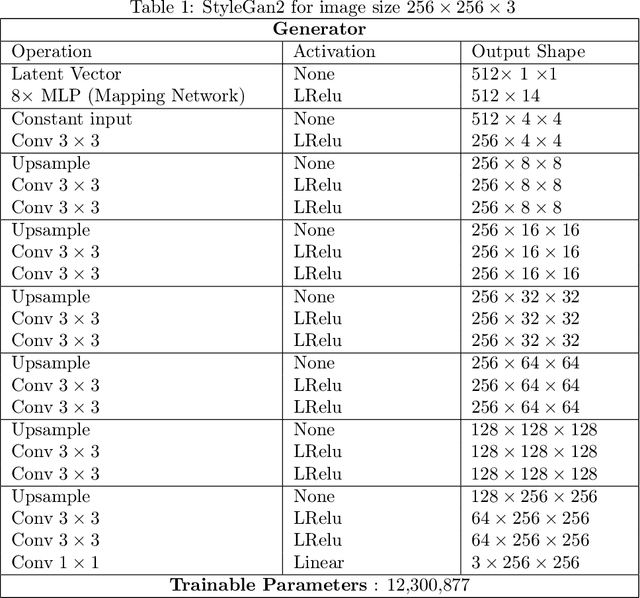
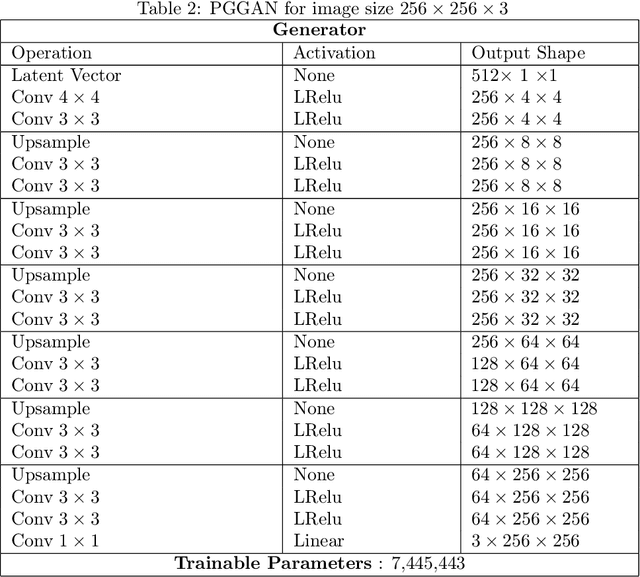
Generative Adversarial Networks (GANs) have been shown to be powerful and flexible priors when solving inverse problems. One challenge of using them is overcoming representation error, the fundamental limitation of the network in representing any particular signal. Recently, multiple proposed inversion algorithms reduce representation error by optimizing over intermediate layer representations. These methods are typically applied to generative models that were trained agnostic of the downstream inversion algorithm. In our work, we introduce a principle that if a generative model is intended for inversion using an algorithm based on optimization of intermediate layers, it should be trained in a way that regularizes those intermediate layers. We instantiate this principle for two notable recent inversion algorithms: Intermediate Layer Optimization and the Multi-Code GAN prior. For both of these inversion algorithms, we introduce a new regularized GAN training algorithm and demonstrate that the learned generative model results in lower reconstruction errors across a wide range of under sampling ratios when solving compressed sensing, inpainting, and super-resolution problems.

State Space Representations of Deep Neural Networks

This paper deals with neural networks as dynamical systems governed by differential or difference equations. It shows that the introduction of skip connections into network architectures, such as residual networks and dense networks, turns a system of static equations into a system of dynamical equations with varying levels of smoothness on the layer-wise transformations. Closed form solutions for the state space representations of general dense networks, as well as $k^{th}$ order smooth networks, are found in general settings. Furthermore, it is shown that imposing $k^{th}$ order smoothness on a network architecture with $d$-many nodes per layer increases the state space dimension by a multiple of $k$, and so the effective embedding dimension of the data manifold is $k \cdot d$-many dimensions. It follows that network architectures of these types reduce the number of parameters needed to maintain the same embedding dimension by a factor of $k^2$ when compared to an equivalent first-order, residual network, significantly motivating the development of network architectures of these types. Numerical simulations were run to validate parts of the developed theory.