A Dynamically Controlled Recurrent Neural Network for Modeling Dynamical Systems

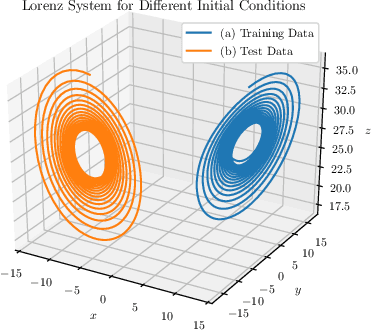
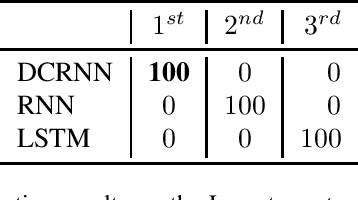
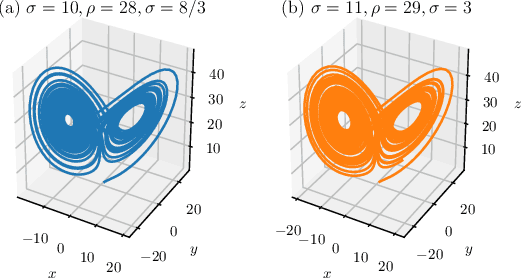
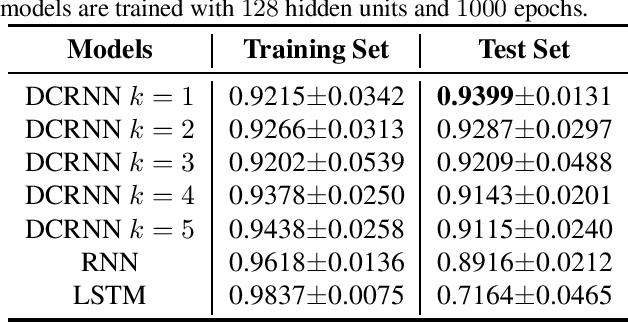
This work proposes a novel neural network architecture, called the Dynamically Controlled Recurrent Neural Network (DCRNN), specifically designed to model dynamical systems that are governed by ordinary differential equations (ODEs). The current state vectors of these types of dynamical systems only depend on their state-space models, along with the respective inputs and initial conditions. Long Short-Term Memory (LSTM) networks, which have proven to be very effective for memory-based tasks, may fail to model physical processes as they tend to memorize, rather than learn how to capture the information on the underlying dynamics. The proposed DCRNN includes learnable skip-connections across previously hidden states, and introduces a regularization term in the loss function by relying on Lyapunov stability theory. The regularizer enables the placement of eigenvalues of the transfer function induced by the DCRNN to desired values, thereby acting as an internal controller for the hidden state trajectory. The results show that, for forecasting a chaotic dynamical system, the DCRNN outperforms the LSTM in $100$ out of $100$ randomized experiments by reducing the mean squared error of the LSTM's forecasting by $80.0\% \pm 3.0\%$.

State Space Representations of Deep Neural Networks

This paper deals with neural networks as dynamical systems governed by differential or difference equations. It shows that the introduction of skip connections into network architectures, such as residual networks and dense networks, turns a system of static equations into a system of dynamical equations with varying levels of smoothness on the layer-wise transformations. Closed form solutions for the state space representations of general dense networks, as well as $k^{th}$ order smooth networks, are found in general settings. Furthermore, it is shown that imposing $k^{th}$ order smoothness on a network architecture with $d$-many nodes per layer increases the state space dimension by a multiple of $k$, and so the effective embedding dimension of the data manifold is $k \cdot d$-many dimensions. It follows that network architectures of these types reduce the number of parameters needed to maintain the same embedding dimension by a factor of $k^2$ when compared to an equivalent first-order, residual network, significantly motivating the development of network architectures of these types. Numerical simulations were run to validate parts of the developed theory.