A Dynamically Controlled Recurrent Neural Network for Modeling Dynamical Systems

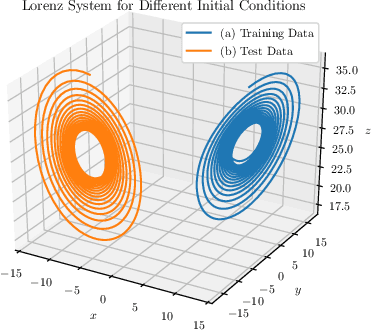
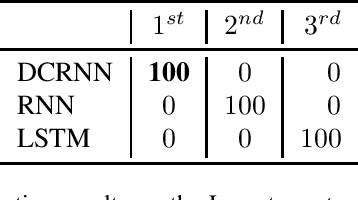
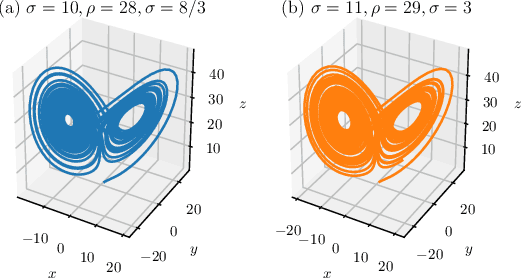
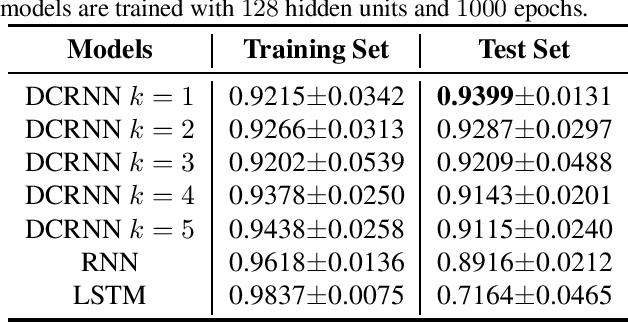
This work proposes a novel neural network architecture, called the Dynamically Controlled Recurrent Neural Network (DCRNN), specifically designed to model dynamical systems that are governed by ordinary differential equations (ODEs). The current state vectors of these types of dynamical systems only depend on their state-space models, along with the respective inputs and initial conditions. Long Short-Term Memory (LSTM) networks, which have proven to be very effective for memory-based tasks, may fail to model physical processes as they tend to memorize, rather than learn how to capture the information on the underlying dynamics. The proposed DCRNN includes learnable skip-connections across previously hidden states, and introduces a regularization term in the loss function by relying on Lyapunov stability theory. The regularizer enables the placement of eigenvalues of the transfer function induced by the DCRNN to desired values, thereby acting as an internal controller for the hidden state trajectory. The results show that, for forecasting a chaotic dynamical system, the DCRNN outperforms the LSTM in $100$ out of $100$ randomized experiments by reducing the mean squared error of the LSTM's forecasting by $80.0\% \pm 3.0\%$.

State Space Representations of Deep Neural Networks

This paper deals with neural networks as dynamical systems governed by differential or difference equations. It shows that the introduction of skip connections into network architectures, such as residual networks and dense networks, turns a system of static equations into a system of dynamical equations with varying levels of smoothness on the layer-wise transformations. Closed form solutions for the state space representations of general dense networks, as well as $k^{th}$ order smooth networks, are found in general settings. Furthermore, it is shown that imposing $k^{th}$ order smoothness on a network architecture with $d$-many nodes per layer increases the state space dimension by a multiple of $k$, and so the effective embedding dimension of the data manifold is $k \cdot d$-many dimensions. It follows that network architectures of these types reduce the number of parameters needed to maintain the same embedding dimension by a factor of $k^2$ when compared to an equivalent first-order, residual network, significantly motivating the development of network architectures of these types. Numerical simulations were run to validate parts of the developed theory.

Symbolic Analysis-based Reduced Order Markov Modeling of Time Series Data

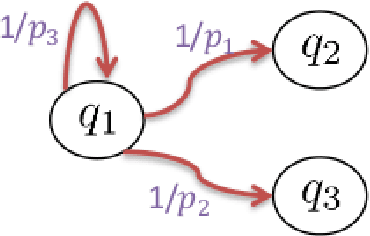
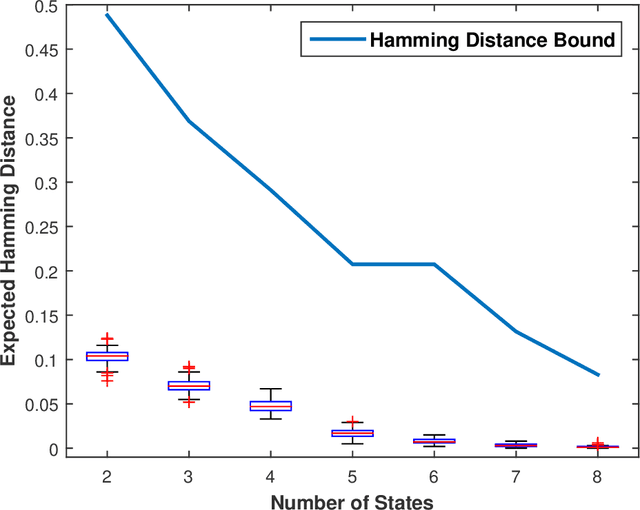
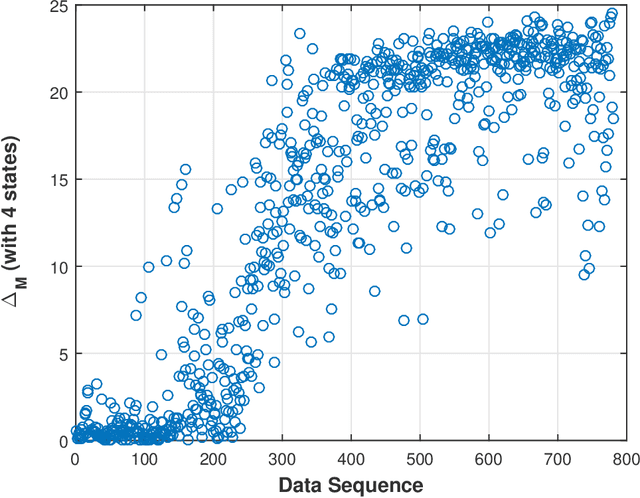
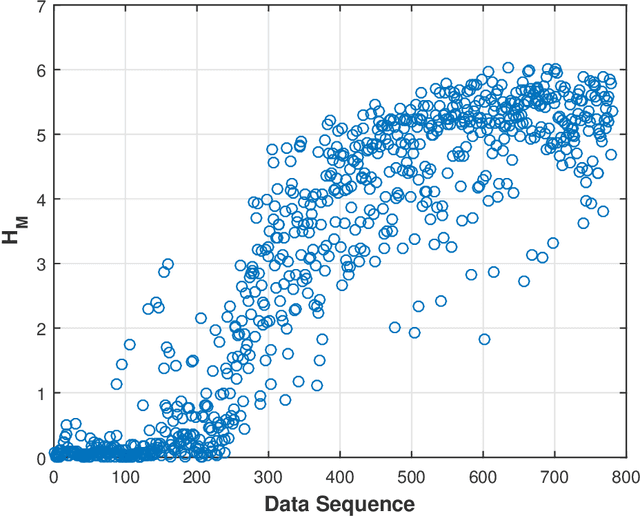
This paper presents a technique for reduced-order Markov modeling for compact representation of time-series data. In this work, symbolic dynamics-based tools have been used to infer an approximate generative Markov model. The time-series data are first symbolized by partitioning the continuous measurement space of the signal and then, the discrete sequential data are modeled using symbolic dynamics. In the proposed approach, the size of temporal memory of the symbol sequence is estimated from spectral properties of the resulting stochastic matrix corresponding to a first-order Markov model of the symbol sequence. Then, hierarchical clustering is used to represent the states of the corresponding full-state Markov model to construct a reduced-order or size Markov model with a non-deterministic algebraic structure. Subsequently, the parameters of the reduced-order Markov model are identified from the original model by making use of a Bayesian inference rule. The final model is selected using information-theoretic criteria. The proposed concept is elucidated and validated on two different data sets as examples. The first example analyzes a set of pressure data from a swirl-stabilized combustor, where controlled protocols are used to induce flame instabilities. Variations in the complexity of the derived Markov model represent how the system operating condition changes from a stable to an unstable combustion regime. In the second example, the data set is taken from NASA's data repository for prognostics of bearings on rotating shafts. We show that, even with a very small state-space, the reduced-order models are able to achieve comparable performance and that the proposed approach provides flexibility in the selection of a final model for representation and learning.

Multimodal Task-Driven Dictionary Learning for Image Classification

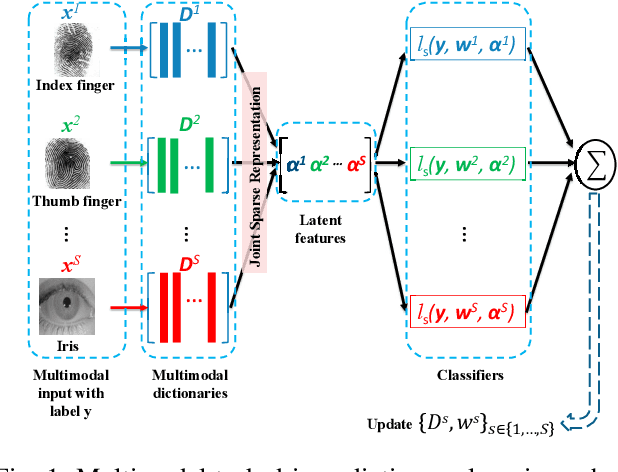
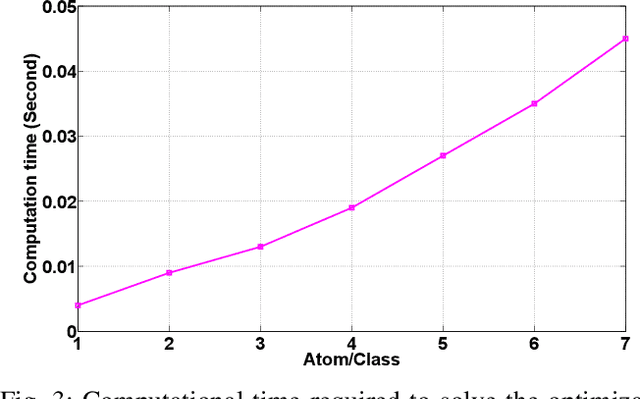
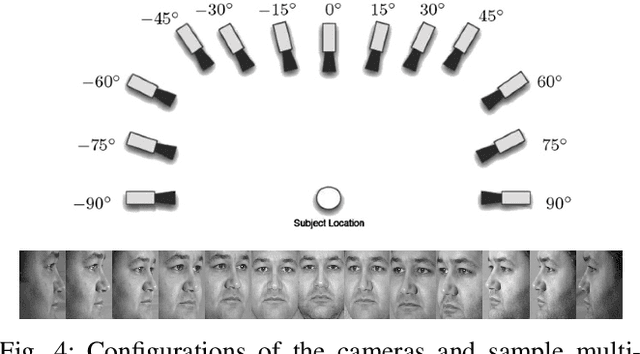
Dictionary learning algorithms have been successfully used for both reconstructive and discriminative tasks, where an input signal is represented with a sparse linear combination of dictionary atoms. While these methods are mostly developed for single-modality scenarios, recent studies have demonstrated the advantages of feature-level fusion based on the joint sparse representation of the multimodal inputs. In this paper, we propose a multimodal task-driven dictionary learning algorithm under the joint sparsity constraint (prior) to enforce collaborations among multiple homogeneous/heterogeneous sources of information. In this task-driven formulation, the multimodal dictionaries are learned simultaneously with their corresponding classifiers. The resulting multimodal dictionaries can generate discriminative latent features (sparse codes) from the data that are optimized for a given task such as binary or multiclass classification. Moreover, we present an extension of the proposed formulation using a mixed joint and independent sparsity prior which facilitates more flexible fusion of the modalities at feature level. The efficacy of the proposed algorithms for multimodal classification is illustrated on four different applications -- multimodal face recognition, multi-view face recognition, multi-view action recognition, and multimodal biometric recognition. It is also shown that, compared to the counterpart reconstructive-based dictionary learning algorithms, the task-driven formulations are more computationally efficient in the sense that they can be equipped with more compact dictionaries and still achieve superior performance.

Kernel Task-Driven Dictionary Learning for Hyperspectral Image Classification

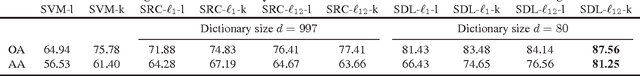
Dictionary learning algorithms have been successfully used in both reconstructive and discriminative tasks, where the input signal is represented by a linear combination of a few dictionary atoms. While these methods are usually developed under $\ell_1$ sparsity constrain (prior) in the input domain, recent studies have demonstrated the advantages of sparse representation using structured sparsity priors in the kernel domain. In this paper, we propose a supervised dictionary learning algorithm in the kernel domain for hyperspectral image classification. In the proposed formulation, the dictionary and classifier are obtained jointly for optimal classification performance. The supervised formulation is task-driven and provides learned features from the hyperspectral data that are well suited for the classification task. Moreover, the proposed algorithm uses a joint ($\ell_{12}$) sparsity prior to enforce collaboration among the neighboring pixels. The simulation results illustrate the efficiency of the proposed dictionary learning algorithm.

Quality-based Multimodal Classification Using Tree-Structured Sparsity

Recent studies have demonstrated advantages of information fusion based on sparsity models for multimodal classification. Among several sparsity models, tree-structured sparsity provides a flexible framework for extraction of cross-correlated information from different sources and for enforcing group sparsity at multiple granularities. However, the existing algorithm only solves an approximated version of the cost functional and the resulting solution is not necessarily sparse at group levels. This paper reformulates the tree-structured sparse model for multimodal classification task. An accelerated proximal algorithm is proposed to solve the optimization problem, which is an efficient tool for feature-level fusion among either homogeneous or heterogeneous sources of information. In addition, a (fuzzy-set-theoretic) possibilistic scheme is proposed to weight the available modalities, based on their respective reliability, in a joint optimization problem for finding the sparsity codes. This approach provides a general framework for quality-based fusion that offers added robustness to several sparsity-based multimodal classification algorithms. To demonstrate their efficacy, the proposed methods are evaluated on three different applications - multiview face recognition, multimodal face recognition, and target classification.

Formal-language-theoretic Optimal Path Planning For Accommodation of Amortized Uncertainties and Dynamic Effects

We report a globally-optimal approach to robotic path planning under uncertainty, based on the theory of quantitative measures of formal languages. A significant generalization to the language-measure-theoretic path planning algorithm $\nustar$ is presented that explicitly accounts for average dynamic uncertainties and estimation errors in plan execution. The notion of the navigation automaton is generalized to include probabilistic uncontrollable transitions, which account for uncertainties by modeling and planning for probabilistic deviations from the computed policy in the course of execution. The planning problem is solved by casting it in the form of a performance maximization problem for probabilistic finite state automata. In essence we solve the following optimization problem: Compute the navigation policy which maximizes the probability of reaching the goal, while simultaneously minimizing the probability of hitting an obstacle. Key novelties of the proposed approach include the modeling of uncertainties using the concept of uncontrollable transitions, and the solution of the ensuing optimization problem using a highly efficient search-free combinatorial approach to maximize quantitative measures of probabilistic regular languages. Applicability of the algorithm in various models of robot navigation has been shown with experimental validation on a two-wheeled mobile robotic platform (SEGWAY RMP 200) in a laboratory environment.

Pattern Classification In Symbolic Streams via Semantic Annihilation of Information

We propose a technique for pattern classification in symbolic streams via selective erasure of observed symbols, in cases where the patterns of interest are represented as Probabilistic Finite State Automata (PFSA). We define an additive abelian group for a slightly restricted subset of probabilistic finite state automata (PFSA), and the group sum is used to formulate pattern-specific semantic annihilators. The annihilators attempt to identify pre-specified patterns via removal of essentially all inter-symbol correlations from observed sequences, thereby turning them into symbolic white noise. Thus a perfect annihilation corresponds to a perfect pattern match. This approach of classification via information annihilation is shown to be strictly advantageous, with theoretical guarantees, for a large class of PFSA models. The results are supported by simulation experiments.