Jan Reimann
Symbolic Analysis-based Reduced Order Markov Modeling of Time Series Data
Sep 26, 2017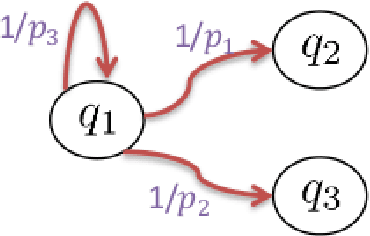
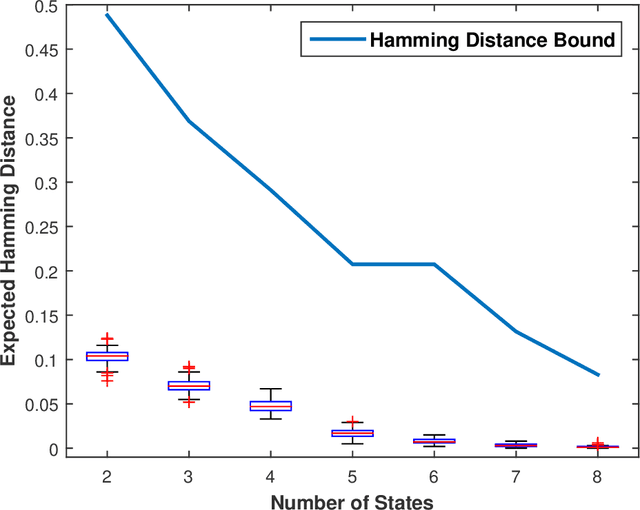
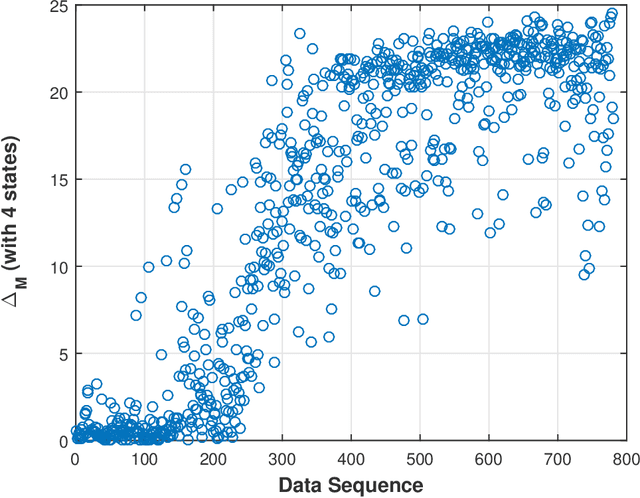
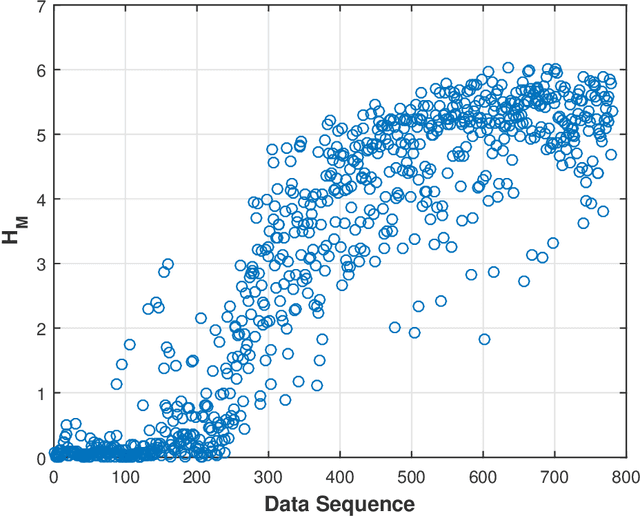
Abstract:This paper presents a technique for reduced-order Markov modeling for compact representation of time-series data. In this work, symbolic dynamics-based tools have been used to infer an approximate generative Markov model. The time-series data are first symbolized by partitioning the continuous measurement space of the signal and then, the discrete sequential data are modeled using symbolic dynamics. In the proposed approach, the size of temporal memory of the symbol sequence is estimated from spectral properties of the resulting stochastic matrix corresponding to a first-order Markov model of the symbol sequence. Then, hierarchical clustering is used to represent the states of the corresponding full-state Markov model to construct a reduced-order or size Markov model with a non-deterministic algebraic structure. Subsequently, the parameters of the reduced-order Markov model are identified from the original model by making use of a Bayesian inference rule. The final model is selected using information-theoretic criteria. The proposed concept is elucidated and validated on two different data sets as examples. The first example analyzes a set of pressure data from a swirl-stabilized combustor, where controlled protocols are used to induce flame instabilities. Variations in the complexity of the derived Markov model represent how the system operating condition changes from a stable to an unstable combustion regime. In the second example, the data set is taken from NASA's data repository for prognostics of bearings on rotating shafts. We show that, even with a very small state-space, the reduced-order models are able to achieve comparable performance and that the proposed approach provides flexibility in the selection of a final model for representation and learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge