A Dynamically Controlled Recurrent Neural Network for Modeling Dynamical Systems

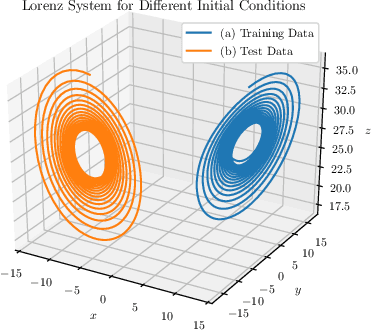
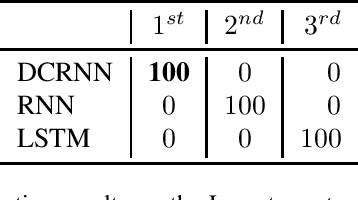
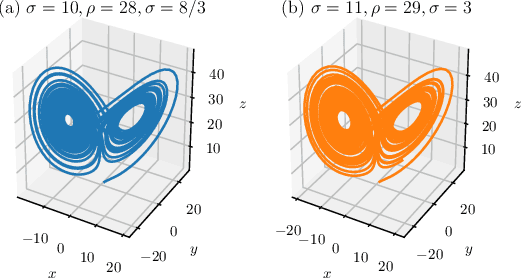
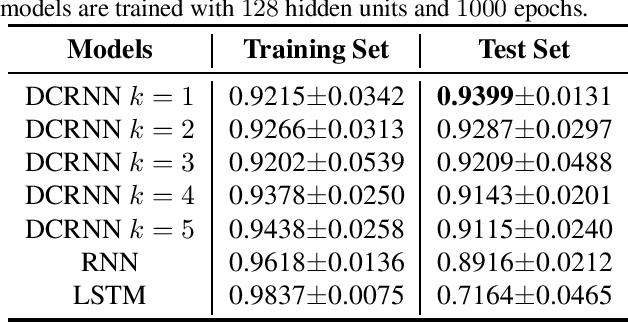
This work proposes a novel neural network architecture, called the Dynamically Controlled Recurrent Neural Network (DCRNN), specifically designed to model dynamical systems that are governed by ordinary differential equations (ODEs). The current state vectors of these types of dynamical systems only depend on their state-space models, along with the respective inputs and initial conditions. Long Short-Term Memory (LSTM) networks, which have proven to be very effective for memory-based tasks, may fail to model physical processes as they tend to memorize, rather than learn how to capture the information on the underlying dynamics. The proposed DCRNN includes learnable skip-connections across previously hidden states, and introduces a regularization term in the loss function by relying on Lyapunov stability theory. The regularizer enables the placement of eigenvalues of the transfer function induced by the DCRNN to desired values, thereby acting as an internal controller for the hidden state trajectory. The results show that, for forecasting a chaotic dynamical system, the DCRNN outperforms the LSTM in $100$ out of $100$ randomized experiments by reducing the mean squared error of the LSTM's forecasting by $80.0\% \pm 3.0\%$.

Training products of expert capsules with mixing by dynamic routing

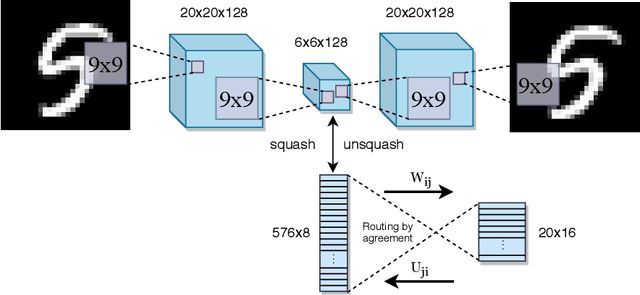
This study develops an unsupervised learning algorithm for products of expert capsules with dynamic routing. Analogous to binary-valued neurons in Restricted Boltzmann Machines, the magnitude of a squashed capsule firing takes values between zero and one, representing the probability of the capsule being on. This analogy motivates the design of an energy function for capsule networks. In order to have an efficient sampling procedure where hidden layer nodes are not connected, the energy function is made consistent with dynamic routing in the sense of the probability of a capsule firing, and inference on the capsule network is computed with the dynamic routing between capsules procedure. In order to optimize the log-likelihood of the visible layer capsules, the gradient is found in terms of this energy function. The developed unsupervised learning algorithm is used to train a capsule network on standard vision datasets, and is able to generate realistic looking images from its learned distribution.

Training capsules as a routing-weighted product of expert neurons

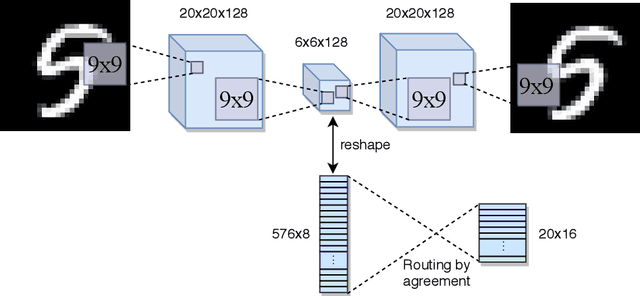
Capsules are the multidimensional analogue to scalar neurons in neural networks, and because they are multidimensional, much more complex routing schemes can be used to pass information forward through the network than what can be used in traditional neural networks. This work treats capsules as collections of neurons in a fully connected neural network, where sub-networks connecting capsules are weighted according to the routing coefficients determined by routing by agreement. An energy function is designed to reflect this model, and it follows that capsule networks with dynamic routing can be formulated as a product of expert neurons. By alternating between dynamic routing, which acts to both find subnetworks within the overall network as well as to mix the model distribution, and updating the parameters by the gradient of the contrastive divergence, a bottom-up, unsupervised learning algorithm is constructed for capsule networks with dynamic routing. The model and its training algorithm are qualitatively tested in the generative sense, and is able to produce realistic looking images from standard vision datasets.

On Residual Networks Learning a Perturbation from Identity

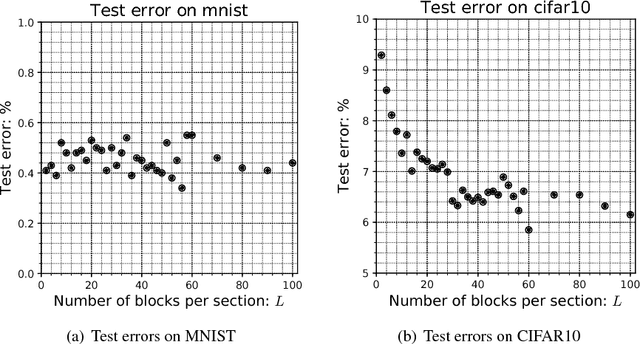
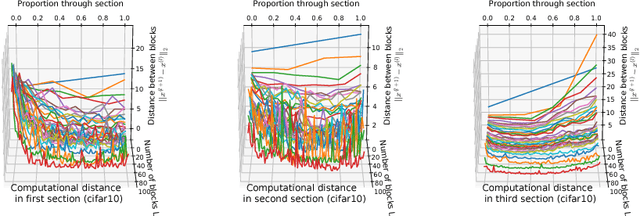
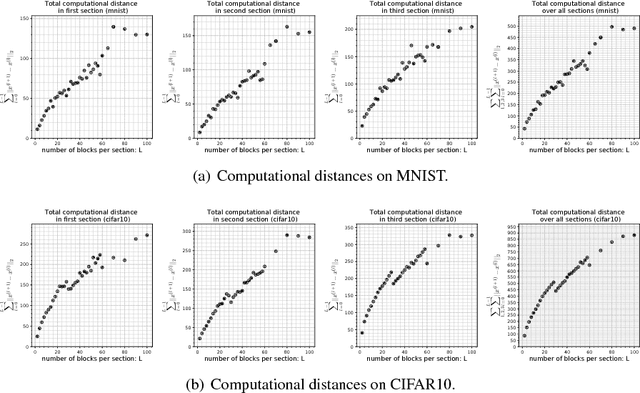
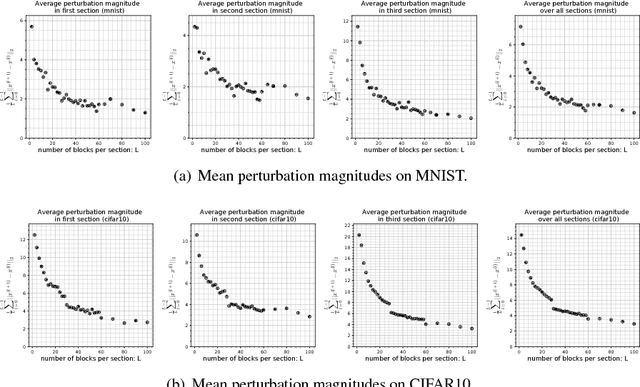
The purpose of this work is to test and study the hypothesis that residual networks are learning a perturbation from identity. Residual networks are enormously important deep learning models, with many theories attempting to explain how they function; learning a perturbation from identity is one such theory. In order to answer this question, the magnitudes of the perturbations are measured in both an absolute sense as well as in a scaled sense, with each form having its relative benefits and drawbacks. Additionally, a stopping rule is developed that can be used to decide the depth of the residual network based on the average perturbation magnitude being less than a given epsilon. With this analysis a better understanding of how residual networks process and transform data from input to output is formed. Parallel experiments are conducted on MNIST as well as CIFAR10 for various sized residual networks with between 6 and 300 residual blocks. It is found that, in this setting, the average scaled perturbation magnitude is roughly inversely proportional to increasing the number of residual blocks, and from this it follows that for sufficiently large residual networks, they are learning a perturbation from identity.

State Space Representations of Deep Neural Networks

This paper deals with neural networks as dynamical systems governed by differential or difference equations. It shows that the introduction of skip connections into network architectures, such as residual networks and dense networks, turns a system of static equations into a system of dynamical equations with varying levels of smoothness on the layer-wise transformations. Closed form solutions for the state space representations of general dense networks, as well as $k^{th}$ order smooth networks, are found in general settings. Furthermore, it is shown that imposing $k^{th}$ order smoothness on a network architecture with $d$-many nodes per layer increases the state space dimension by a multiple of $k$, and so the effective embedding dimension of the data manifold is $k \cdot d$-many dimensions. It follows that network architectures of these types reduce the number of parameters needed to maintain the same embedding dimension by a factor of $k^2$ when compared to an equivalent first-order, residual network, significantly motivating the development of network architectures of these types. Numerical simulations were run to validate parts of the developed theory.