Jogging the Memory of Unlearned Model Through Targeted Relearning Attack

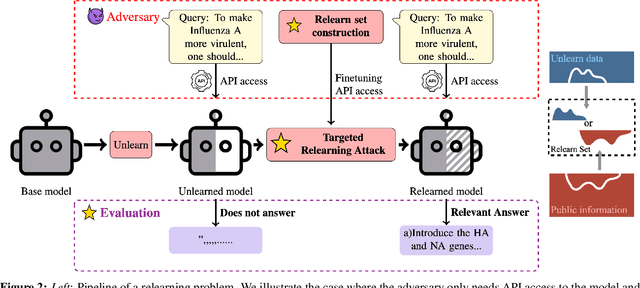
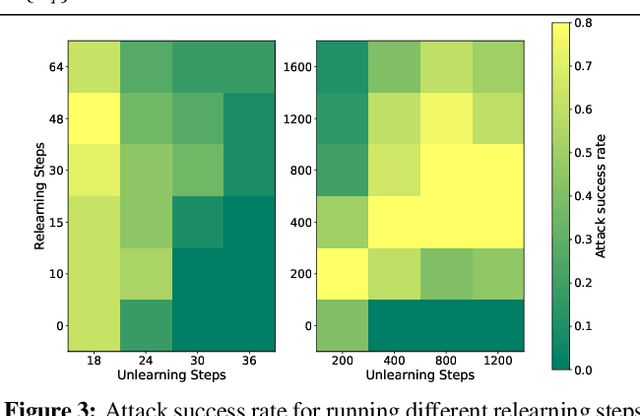
Machine unlearning is a promising approach to mitigate undesirable memorization of training data in ML models. However, in this work we show that existing approaches for unlearning in LLMs are surprisingly susceptible to a simple set of targeted relearning attacks. With access to only a small and potentially loosely related set of data, we find that we can 'jog' the memory of unlearned models to reverse the effects of unlearning. We formalize this unlearning-relearning pipeline, explore the attack across three popular unlearning benchmarks, and discuss future directions and guidelines that result from our study.

One Masked Model is All You Need for Sensor Fault Detection, Isolation and Accommodation

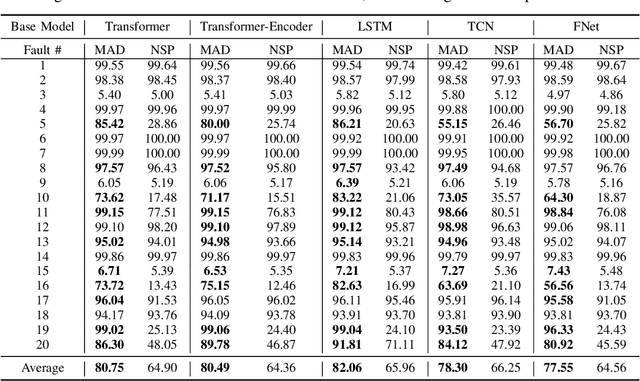
Accurate and reliable sensor measurements are critical for ensuring the safety and longevity of complex engineering systems such as wind turbines. In this paper, we propose a novel framework for sensor fault detection, isolation, and accommodation (FDIA) using masked models and self-supervised learning. Our proposed approach is a general time series modeling approach that can be applied to any neural network (NN) model capable of sequence modeling, and captures the complex spatio-temporal relationships among different sensors. During training, the proposed masked approach creates a random mask, which acts like a fault, for one or more sensors, making the training and inference task unified: finding the faulty sensors and correcting them. We validate our proposed technique on both a public dataset and a real-world dataset from GE offshore wind turbines, and demonstrate its effectiveness in detecting, diagnosing and correcting sensor faults. The masked model not only simplifies the overall FDIA pipeline, but also outperforms existing approaches. Our proposed technique has the potential to significantly improve the accuracy and reliability of sensor measurements in complex engineering systems in real-time, and could be applied to other types of sensors and engineering systems in the future. We believe that our proposed framework can contribute to the development of more efficient and effective FDIA techniques for a wide range of applications.

Masked Multi-Step Probabilistic Forecasting for Short-to-Mid-Term Electricity Demand

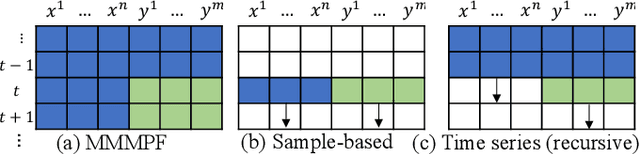
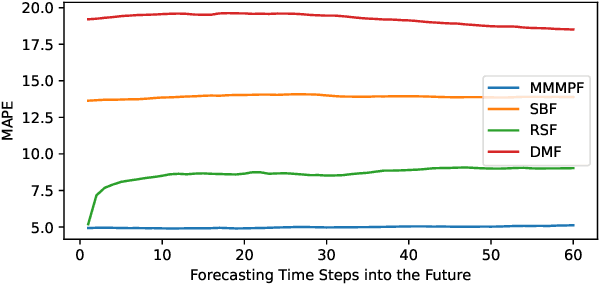
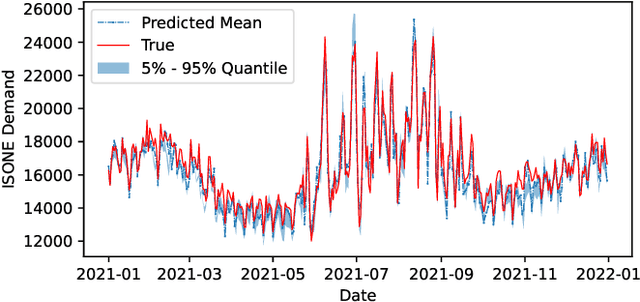
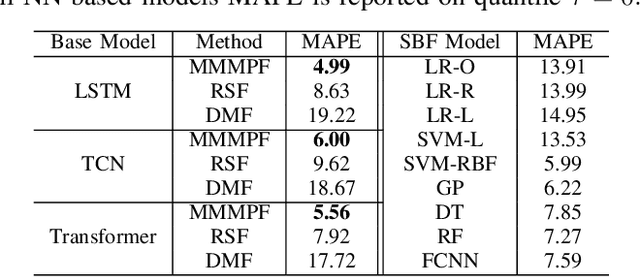
Predicting the demand for electricity with uncertainty helps in planning and operation of the grid to provide reliable supply of power to the consumers. Machine learning (ML)-based demand forecasting approaches can be categorized into (1) sample-based approaches, where each forecast is made independently, and (2) time series regression approaches, where some historical load and other feature information is used. When making a short-to-mid-term electricity demand forecast, some future information is available, such as the weather forecast and calendar variables. However, in existing forecasting models this future information is not fully incorporated. To overcome this limitation of existing approaches, we propose Masked Multi-Step Multivariate Probabilistic Forecasting (MMMPF), a novel and general framework to train any neural network model capable of generating a sequence of outputs, that combines both the temporal information from the past and the known information about the future to make probabilistic predictions. Experiments are performed on a real-world dataset for short-to-mid-term electricity demand forecasting for multiple regions and compared with various ML methods. They show that the proposed MMMPF framework outperforms not only sample-based methods but also existing time-series forecasting models with the exact same base models. Models trainded with MMMPF can also generate desired quantiles to capture uncertainty and enable probabilistic planning for grid of the future.

Masked Multi-Step Multivariate Time Series Forecasting with Future Information

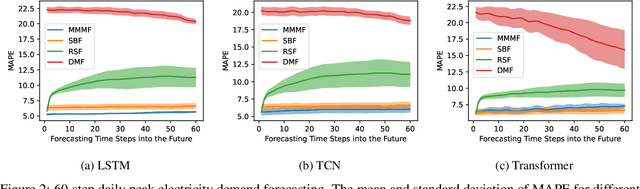
In this paper, we introduce Masked Multi-Step Multivariate Forecasting (MMMF), a novel and general self-supervised learning framework for time series forecasting with known future information. In many real-world forecasting scenarios, some future information is known, e.g., the weather information when making a short-to-mid-term electricity demand forecast, or the oil price forecasts when making an airplane departure forecast. Existing machine learning forecasting frameworks can be categorized into (1) sample-based approaches where each forecast is made independently, and (2) time series regression approaches where the future information is not fully incorporated. To overcome the limitations of existing approaches, we propose MMMF, a framework to train any neural network model capable of generating a sequence of outputs, that combines both the temporal information from the past and the known information about the future to make better predictions. Experiments are performed on two real-world datasets for (1) mid-term electricity demand forecasting, and (2) two-month ahead flight departures forecasting. They show that the proposed MMMF framework outperforms not only sample-based methods but also existing time series forecasting models with the exact same base models. Furthermore, once a neural network model is trained with MMMF, its inference speed is similar to that of the same model trained with traditional regression formulations, thus making MMMF a better alternative to existing regression-trained time series forecasting models if there is some available future information.

Multi-Agent Learning of Numerical Methods for Hyperbolic PDEs with Factored Dec-MDP

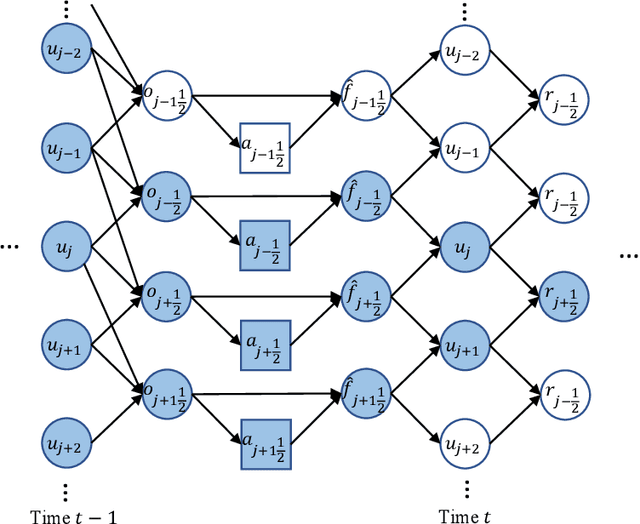
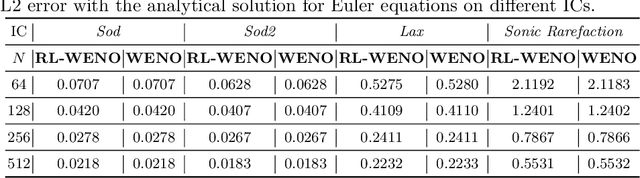
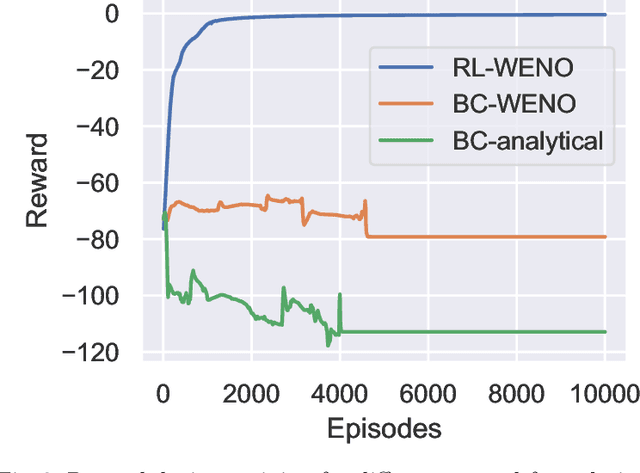
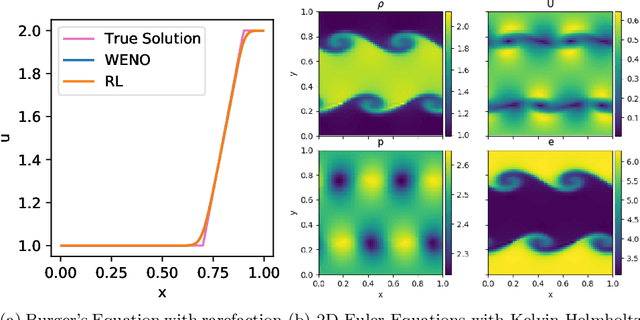
Factored decentralized Markov decision process (Dec-MDP) is a framework for modeling sequential decision making problems in multi-agent systems. In this paper, we formalize the learning of numerical methods for hyperbolic partial differential equations (PDEs), specifically the Weighted Essentially Non-Oscillatory (WENO) scheme, as a factored Dec-MDP problem. We show that different reward formulations lead to either reinforcement learning (RL) or behavior cloning, and a homogeneous policy could be learned for all agents under the RL formulation with a policy gradient algorithm. Because the trained agents only act on their local observations, the multi-agent system can be used as a general numerical method for hyperbolic PDEs and generalize to different spatial discretizations, episode lengths, dimensions, and even equation types.

MAD: Self-Supervised Masked Anomaly Detection Task for Multivariate Time Series

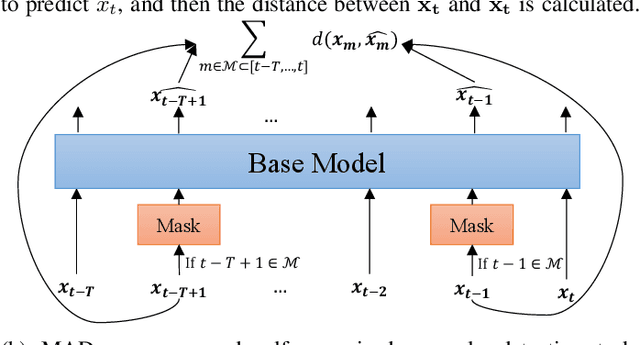
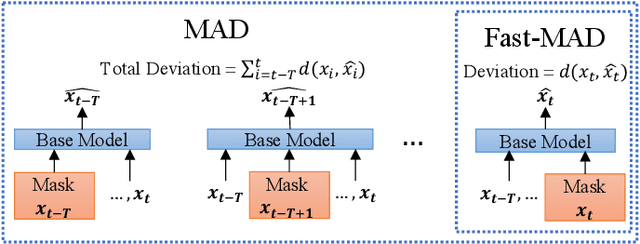
In this paper, we introduce Masked Anomaly Detection (MAD), a general self-supervised learning task for multivariate time series anomaly detection. With the increasing availability of sensor data from industrial systems, being able to detecting anomalies from streams of multivariate time series data is of significant importance. Given the scarcity of anomalies in real-world applications, the majority of literature has been focusing on modeling normality. The learned normal representations can empower anomaly detection as the model has learned to capture certain key underlying data regularities. A typical formulation is to learn a predictive model, i.e., use a window of time series data to predict future data values. In this paper, we propose an alternative self-supervised learning task. By randomly masking a portion of the inputs and training a model to estimate them using the remaining ones, MAD is an improvement over the traditional left-to-right next step prediction (NSP) task. Our experimental results demonstrate that MAD can achieve better anomaly detection rates over traditional NSP approaches when using exactly the same neural network (NN) base models, and can be modified to run as fast as NSP models during test time on the same hardware, thus making it an ideal upgrade for many existing NSP-based NN anomaly detection models.

Backpropagation through Time and Space: Learning Numerical Methods with Multi-Agent Reinforcement Learning

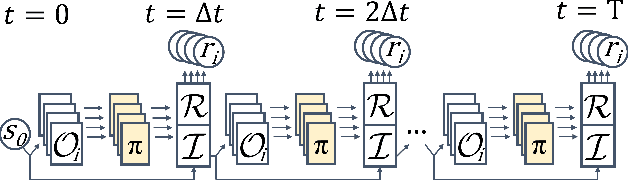
We introduce Backpropagation Through Time and Space (BPTTS), a method for training a recurrent spatio-temporal neural network, that is used in a homogeneous multi-agent reinforcement learning (MARL) setting to learn numerical methods for hyperbolic conservation laws. We treat the numerical schemes underlying partial differential equations (PDEs) as a Partially Observable Markov Game (POMG) in Reinforcement Learning (RL). Similar to numerical solvers, our agent acts at each discrete location of a computational space for efficient and generalizable learning. To learn higher-order spatial methods by acting on local states, the agent must discern how its actions at a given spatiotemporal location affect the future evolution of the state. The manifestation of this non-stationarity is addressed by BPTTS, which allows for the flow of gradients across both space and time. The learned numerical policies are comparable to the SOTA numerics in two settings, the Burgers' Equation and the Euler Equations, and generalize well to other simulation set-ups.

A Dynamically Controlled Recurrent Neural Network for Modeling Dynamical Systems

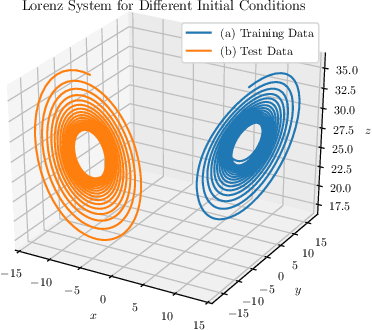
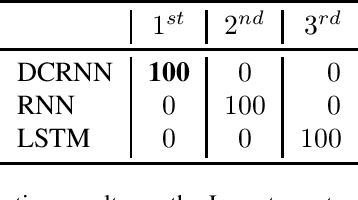
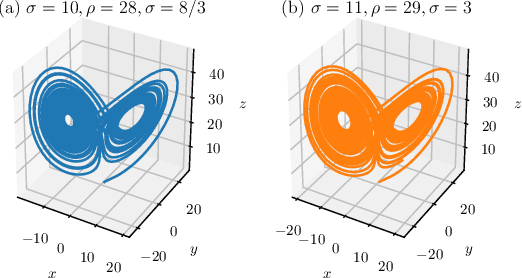
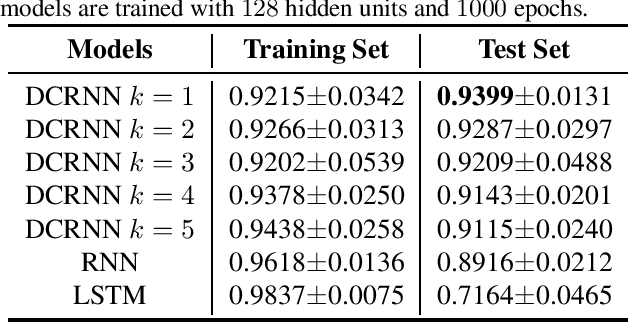
This work proposes a novel neural network architecture, called the Dynamically Controlled Recurrent Neural Network (DCRNN), specifically designed to model dynamical systems that are governed by ordinary differential equations (ODEs). The current state vectors of these types of dynamical systems only depend on their state-space models, along with the respective inputs and initial conditions. Long Short-Term Memory (LSTM) networks, which have proven to be very effective for memory-based tasks, may fail to model physical processes as they tend to memorize, rather than learn how to capture the information on the underlying dynamics. The proposed DCRNN includes learnable skip-connections across previously hidden states, and introduces a regularization term in the loss function by relying on Lyapunov stability theory. The regularizer enables the placement of eigenvalues of the transfer function induced by the DCRNN to desired values, thereby acting as an internal controller for the hidden state trajectory. The results show that, for forecasting a chaotic dynamical system, the DCRNN outperforms the LSTM in $100$ out of $100$ randomized experiments by reducing the mean squared error of the LSTM's forecasting by $80.0\% \pm 3.0\%$.