Multi-Agent Learning of Numerical Methods for Hyperbolic PDEs with Factored Dec-MDP

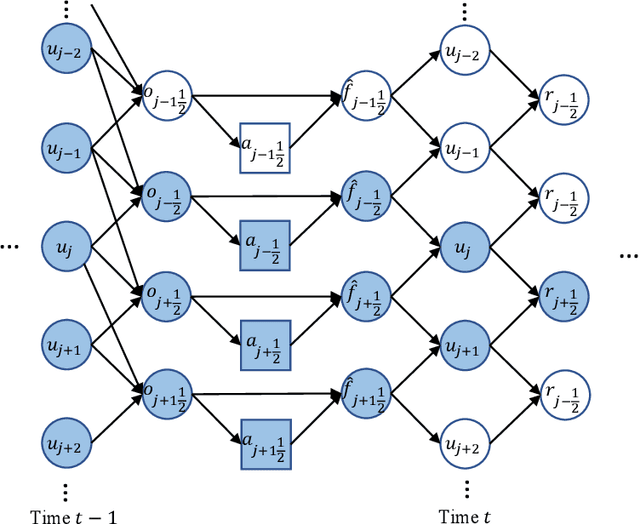
Factored decentralized Markov decision process (Dec-MDP) is a framework for modeling sequential decision making problems in multi-agent systems. In this paper, we formalize the learning of numerical methods for hyperbolic partial differential equations (PDEs), specifically the Weighted Essentially Non-Oscillatory (WENO) scheme, as a factored Dec-MDP problem. We show that different reward formulations lead to either reinforcement learning (RL) or behavior cloning, and a homogeneous policy could be learned for all agents under the RL formulation with a policy gradient algorithm. Because the trained agents only act on their local observations, the multi-agent system can be used as a general numerical method for hyperbolic PDEs and generalize to different spatial discretizations, episode lengths, dimensions, and even equation types.

Backpropagation through Time and Space: Learning Numerical Methods with Multi-Agent Reinforcement Learning

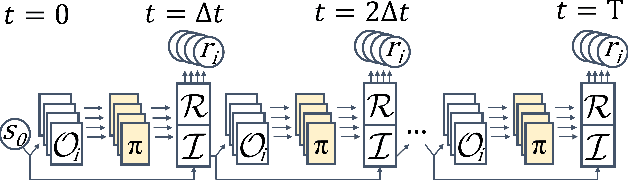
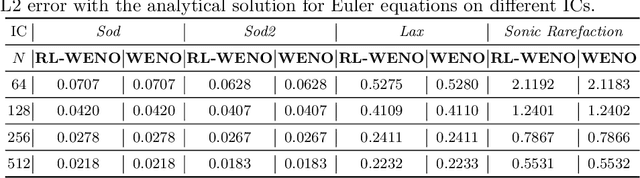
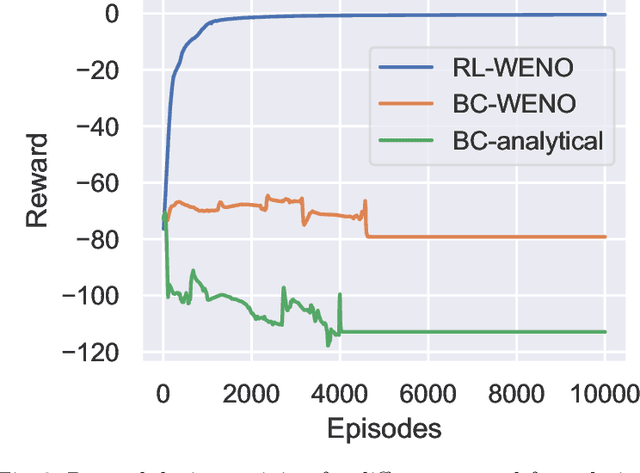
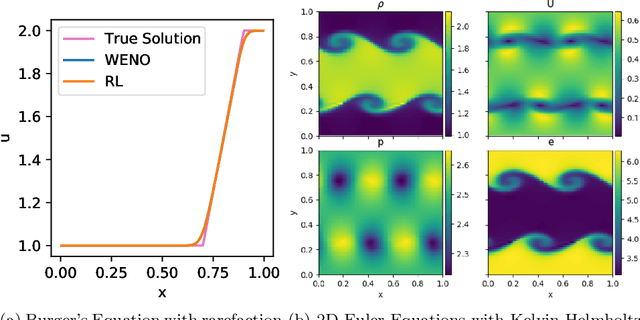
We introduce Backpropagation Through Time and Space (BPTTS), a method for training a recurrent spatio-temporal neural network, that is used in a homogeneous multi-agent reinforcement learning (MARL) setting to learn numerical methods for hyperbolic conservation laws. We treat the numerical schemes underlying partial differential equations (PDEs) as a Partially Observable Markov Game (POMG) in Reinforcement Learning (RL). Similar to numerical solvers, our agent acts at each discrete location of a computational space for efficient and generalizable learning. To learn higher-order spatial methods by acting on local states, the agent must discern how its actions at a given spatiotemporal location affect the future evolution of the state. The manifestation of this non-stationarity is addressed by BPTTS, which allows for the flow of gradients across both space and time. The learned numerical policies are comparable to the SOTA numerics in two settings, the Burgers' Equation and the Euler Equations, and generalize well to other simulation set-ups.