Multi-Agent Learning of Numerical Methods for Hyperbolic PDEs with Factored Dec-MDP
Paper and Code
May 31, 2022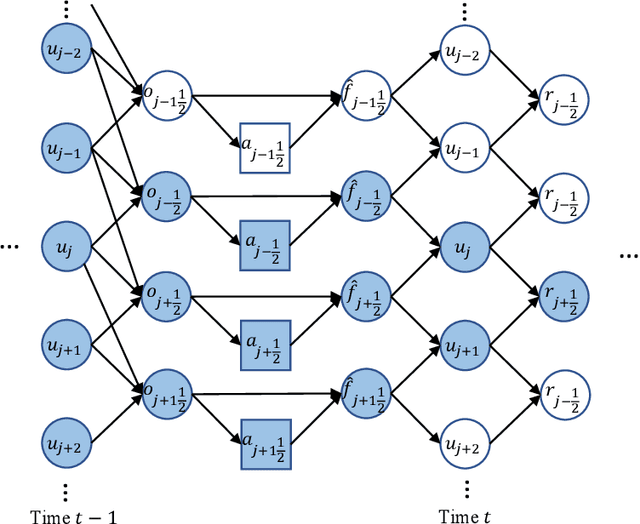
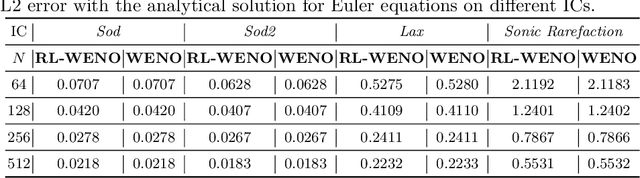
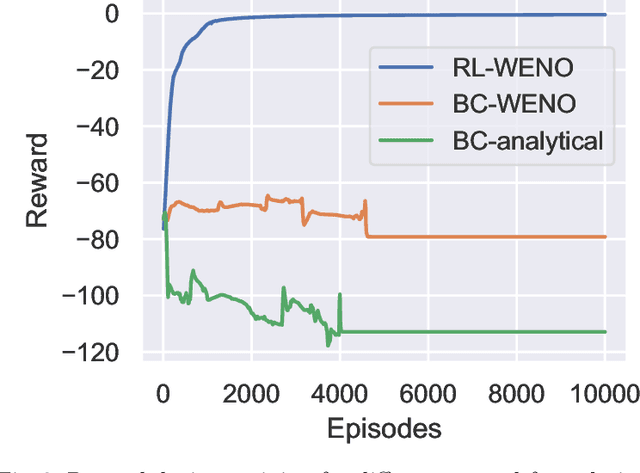
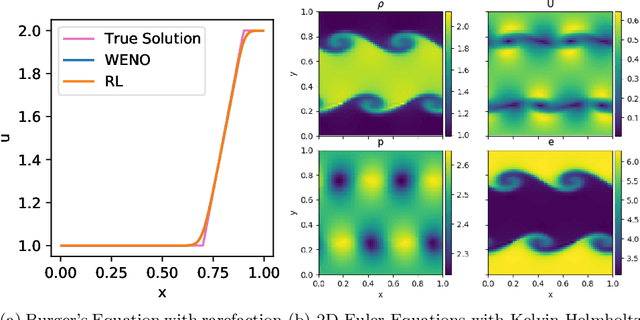
Factored decentralized Markov decision process (Dec-MDP) is a framework for modeling sequential decision making problems in multi-agent systems. In this paper, we formalize the learning of numerical methods for hyperbolic partial differential equations (PDEs), specifically the Weighted Essentially Non-Oscillatory (WENO) scheme, as a factored Dec-MDP problem. We show that different reward formulations lead to either reinforcement learning (RL) or behavior cloning, and a homogeneous policy could be learned for all agents under the RL formulation with a policy gradient algorithm. Because the trained agents only act on their local observations, the multi-agent system can be used as a general numerical method for hyperbolic PDEs and generalize to different spatial discretizations, episode lengths, dimensions, and even equation types.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge