ShapeFit: Exact location recovery from corrupted pairwise directions
Paper and Code
Jul 04, 2015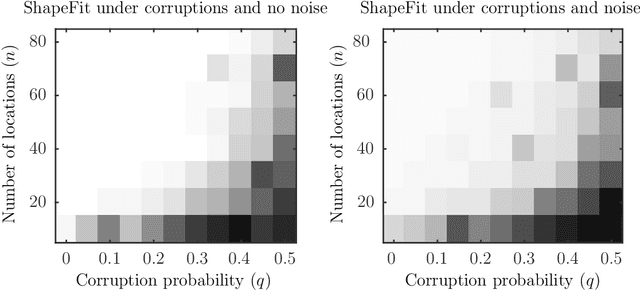
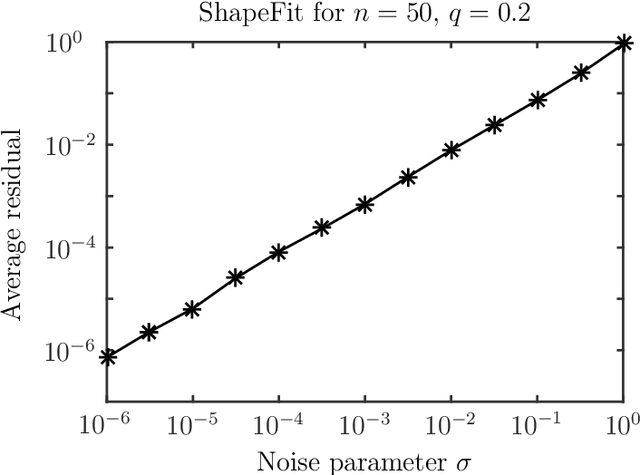
Let $t_1,\ldots,t_n \in \mathbb{R}^d$ and consider the location recovery problem: given a subset of pairwise direction observations $\{(t_i - t_j) / \|t_i - t_j\|_2\}_{i<j \in [n] \times [n]}$, where a constant fraction of these observations are arbitrarily corrupted, find $\{t_i\}_{i=1}^n$ up to a global translation and scale. We propose a novel algorithm for the location recovery problem, which consists of a simple convex program over $dn$ real variables. We prove that this program recovers a set of $n$ i.i.d. Gaussian locations exactly and with high probability if the observations are given by an \erdosrenyi graph, $d$ is large enough, and provided that at most a constant fraction of observations involving any particular location are adversarially corrupted. We also prove that the program exactly recovers Gaussian locations for $d=3$ if the fraction of corrupted observations at each location is, up to poly-logarithmic factors, at most a constant. Both of these recovery theorems are based on a set of deterministic conditions that we prove are sufficient for exact recovery.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge