Onur Ozyesil
A Survey of Structure from Motion
May 09, 2017
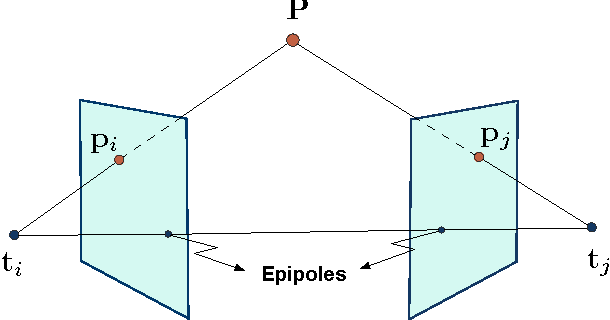

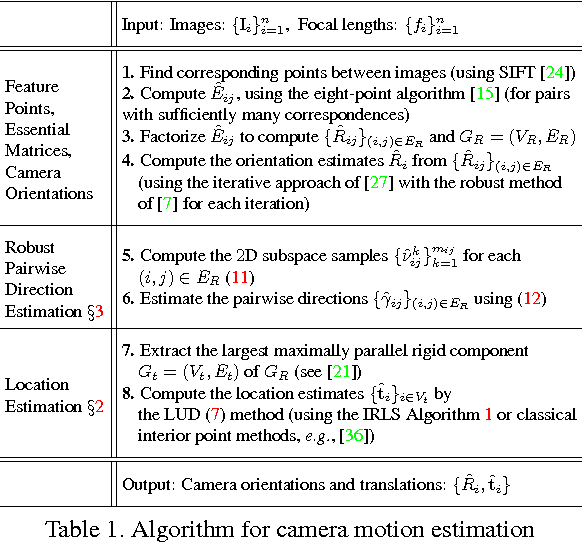
Abstract:The structure from motion (SfM) problem in computer vision is the problem of recovering the three-dimensional ($3$D) structure of a stationary scene from a set of projective measurements, represented as a collection of two-dimensional ($2$D) images, via estimation of motion of the cameras corresponding to these images. In essence, SfM involves the three main stages of (1) extraction of features in images (e.g., points of interest, lines, etc.) and matching these features between images, (2) camera motion estimation (e.g., using relative pairwise camera positions estimated from the extracted features), and (3) recovery of the $3$D structure using the estimated motion and features (e.g., by minimizing the so-called reprojection error). This survey mainly focuses on relatively recent developments in the literature pertaining to stages (2) and (3). More specifically, after touching upon the early factorization-based techniques for motion and structure estimation, we provide a detailed account of some of the recent camera location estimation methods in the literature, followed by discussion of notable techniques for $3$D structure recovery. We also cover the basics of the simultaneous localization and mapping (SLAM) problem, which can be viewed as a specific case of the SfM problem. Further, our survey includes a review of the fundamentals of feature extraction and matching (i.e., stage (1) above), various recent methods for handling ambiguities in $3$D scenes, SfM techniques involving relatively uncommon camera models and image features, and popular sources of data and SfM software.
Robust Camera Location Estimation by Convex Programming
Jun 04, 2015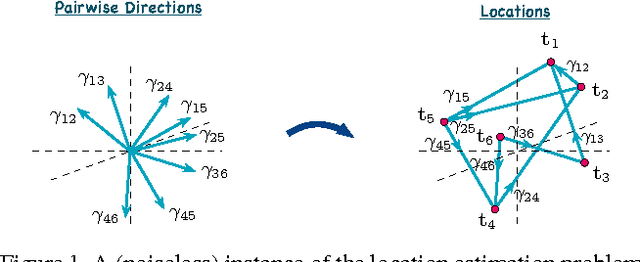
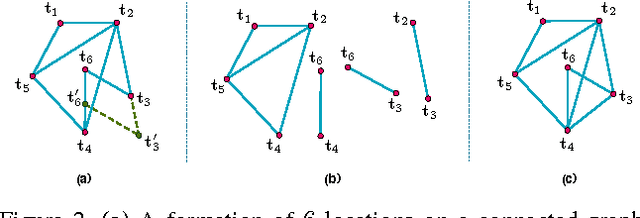
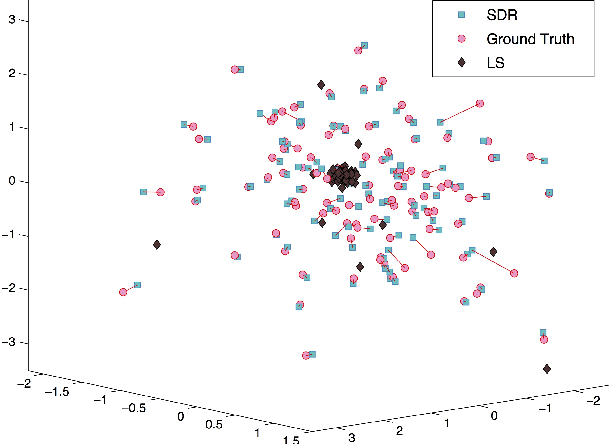
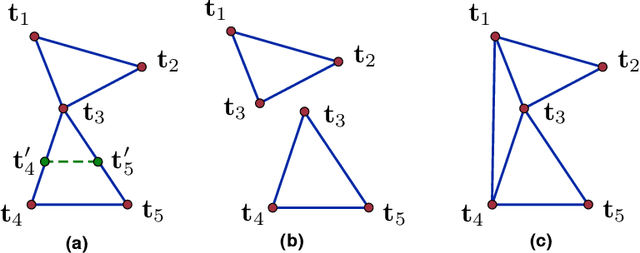
Abstract:$3$D structure recovery from a collection of $2$D images requires the estimation of the camera locations and orientations, i.e. the camera motion. For large, irregular collections of images, existing methods for the location estimation part, which can be formulated as the inverse problem of estimating $n$ locations $\mathbf{t}_1, \mathbf{t}_2, \ldots, \mathbf{t}_n$ in $\mathbb{R}^3$ from noisy measurements of a subset of the pairwise directions $\frac{\mathbf{t}_i - \mathbf{t}_j}{\|\mathbf{t}_i - \mathbf{t}_j\|}$, are sensitive to outliers in direction measurements. In this paper, we firstly provide a complete characterization of well-posed instances of the location estimation problem, by presenting its relation to the existing theory of parallel rigidity. For robust estimation of camera locations, we introduce a two-step approach, comprised of a pairwise direction estimation method robust to outliers in point correspondences between image pairs, and a convex program to maintain robustness to outlier directions. In the presence of partially corrupted measurements, we empirically demonstrate that our convex formulation can even recover the locations exactly. Lastly, we demonstrate the utility of our formulations through experiments on Internet photo collections.
Stable Camera Motion Estimation Using Convex Programming
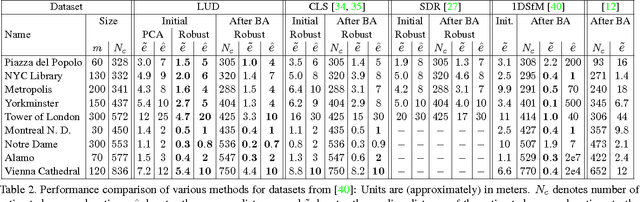
Jan 15, 2015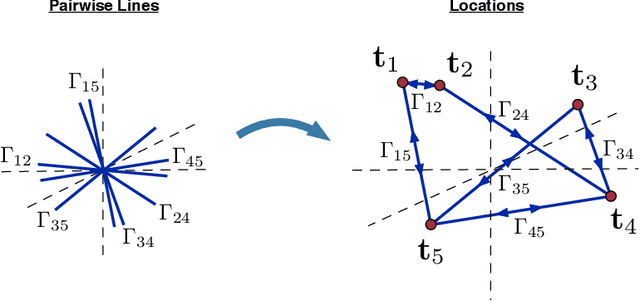

Abstract:We study the inverse problem of estimating n locations $t_1, ..., t_n$ (up to global scale, translation and negation) in $R^d$ from noisy measurements of a subset of the (unsigned) pairwise lines that connect them, that is, from noisy measurements of $\pm (t_i - t_j)/\|t_i - t_j\|$ for some pairs (i,j) (where the signs are unknown). This problem is at the core of the structure from motion (SfM) problem in computer vision, where the $t_i$'s represent camera locations in $R^3$. The noiseless version of the problem, with exact line measurements, has been considered previously under the general title of parallel rigidity theory, mainly in order to characterize the conditions for unique realization of locations. For noisy pairwise line measurements, current methods tend to produce spurious solutions that are clustered around a few locations. This sensitivity of the location estimates is a well-known problem in SfM, especially for large, irregular collections of images. In this paper we introduce a semidefinite programming (SDP) formulation, specially tailored to overcome the clustering phenomenon. We further identify the implications of parallel rigidity theory for the location estimation problem to be well-posed, and prove exact (in the noiseless case) and stable location recovery results. We also formulate an alternating direction method to solve the resulting semidefinite program, and provide a distributed version of our formulation for large numbers of locations. Specifically for the camera location estimation problem, we formulate a pairwise line estimation method based on robust camera orientation and subspace estimation. Lastly, we demonstrate the utility of our algorithm through experiments on real images.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge