Robust Camera Location Estimation by Convex Programming
Paper and Code
Jun 04, 2015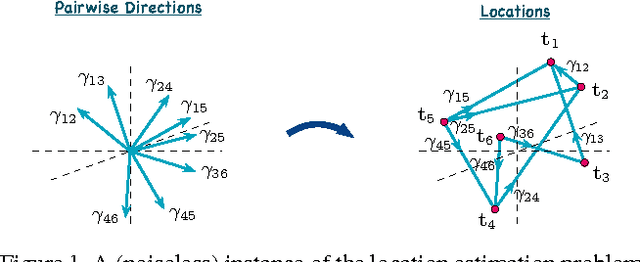
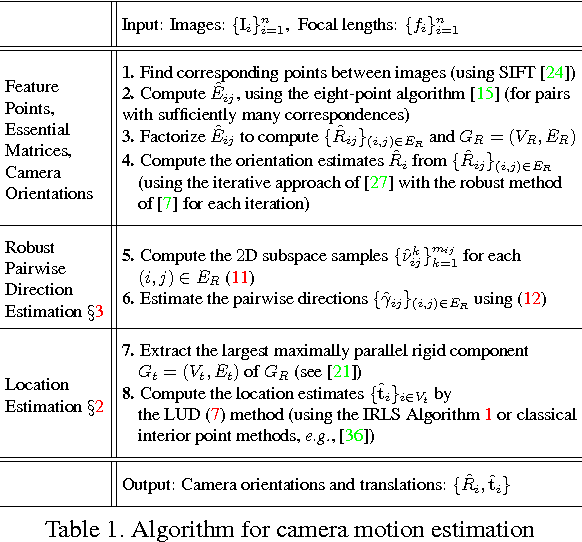
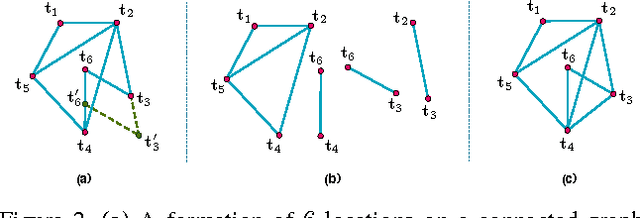
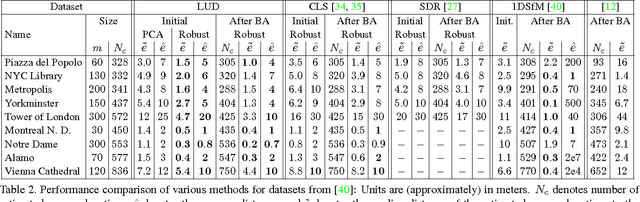
$3$D structure recovery from a collection of $2$D images requires the estimation of the camera locations and orientations, i.e. the camera motion. For large, irregular collections of images, existing methods for the location estimation part, which can be formulated as the inverse problem of estimating $n$ locations $\mathbf{t}_1, \mathbf{t}_2, \ldots, \mathbf{t}_n$ in $\mathbb{R}^3$ from noisy measurements of a subset of the pairwise directions $\frac{\mathbf{t}_i - \mathbf{t}_j}{\|\mathbf{t}_i - \mathbf{t}_j\|}$, are sensitive to outliers in direction measurements. In this paper, we firstly provide a complete characterization of well-posed instances of the location estimation problem, by presenting its relation to the existing theory of parallel rigidity. For robust estimation of camera locations, we introduce a two-step approach, comprised of a pairwise direction estimation method robust to outliers in point correspondences between image pairs, and a convex program to maintain robustness to outlier directions. In the presence of partially corrupted measurements, we empirically demonstrate that our convex formulation can even recover the locations exactly. Lastly, we demonstrate the utility of our formulations through experiments on Internet photo collections.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge