Stable Camera Motion Estimation Using Convex Programming
Paper and Code
Jan 15, 2015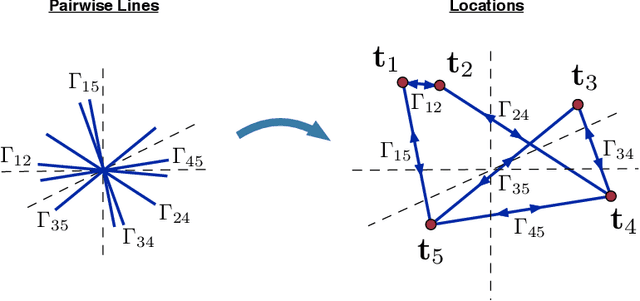

We study the inverse problem of estimating n locations $t_1, ..., t_n$ (up to global scale, translation and negation) in $R^d$ from noisy measurements of a subset of the (unsigned) pairwise lines that connect them, that is, from noisy measurements of $\pm (t_i - t_j)/\|t_i - t_j\|$ for some pairs (i,j) (where the signs are unknown). This problem is at the core of the structure from motion (SfM) problem in computer vision, where the $t_i$'s represent camera locations in $R^3$. The noiseless version of the problem, with exact line measurements, has been considered previously under the general title of parallel rigidity theory, mainly in order to characterize the conditions for unique realization of locations. For noisy pairwise line measurements, current methods tend to produce spurious solutions that are clustered around a few locations. This sensitivity of the location estimates is a well-known problem in SfM, especially for large, irregular collections of images. In this paper we introduce a semidefinite programming (SDP) formulation, specially tailored to overcome the clustering phenomenon. We further identify the implications of parallel rigidity theory for the location estimation problem to be well-posed, and prove exact (in the noiseless case) and stable location recovery results. We also formulate an alternating direction method to solve the resulting semidefinite program, and provide a distributed version of our formulation for large numbers of locations. Specifically for the camera location estimation problem, we formulate a pairwise line estimation method based on robust camera orientation and subspace estimation. Lastly, we demonstrate the utility of our algorithm through experiments on real images.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge