Ali Ayremlou
FlatCam: Thin, Bare-Sensor Cameras using Coded Aperture and Computation
Jan 27, 2016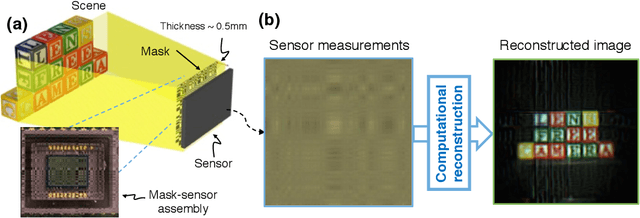
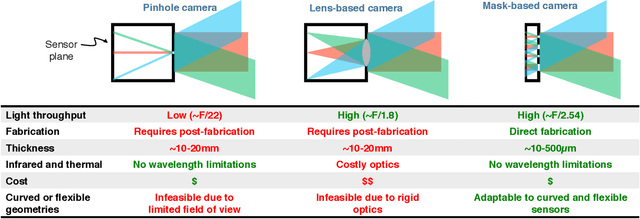
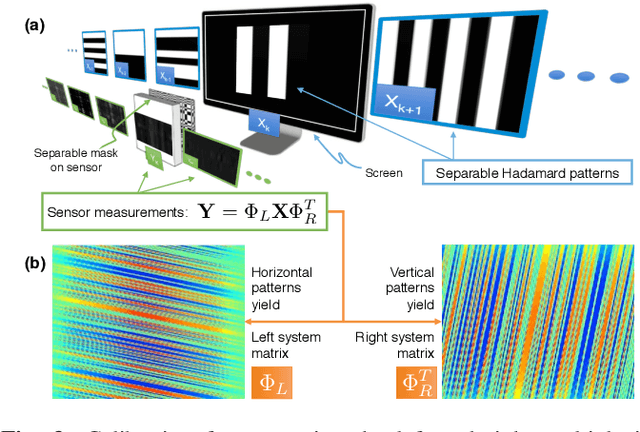

Abstract:FlatCam is a thin form-factor lensless camera that consists of a coded mask placed on top of a bare, conventional sensor array. Unlike a traditional, lens-based camera where an image of the scene is directly recorded on the sensor pixels, each pixel in FlatCam records a linear combination of light from multiple scene elements. A computational algorithm is then used to demultiplex the recorded measurements and reconstruct an image of the scene. FlatCam is an instance of a coded aperture imaging system; however, unlike the vast majority of related work, we place the coded mask extremely close to the image sensor that can enable a thin system. We employ a separable mask to ensure that both calibration and image reconstruction are scalable in terms of memory requirements and computational complexity. We demonstrate the potential of the FlatCam design using two prototypes: one at visible wavelengths and one at infrared wavelengths.
Fast Sublinear Sparse Representation using Shallow Tree Matching Pursuit
Dec 01, 2014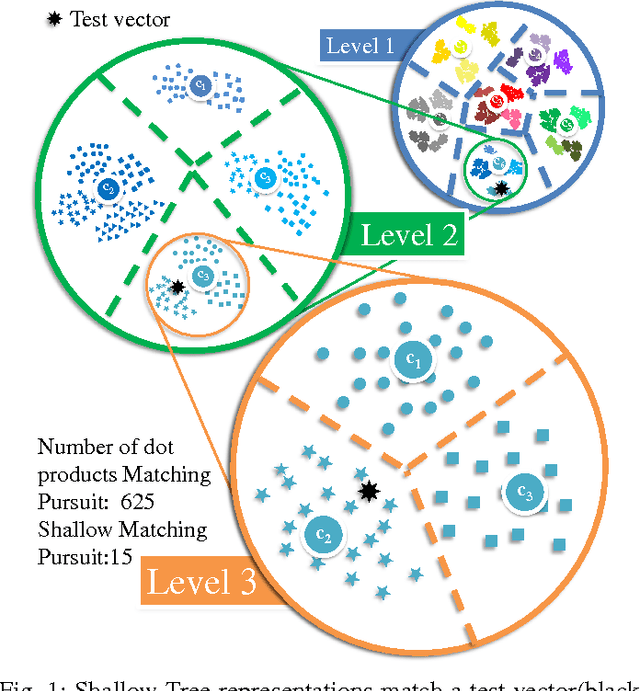
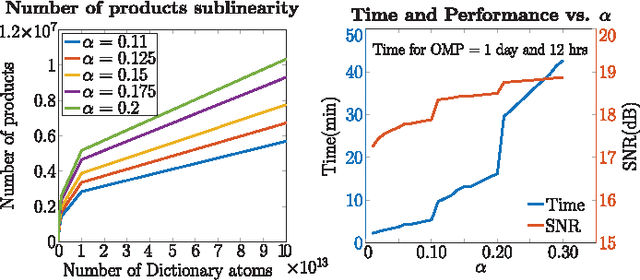


Abstract:Sparse approximations using highly over-complete dictionaries is a state-of-the-art tool for many imaging applications including denoising, super-resolution, compressive sensing, light-field analysis, and object recognition. Unfortunately, the applicability of such methods is severely hampered by the computational burden of sparse approximation: these algorithms are linear or super-linear in both the data dimensionality and size of the dictionary. We propose a framework for learning the hierarchical structure of over-complete dictionaries that enables fast computation of sparse representations. Our method builds on tree-based strategies for nearest neighbor matching, and presents domain-specific enhancements that are highly efficient for the analysis of image patches. Contrary to most popular methods for building spatial data structures, out methods rely on shallow, balanced trees with relatively few layers. We show an extensive array of experiments on several applications such as image denoising/superresolution, compressive video/light-field sensing where we practically achieve 100-1000x speedup (with a less than 1dB loss in accuracy).
Compensating Interpolation Distortion by Using New Optimized Modular Method
Apr 13, 2012
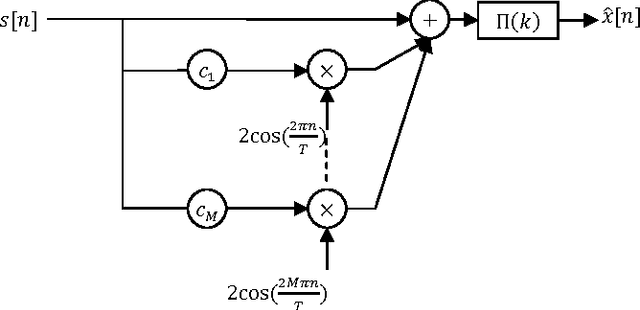
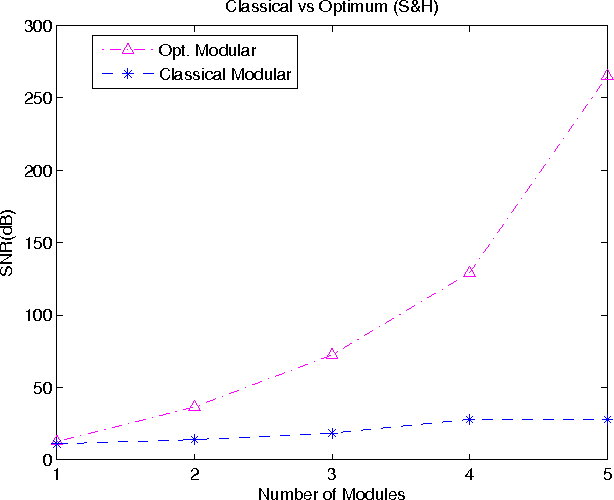

Abstract:A modular method was suggested before to recover a band limited signal from the sample and hold and linearly interpolated (or, in general, an nth-order-hold) version of the regular samples. In this paper a novel approach for compensating the distortion of any interpolation based on modular method has been proposed. In this method the performance of the modular method is optimized by adding only some simply calculated coefficients. This approach causes drastic improvement in terms of signal-to-noise ratios with fewer modules compared to the classical modular method. Simulation results clearly confirm the improvement of the proposed method and also its superior robustness against additive noise.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge