Robust Alignment for Panoramic Stitching via an Exact Rank Constraint

We study the problem of image alignment for panoramic stitching. Unlike most existing approaches that are feature-based, our algorithm works on pixels directly, and accounts for errors across the whole images globally. Technically, we formulate the alignment problem as rank-1 and sparse matrix decomposition over transformed images, and develop an efficient algorithm for solving this challenging non-convex optimization problem. The algorithm reduces to solving a sequence of subproblems, where we analytically establish exact recovery conditions, convergence and optimality, together with convergence rate and complexity. We generalize it to simultaneously align multiple images and recover multiple homographies, extending its application scope towards vast majority of practical scenarios. Experimental results demonstrate that the proposed algorithm is capable of more accurately aligning the images and generating higher quality stitched images than state-of-the-art methods.

An Algorithm Unrolling Approach to Deep Blind Image Deblurring

Blind image deblurring remains a topic of enduring interest. Learning based approaches, especially those that employ neural networks have emerged to complement traditional model based methods and in many cases achieve vastly enhanced performance. That said, neural network approaches are generally empirically designed and the underlying structures are difficult to interpret. In recent years, a promising technique called algorithm unrolling has been developed that has helped connect iterative algorithms such as those for sparse coding to neural network architectures. However, such connections have not been made yet for blind image deblurring. In this paper, we propose a neural network architecture based on this idea. We first present an iterative algorithm that may be considered as a generalization of the traditional total-variation regularization method in the gradient domain. We then unroll the algorithm to construct a neural network for image deblurring which we refer to as Deep Unrolling for Blind Deblurring (DUBLID). Key algorithm parameters are learned with the help of training images. Our proposed deep network DUBLID achieves significant practical performance gains while enjoying interpretability at the same time. Extensive experimental results show that DUBLID outperforms many state-of-the-art methods and in addition is computationally faster.

An Algorithm Unrolling Approach to Deep Image Deblurring

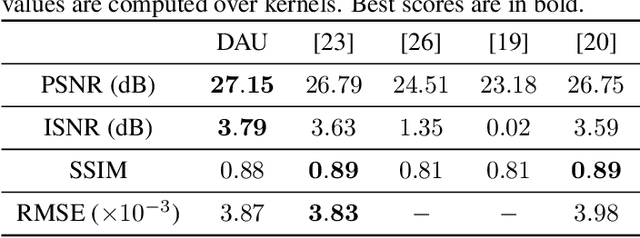
While neural networks have achieved vastly enhanced performance over traditional iterative methods in many cases, they are generally empirically designed and the underlying structures are difficult to interpret. The algorithm unrolling approach has helped connect iterative algorithms to neural network architectures. However, such connections have not been made yet for blind image deblurring. In this paper, we propose a neural network architecture that advances this idea. We first present an iterative algorithm that may be considered a generalization of the traditional total-variation regularization method on the gradient domain, and subsequently unroll the half-quadratic splitting algorithm to construct a neural network. Our proposed deep network achieves significant practical performance gains while enjoying interpretability at the same time. Experimental results show that our approach outperforms many state-of-the-art methods.

Prior Information Guided Regularized Deep Learning for Cell Nucleus Detection

Cell nuclei detection is a challenging research topic because of limitations in cellular image quality and diversity of nuclear morphology, i.e. varying nuclei shapes, sizes, and overlaps between multiple cell nuclei. This has been a topic of enduring interest with promising recent success shown by deep learning methods. These methods train Convolutional Neural Networks (CNNs) with a training set of input images and known, labeled nuclei locations. Many such methods are supplemented by spatial or morphological processing. Using a set of canonical cell nuclei shapes, prepared with the help of a domain expert, we develop a new approach that we call Shape Priors with Convolutional Neural Networks (SP-CNN). We further extend the network to introduce a shape prior (SP) layer and then allowing it to become trainable (i.e. optimizable). We call this network tunable SP-CNN (TSP-CNN). In summary, we present new network structures that can incorporate 'expected behavior' of nucleus shapes via two components: learnable layers that perform the nucleus detection and a fixed processing part that guides the learning with prior information. Analytically, we formulate two new regularization terms that are targeted at: 1) learning the shapes, 2) reducing false positives while simultaneously encouraging detection inside the cell nucleus boundary. Experimental results on two challenging datasets reveal that the proposed SP-CNN and TSP-CNN can outperform state-of-the-art alternatives.

Deep Networks with Shape Priors for Nucleus Detection

Detection of cell nuclei in microscopic images is a challenging research topic, because of limitations in cellular image quality and diversity of nuclear morphology, i.e. varying nuclei shapes, sizes, and overlaps between multiple cell nuclei. This has been a topic of enduring interest with promising recent success shown by deep learning methods. These methods train for example convolutional neural networks (CNNs) with a training set of input images and known, labeled nuclei locations. Many of these methods are supplemented by spatial or morphological processing. We develop a new approach that we call Shape Priors with Convolutional Neural Networks (SP-CNN) to perform significantly enhanced nuclei detection. A set of canonical shapes is prepared with the help of a domain expert. Subsequently, we present a new network structure that can incorporate `expected behavior' of nucleus shapes via two components: {\em learnable} layers that perform the nucleus detection and a {\em fixed} processing part that guides the learning with prior information. Analytically, we formulate a new regularization term that is targeted at penalizing false positives while simultaneously encouraging detection inside cell nucleus boundary. Experimental results on a challenging dataset reveal that SP-CNN is competitive with or outperforms several state-of-the-art methods.

Blind Image Deblurring Using Row-Column Sparse Representations

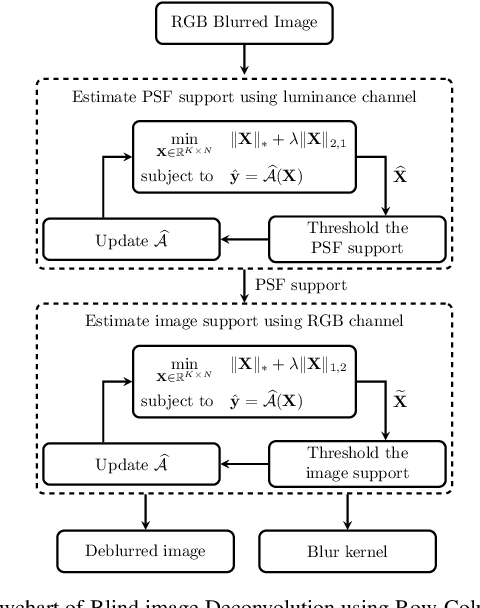
Blind image deblurring is a particularly challenging inverse problem where the blur kernel is unknown and must be estimated en route to recover the deblurred image. The problem is of strong practical relevance since many imaging devices such as cellphone cameras, must rely on deblurring algorithms to yield satisfactory image quality. Despite significant research effort, handling large motions remains an open problem. In this paper, we develop a new method called Blind Image Deblurring using Row-Column Sparsity (BD-RCS) to address this issue. Specifically, we model the outer product of kernel and image coefficients in certain transformation domains as a rank-one matrix, and recover it by solving a rank minimization problem. Our central contribution then includes solving {\em two new} optimization problems involving row and column sparsity to automatically determine blur kernel and image support sequentially. The kernel and image can then be recovered through a singular value decomposition (SVD). Experimental results on linear motion deblurring demonstrate that BD-RCS can yield better results than state of the art, particularly when the blur is caused by large motion. This is confirmed both visually and through quantitative measures.

Phase and TV Based Convex Sets for Blind Deconvolution of Microscopic Images

In this article, two closed and convex sets for blind deconvolution problem are proposed. Most blurring functions in microscopy are symmetric with respect to the origin. Therefore, they do not modify the phase of the Fourier transform (FT) of the original image. As a result blurred image and the original image have the same FT phase. Therefore, the set of images with a prescribed FT phase can be used as a constraint set in blind deconvolution problems. Another convex set that can be used during the image reconstruction process is the epigraph set of Total Variation (TV) function. This set does not need a prescribed upper bound on the total variation of the image. The upper bound is automatically adjusted according to the current image of the restoration process. Both of these two closed and convex sets can be used as a part of any blind deconvolution algorithm. Simulation examples are presented.

Denosing Using Wavelets and Projections onto the L1-Ball

Both wavelet denoising and denosing methods using the concept of sparsity are based on soft-thresholding. In sparsity based denoising methods, it is assumed that the original signal is sparse in some transform domains such as the wavelet domain and the wavelet subsignals of the noisy signal are projected onto L1-balls to reduce noise. In this lecture note, it is shown that the size of the L1-ball or equivalently the soft threshold value can be determined using linear algebra. The key step is an orthogonal projection onto the epigraph set of the L1-norm cost function.

Signal Reconstruction Framework Based On Projections Onto Epigraph Set Of A Convex Cost Function (PESC)

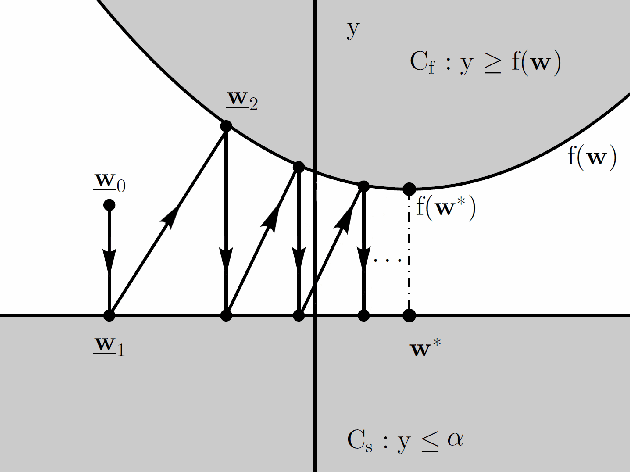
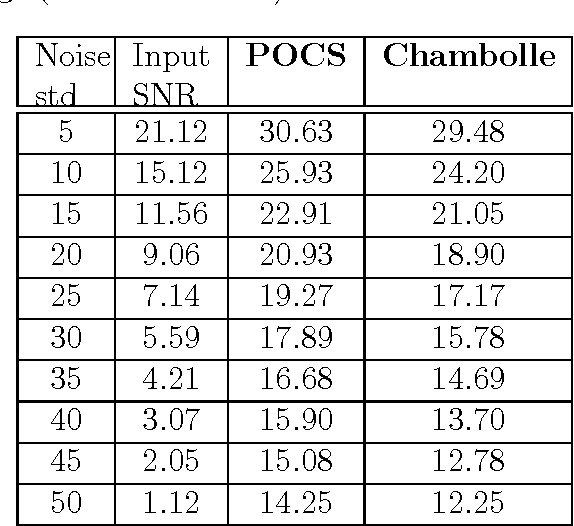
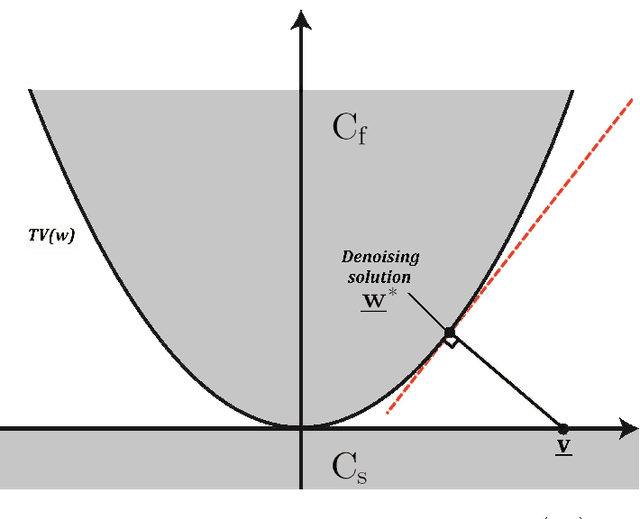
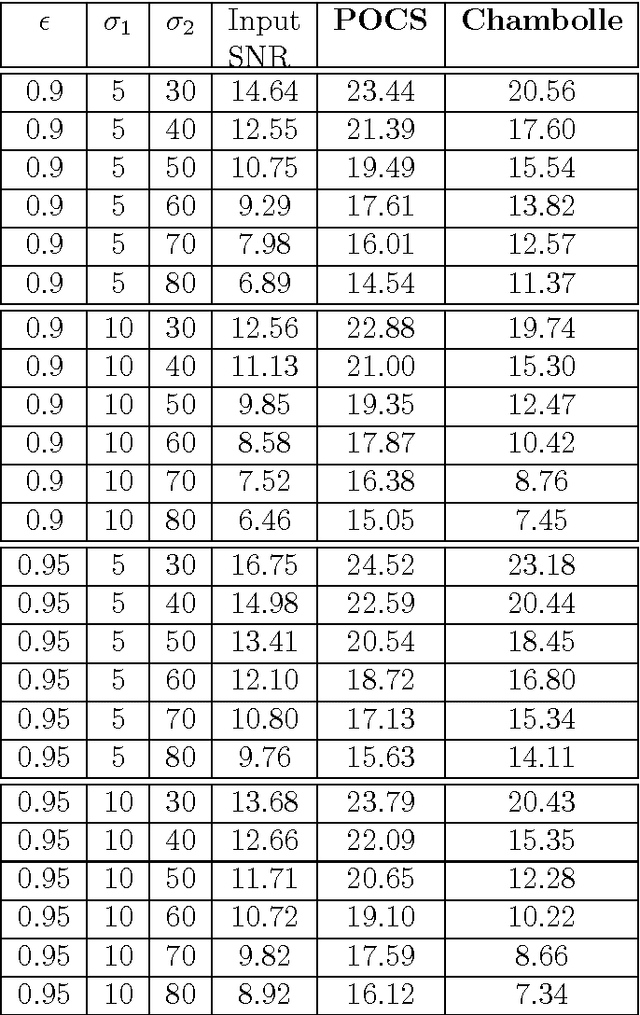
A new signal processing framework based on making orthogonal Projections onto the Epigraph Set of a Convex cost function (PESC) is developed. In this way it is possible to solve convex optimization problems using the well-known Projections onto Convex Set (POCS) approach. In this algorithm, the dimension of the minimization problem is lifted by one and a convex set corresponding to the epigraph of the cost function is defined. If the cost function is a convex function in $R^N$, the corresponding epigraph set is also a convex set in R^{N+1}. The PESC method provides globally optimal solutions for total-variation (TV), filtered variation (FV), L_1, L_2, and entropic cost function based convex optimization problems. In this article, the PESC based denoising and compressive sensing algorithms are developed. Simulation examples are presented.

Robust Head Pose Estimation Using Contourlet Transform

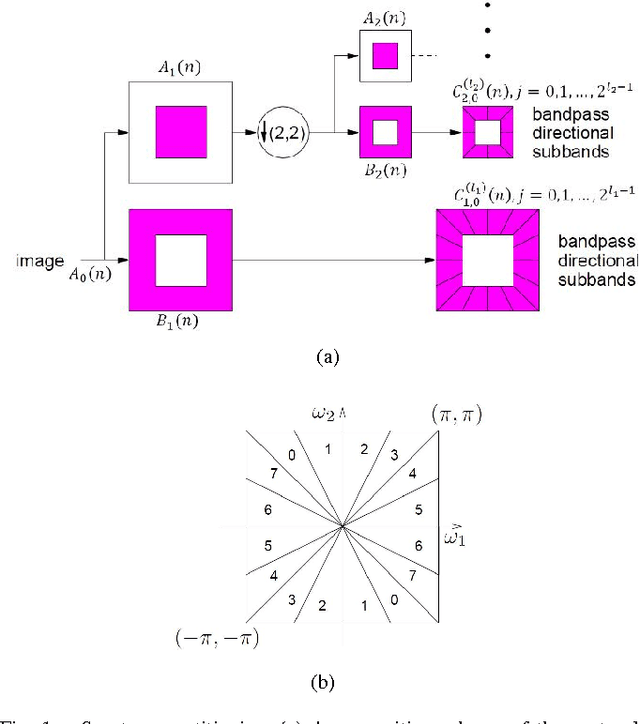
Estimating pose of the head is an important preprocessing step in many pattern recognition and computer vision systems such as face recognition. Since the performance of the face recognition systems is greatly affected by the poses of the face, how to estimate the accurate pose of the face in human face image is still a challenging problem. In this paper, we represent a novel method for head pose estimation. To enhance the efficiency of the estimation we use contourlet transform for feature extraction. Contourlet transform is multi-resolution, multi-direction transform. In order to reduce the feature space dimension and obtain appropriate features we use LDA (Linear Discriminant Analysis) and PCA (Principal Component Analysis) to remove ineffcient features. Then, we apply different classifiers such as k-nearest neighborhood (knn) and minimum distance. We use the public available FERET database to evaluate the performance of proposed method. Simulation results indicate the superior robustness of the proposed method.