Signal Reconstruction Framework Based On Projections Onto Epigraph Set Of A Convex Cost Function (PESC)

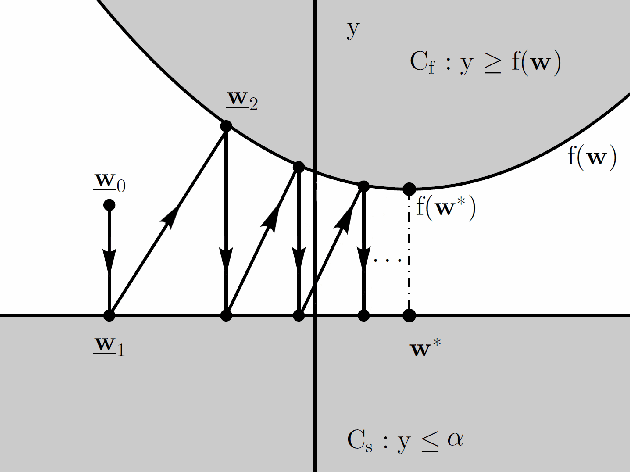
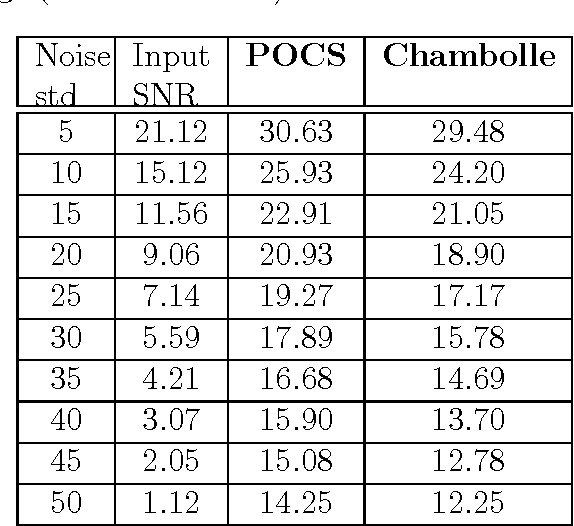
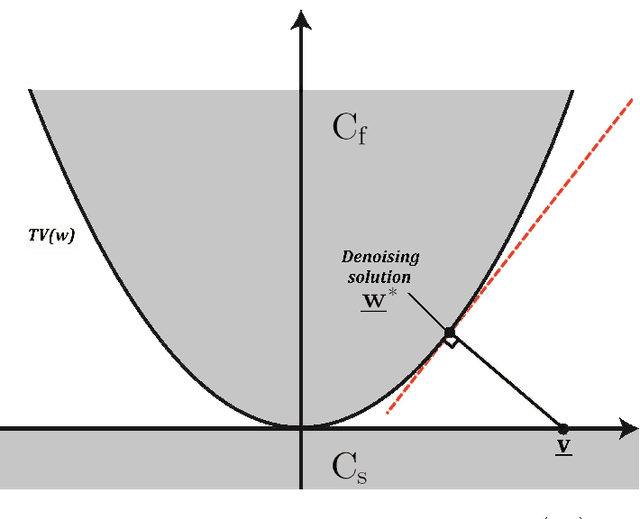
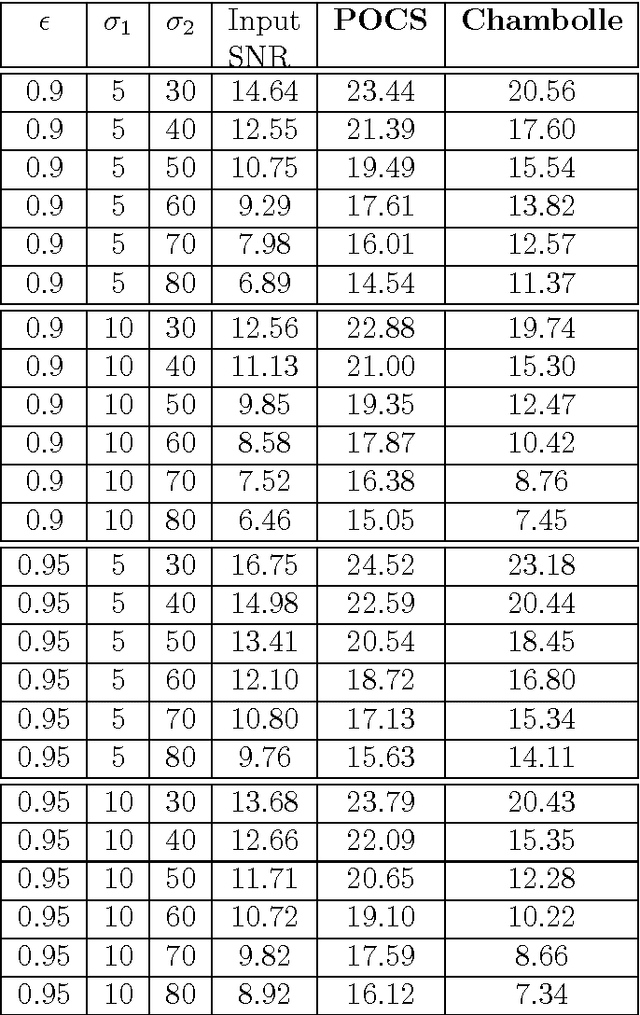
A new signal processing framework based on making orthogonal Projections onto the Epigraph Set of a Convex cost function (PESC) is developed. In this way it is possible to solve convex optimization problems using the well-known Projections onto Convex Set (POCS) approach. In this algorithm, the dimension of the minimization problem is lifted by one and a convex set corresponding to the epigraph of the cost function is defined. If the cost function is a convex function in $R^N$, the corresponding epigraph set is also a convex set in R^{N+1}. The PESC method provides globally optimal solutions for total-variation (TV), filtered variation (FV), L_1, L_2, and entropic cost function based convex optimization problems. In this article, the PESC based denoising and compressive sensing algorithms are developed. Simulation examples are presented.