Robust Alignment for Panoramic Stitching via an Exact Rank Constraint
Paper and Code
Apr 01, 2019
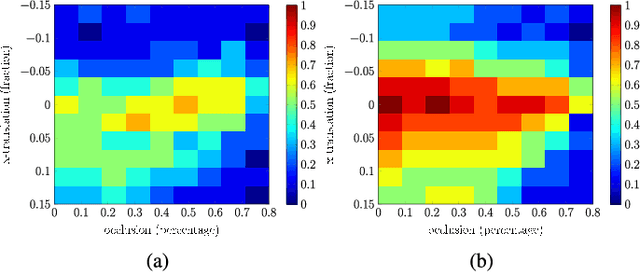


We study the problem of image alignment for panoramic stitching. Unlike most existing approaches that are feature-based, our algorithm works on pixels directly, and accounts for errors across the whole images globally. Technically, we formulate the alignment problem as rank-1 and sparse matrix decomposition over transformed images, and develop an efficient algorithm for solving this challenging non-convex optimization problem. The algorithm reduces to solving a sequence of subproblems, where we analytically establish exact recovery conditions, convergence and optimality, together with convergence rate and complexity. We generalize it to simultaneously align multiple images and recover multiple homographies, extending its application scope towards vast majority of practical scenarios. Experimental results demonstrate that the proposed algorithm is capable of more accurately aligning the images and generating higher quality stitched images than state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge