Equivariant IMU Preintegration with Biases: a Galilean Group Approach

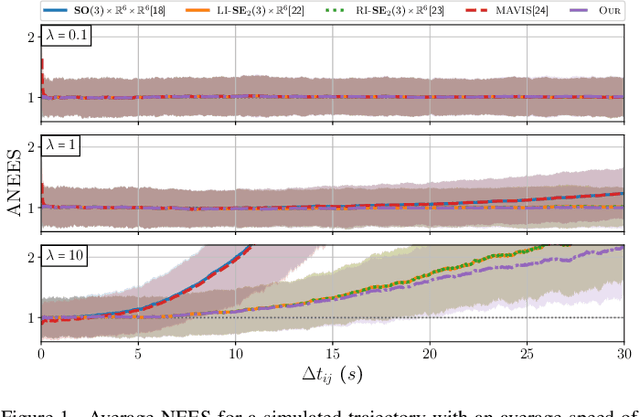
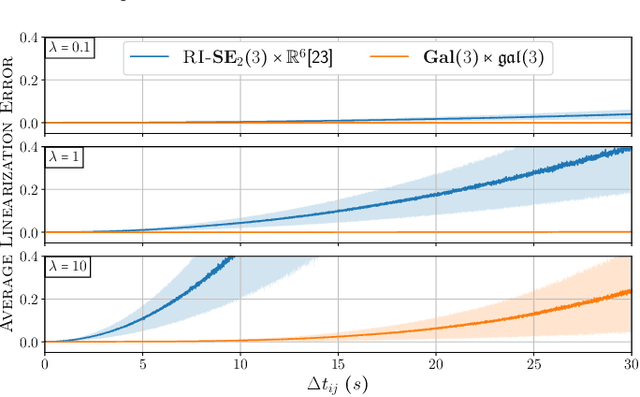
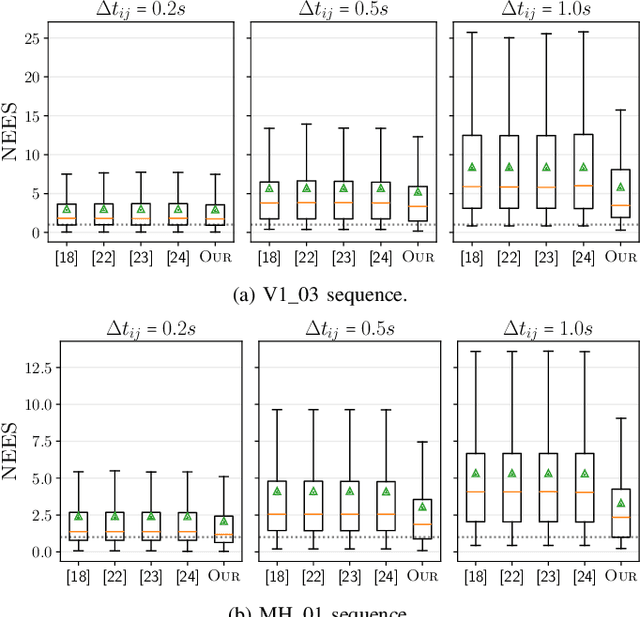
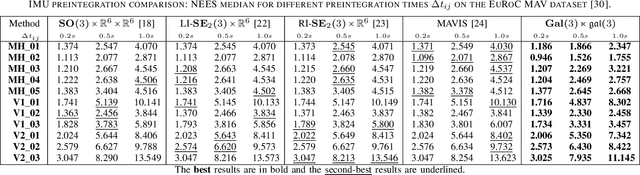
This letter proposes a new approach for Inertial Measurement Unit (IMU) preintegration, a fundamental building block that can be leveraged in different optimization-based Inertial Navigation System (INS) localization solutions. Inspired by recent advances in equivariant theory applied to biased INSs, we derive a discrete-time formulation of the IMU preintegration on ${\mathbf{Gal}(3) \ltimes \mathfrak{gal}(3)}$, the left-trivialization of the tangent group of the Galilean group $\mathbf{Gal}(3)$. We define a novel preintegration error that geometrically couples the navigation states and the bias leading to lower linearization error. Our method improves in consistency compared to existing preintegration approaches which treat IMU biases as a separate state-space. Extensive validation against state-of-the-art methods, both in simulation and with real-world IMU data, implementation in the Lie++ library, and open-source code are provided.

Equivariant IMU Preintegration with Biases: an Inhomogeneous Galilean Group Approach

This letter proposes a new approach for Inertial Measurement Unit (IMU) preintegration, a fundamental building block that can be leveraged in different optimization-based Inertial Navigation System (INS) localization solutions. Inspired by recent advancements in equivariant theory applied to biased INSs, we derive a discrete-time formulation of the IMU preintegration on $\mathbf{G}(3) \ltimes \mathfrak{g}(3)$, the tangent group of the inhomogeneous Galilean group $\mathbf{G}(3)$. We define a novel preintegration error that geometrically couples the navigation states and the bias leading to lower linearization error. Our method improves in consistency compared to existing preintegration approaches which treat IMU biases as a separate state-space. Extensive validation against state-of-the-art methods, both in simulation and with real-world IMU data, implementation in the Lie++ library, and open-sourcing of the code are provided.

AIVIO: Closed-loop, Object-relative Navigation of UAVs with AI-aided Visual Inertial Odometry

Object-relative mobile robot navigation is essential for a variety of tasks, e.g. autonomous critical infrastructure inspection, but requires the capability to extract semantic information about the objects of interest from raw sensory data. While deep learning-based (DL) methods excel at inferring semantic object information from images, such as class and relative 6 degree of freedom (6-DoF) pose, they are computationally demanding and thus often not suitable for payload constrained mobile robots. In this letter we present a real-time capable unmanned aerial vehicle (UAV) system for object-relative, closed-loop navigation with a minimal sensor configuration consisting of an inertial measurement unit (IMU) and RGB camera. Utilizing a DL-based object pose estimator, solely trained on synthetic data and optimized for companion board deployment, the object-relative pose measurements are fused with the IMU data to perform object-relative localization. We conduct multiple real-world experiments to validate the performance of our system for the challenging use case of power pole inspection. An example closed-loop flight is presented in the supplementary video.

Impact of Estimation Errors of a Matrix of Transfer Functions onto Its Analytic Singular Values and Their Potential Algorithmic Extraction

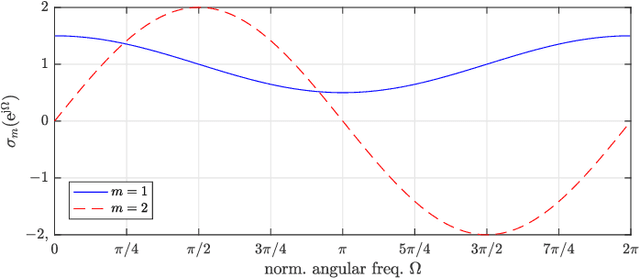
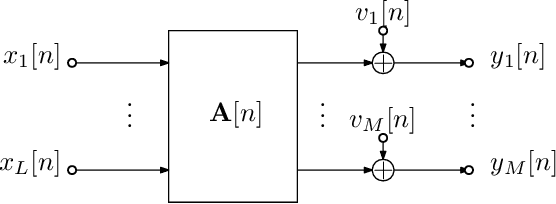
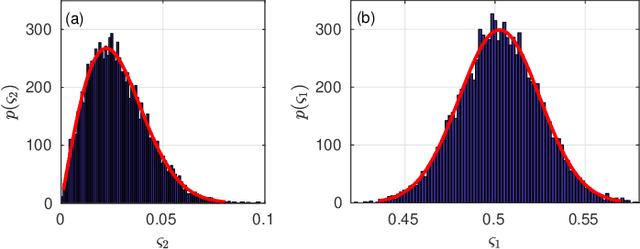
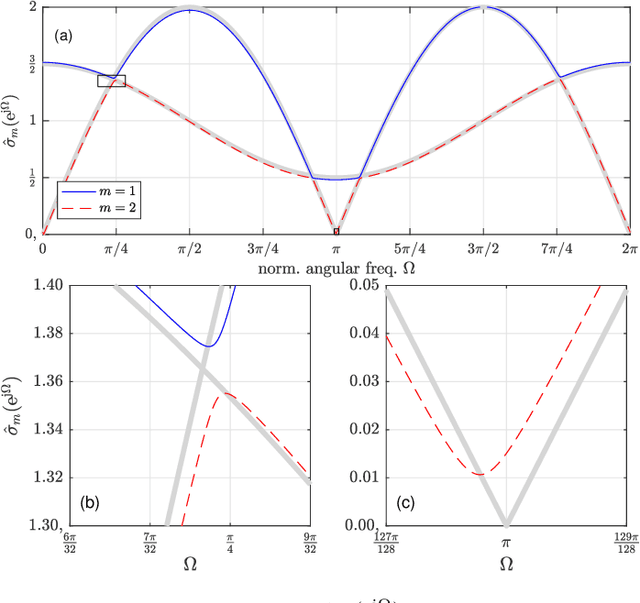
A matrix of analytic functions A(z), such as the matrix of transfer functions in a multiple-input multiple-output (MIMO) system, generally admits an analytic singular value decomposition (SVD), where the singular values themselves are functions. When evaluated on the unit circle, for the sake of analyticity, these singular values must be permitted of become negative. In this paper, we address how the estimation of such a matrix, causing a stochastic perturbation of A}(z), results in fundamental changes to the analytic singular values: for the perturbed system, we show that their analytic singular values lose any algebraic multiplicities and are strictly non-negative with probability one. We present examples and highlight the impact that this has on algorithmic solutions to extracting an analytic or approximate analytic SVD.

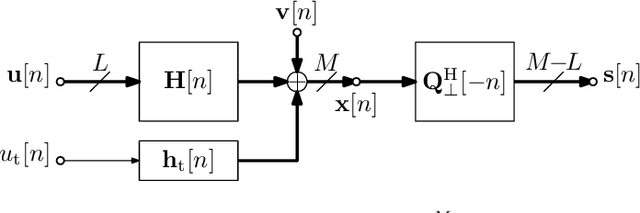
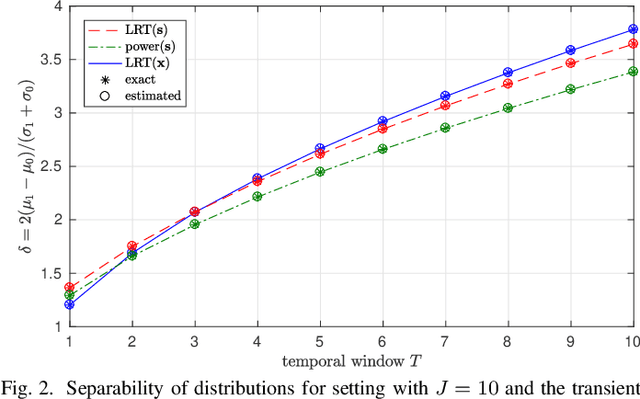
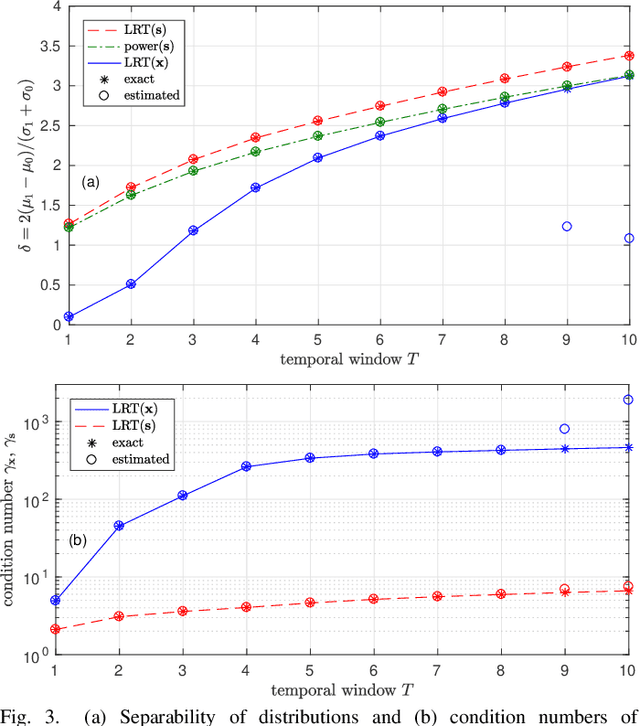
Computational and Numerical Properties of a Broadband Subspace-Based Likelihood Ratio Test

This paper investigates the performance of a likelihood ratio test in combination with a polynomial subspace projection approach to detect weak transient signals in broadband array data. Based on previous empirical evidence that a likelihood ratio test is advantageously applied in a lower-dimensional subspace, we present analysis that highlights how the polynomial subspace projection whitens a crucial part of the signals, enabling a detector to operate with a shortened temporal window. This reduction in temporal correlation, together with a spatial compaction of the data, also leads to both computational and numerical advantages over a likelihood ratio test that is directly applied to the array data. The results of our analysis are illustrated by examples and simulations.

Modular Meshed Ultra-Wideband Aided Inertial Navigation with Robust Anchor Calibration

This paper introduces a generic filter-based state estimation framework that supports two state-decoupling strategies based on cross-covariance factorization. These strategies reduce the computational complexity and inherently support true modularity -- a perquisite for handling and processing meshed range measurements among a time-varying set of devices. In order to utilize these measurements in the estimation framework, positions of newly detected stationary devices (anchors) and the pairwise biases between the ranging devices are required. In this work an autonomous calibration procedure for new anchors is presented, that utilizes range measurements from multiple tags as well as already known anchors. To improve the robustness, an outlier rejection method is introduced. After the calibration is performed, the sensor fusion framework obtains initial beliefs of the anchor positions and dictionaries of pairwise biases, in order to fuse range measurements obtained from new anchors tightly-coupled. The effectiveness of the filter and calibration framework has been validated through evaluations on a recorded dataset and real-world experiments.

Siamese Residual Neural Network for Musical Shape Evaluation in Piano Performance Assessment

Understanding and identifying musical shape plays an important role in music education and performance assessment. To simplify the otherwise time- and cost-intensive musical shape evaluation, in this paper we explore how artificial intelligence (AI) driven models can be applied. Considering musical shape evaluation as a classification problem, a light-weight Siamese residual neural network (S-ResNN) is proposed to automatically identify musical shapes. To assess the proposed approach in the context of piano musical shape evaluation, we have generated a new dataset, containing 4116 music pieces derived by 147 piano preparatory exercises and performed in 28 categories of musical shapes. The experimental results show that the S-ResNN significantly outperforms a number of benchmark methods in terms of the precision, recall and F1 score.

MSCEqF: A Multi State Constraint Equivariant Filter for Vision-aided Inertial Navigation

This letter re-visits the problem of visual-inertial navigation system (VINS) and presents a novel filter design we dub the multi state constraint equivariant filter (MSCEqF, in analogy to the well known MSCKF). We define a symmetry group and corresponding group action that allow specifically the design of an equivariant filter for the problem of visual-inertial odometry (VIO) including IMU bias, and camera intrinsic and extrinsic calibration states. In contrast to state-of-the-art invariant extended Kalman filter (IEKF) approaches that simply tack IMU bias and other states onto the $\mathbf{SE}_2(3)$ group, our filter builds upon a symmetry that properly includes all the states in the group structure. Thus, we achieve improved behavior, particularly when linearization points largely deviate from the truth (i.e., on transients upon state disturbances). Our approach is inherently consistent even during convergence phases from significant errors without the need for error uncertainty adaptation, observability constraint, or other consistency enforcing techniques. This leads to greatly improved estimator behavior for significant error and unexpected state changes during, e.g., long-duration missions. We evaluate our approach with a multitude of different experiments using three different prominent real-world datasets.

Revisiting multi-GNSS Navigation for UAVs -- An Equivariant Filtering Approach

In this work, we explore the recent advances in equivariant filtering for inertial navigation systems to improve state estimation for uncrewed aerial vehicles (UAVs). Traditional state-of-the-art estimation methods, e.g., the multiplicative Kalman filter (MEKF), have some limitations concerning their consistency, errors in the initial state estimate, and convergence performance. Symmetry-based methods, such as the equivariant filter (EqF), offer significant advantages for these points by exploiting the mathematical properties of the system - its symmetry. These filters yield faster convergence rates and robustness to wrong initial state estimates through their error definition. To demonstrate the usability of EqFs, we focus on the sensor-fusion problem with the most common sensors in outdoor robotics: global navigation satellite system (GNSS) sensors and an inertial measurement unit (IMU). We provide an implementation of such an EqF leveraging the semi-direct product of the symmetry group to derive the filter equations. To validate the practical usability of EqFs in real-world scenarios, we evaluate our method using data from all outdoor runs of the INSANE Dataset. Our results demonstrate the performance improvements of the EqF in real-world environments, highlighting its potential for enhancing state estimation for UAVs.

Equivariant Symmetries for Inertial Navigation Systems

This paper investigates the problem of inertial navigation system (INS) filter design through the lens of symmetry. The extended Kalman filter (EKF) and its variants, have been the staple of INS filtering for 50 years; however, recent advances in inertial navigation systems have exploited matrix Lie group structure to design stochastic filters and state observers that have been shown to display superior performance compared to classical solutions. In this work we consider the case where a vehicle has an inertial measurement unit (IMU) and a global navigation satellite system (GNSS) receiver. We show that all the modern variants of the EKF for these sensors can be interpreted as the recently proposed Equivariant Filter (EqF) design methodology applied to different choices of symmetry group for the INS problem. This leads us to propose two new symmetries for the INS problem that have not been considered in the prior literature, and provide a discussion of the relative strengths and weaknesses of all the different algorithms. We believe the collection of symmetries that we present here capture all the sensible choices of symmetry for this problem and sensor suite, and that the analysis provided is indicative of the relative real-world performance potential of the different algorithms.