Impact of Estimation Errors of a Matrix of Transfer Functions onto Its Analytic Singular Values and Their Potential Algorithmic Extraction

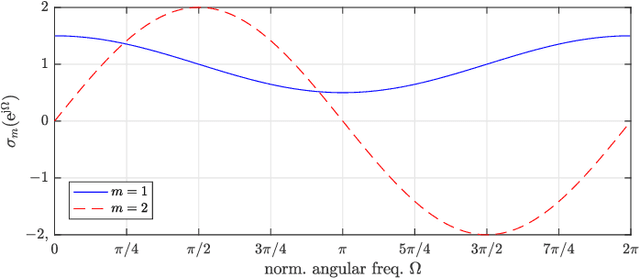
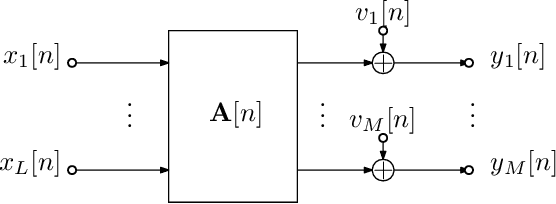
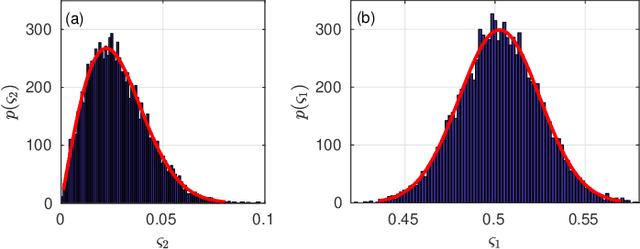
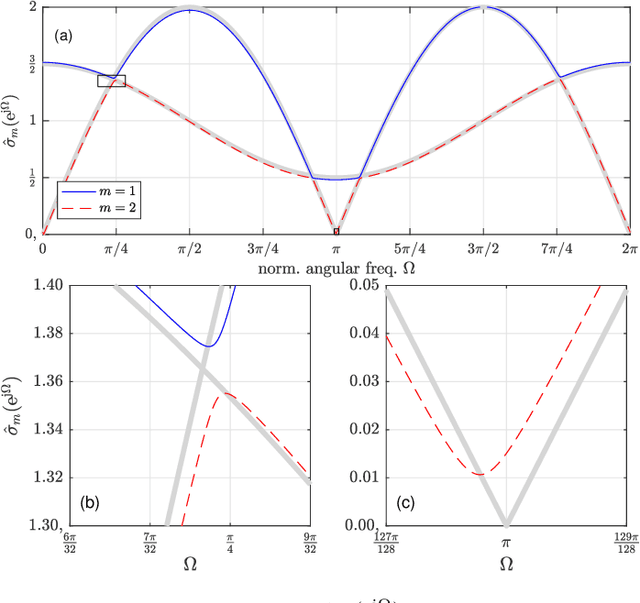
A matrix of analytic functions A(z), such as the matrix of transfer functions in a multiple-input multiple-output (MIMO) system, generally admits an analytic singular value decomposition (SVD), where the singular values themselves are functions. When evaluated on the unit circle, for the sake of analyticity, these singular values must be permitted of become negative. In this paper, we address how the estimation of such a matrix, causing a stochastic perturbation of A}(z), results in fundamental changes to the analytic singular values: for the perturbed system, we show that their analytic singular values lose any algebraic multiplicities and are strictly non-negative with probability one. We present examples and highlight the impact that this has on algorithmic solutions to extracting an analytic or approximate analytic SVD.

A Gaussian Process Regression based Dynamical Models Learning Algorithm for Target Tracking

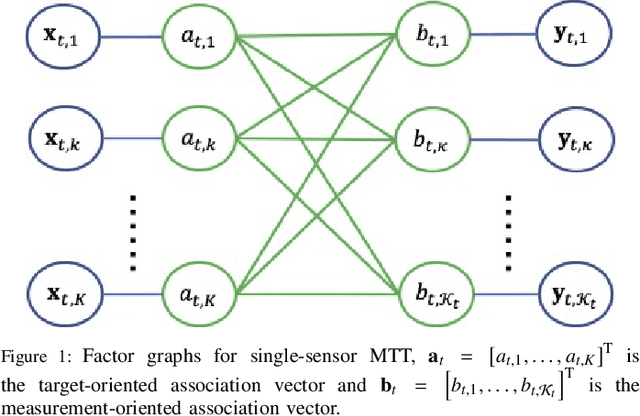
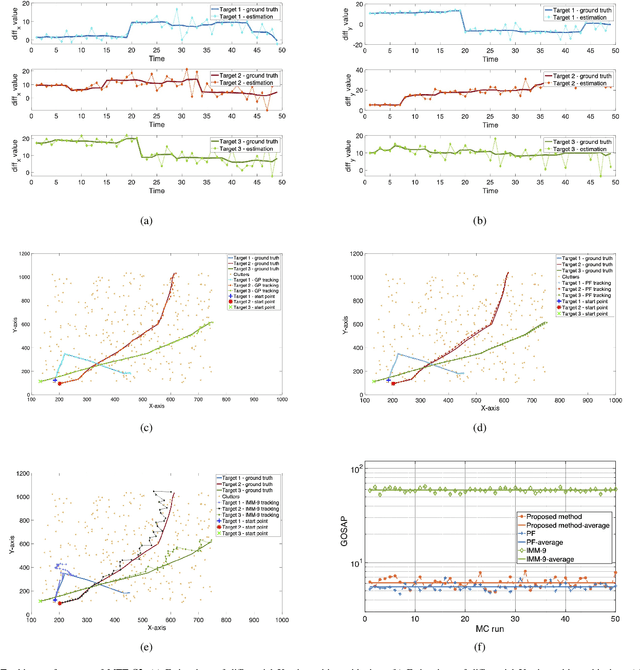
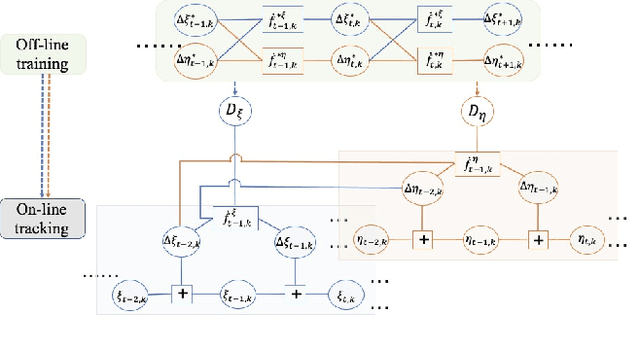
Maneuvering target tracking is a challenging problem for sensor systems because of the unpredictability of the targets' motions. This paper proposes a novel data-driven method for learning the dynamical motion model of a target. Non-parametric Gaussian process regression (GPR) is used to learn a target's naturally shift invariant motion (NSIM) behavior, which is translationally invariant and does not need to be constantly updated as the target moves. The learned Gaussian processes (GPs) can be applied to track targets within different surveillance regions from the surveillance region of the training data by being incorporated into the particle filter (PF) implementation. The performance of our proposed approach is evaluated over different maneuvering scenarios by being compared with commonly used interacting multiple model (IMM)-PF methods and provides around $90\%$ performance improvement for a multi-target tracking (MTT) highly maneuvering scenario.

Adaptive Kernel Kalman Filter

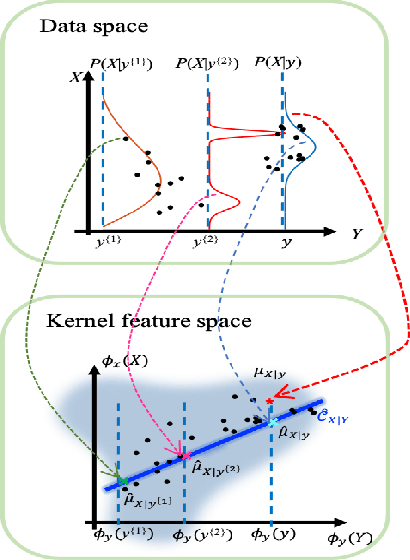
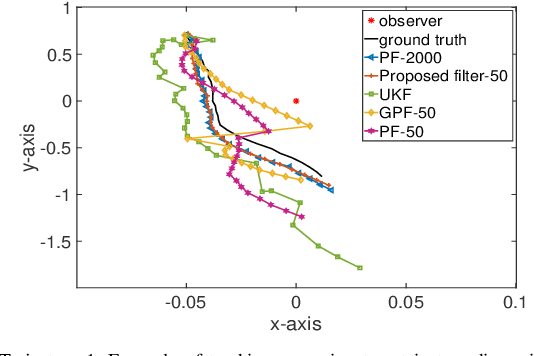
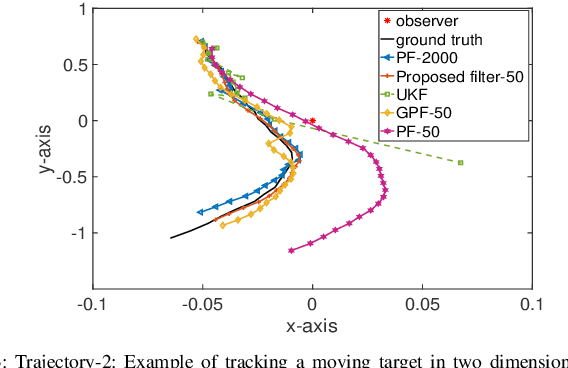
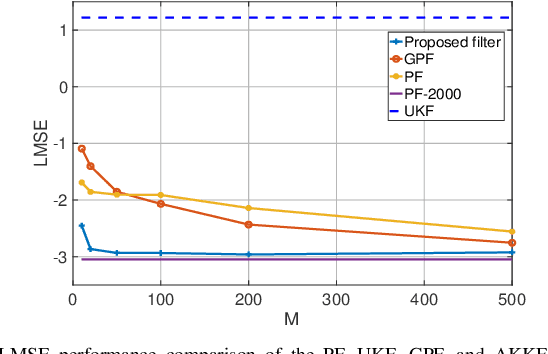
Sequential Bayesian filters in non-linear dynamic systems require the recursive estimation of the predictive and posterior distributions. This paper introduces a Bayesian filter called the adaptive kernel Kalman filter (AKKF). With this filter, the arbitrary predictive and posterior distributions of hidden states are approximated using the empirical kernel mean embeddings (KMEs) in reproducing kernel Hilbert spaces (RKHSs). In parallel with the KMEs, some particles, in the data space, are used to capture the properties of the dynamical system model. Specifically, particles are generated and updated in the data space, while the corresponding kernel weight mean vector and covariance matrix associated with the feature mappings of the particles are predicted and updated in the RKHSs based on the kernel Kalman rule (KKR). Simulation results are presented to confirm the improved performance of our approach with significantly reduced particle numbers, by comparing with the unscented Kalman filter (UKF), particle filter (PF) and Gaussian particle filter (GPF). For example, compared with the GPF, the proposed approach provides around 5% logarithmic mean square error (LMSE) tracking performance improvement in the bearing-only tracking (BOT) system when using 50 particles.