Data-Driven Approaches for Modelling Target Behaviour

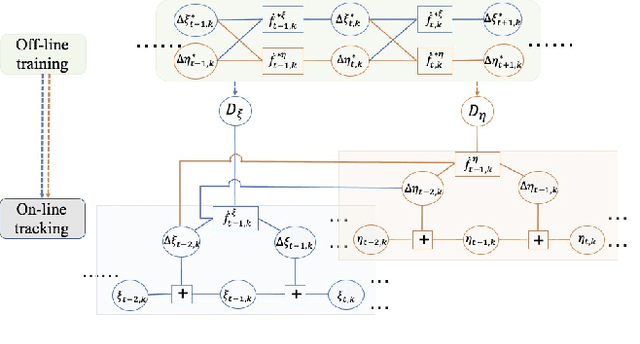
The performance of tracking algorithms strongly depends on the chosen model assumptions regarding the target dynamics. If there is a strong mismatch between the chosen model and the true object motion, the track quality may be poor or the track is easily lost. Still, the true dynamics might not be known a priori or it is too complex to be expressed in a tractable mathematical formulation. This paper provides a comparative study between three different methods that use machine learning to describe the underlying object motion based on training data. The first method builds on Gaussian Processes (GPs) for predicting the object motion, the second learns the parameters of an Interacting Multiple Model (IMM) filter and the third uses a Long Short-Term Memory (LSTM) network as a motion model. All methods are compared against an Extended Kalman Filter (EKF) with an analytic motion model as a benchmark and their respective strengths are highlighted in one simulated and two real-world scenarios.

A Gaussian Process Regression based Dynamical Models Learning Algorithm for Target Tracking

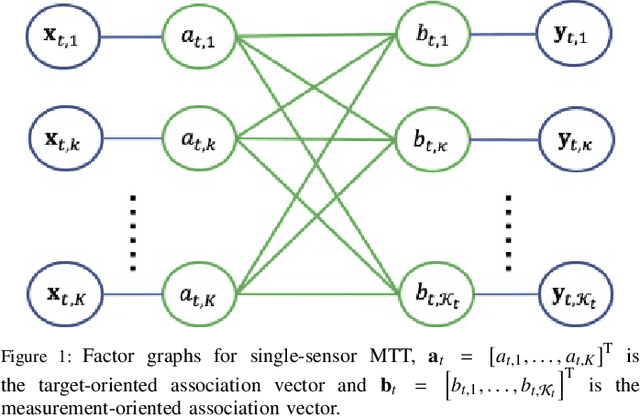
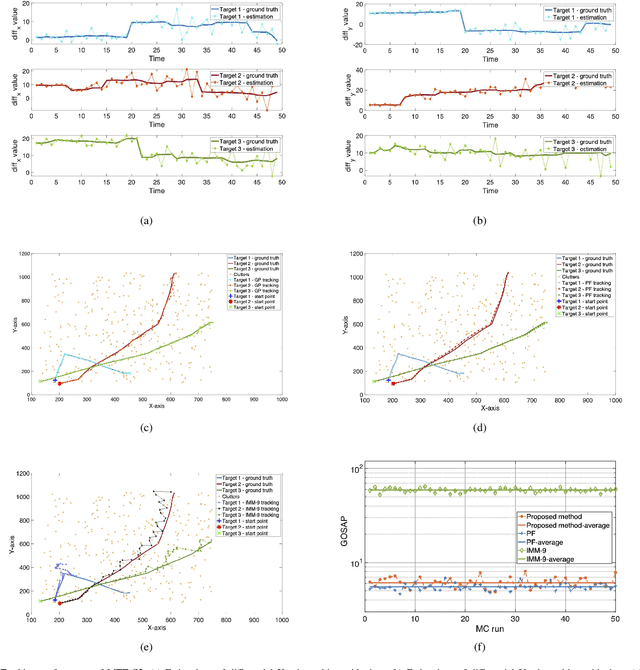
Maneuvering target tracking is a challenging problem for sensor systems because of the unpredictability of the targets' motions. This paper proposes a novel data-driven method for learning the dynamical motion model of a target. Non-parametric Gaussian process regression (GPR) is used to learn a target's naturally shift invariant motion (NSIM) behavior, which is translationally invariant and does not need to be constantly updated as the target moves. The learned Gaussian processes (GPs) can be applied to track targets within different surveillance regions from the surveillance region of the training data by being incorporated into the particle filter (PF) implementation. The performance of our proposed approach is evaluated over different maneuvering scenarios by being compared with commonly used interacting multiple model (IMM)-PF methods and provides around $90\%$ performance improvement for a multi-target tracking (MTT) highly maneuvering scenario.

Adaptive Kernel Kalman Filter

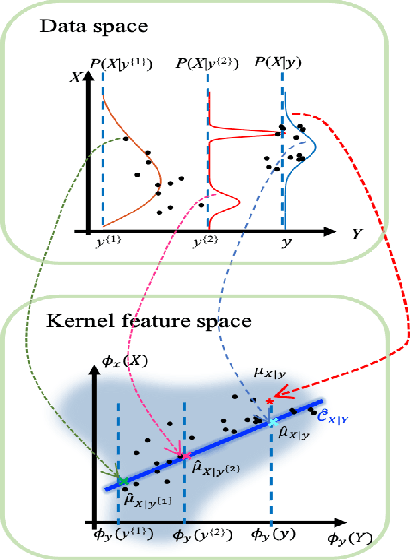
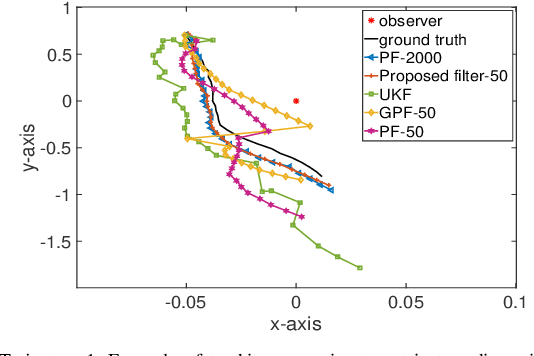
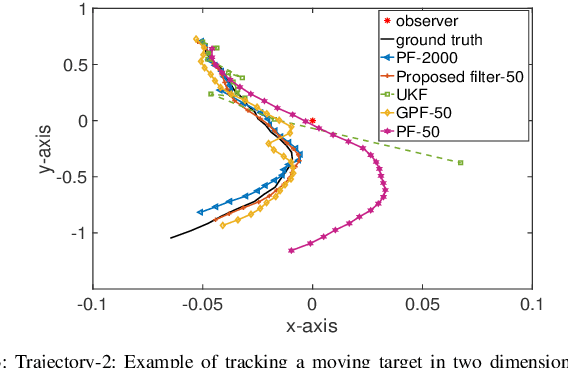
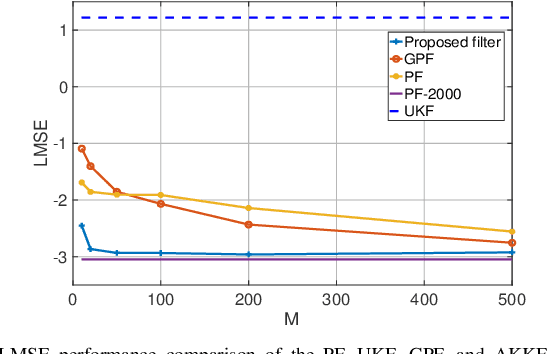
Sequential Bayesian filters in non-linear dynamic systems require the recursive estimation of the predictive and posterior distributions. This paper introduces a Bayesian filter called the adaptive kernel Kalman filter (AKKF). With this filter, the arbitrary predictive and posterior distributions of hidden states are approximated using the empirical kernel mean embeddings (KMEs) in reproducing kernel Hilbert spaces (RKHSs). In parallel with the KMEs, some particles, in the data space, are used to capture the properties of the dynamical system model. Specifically, particles are generated and updated in the data space, while the corresponding kernel weight mean vector and covariance matrix associated with the feature mappings of the particles are predicted and updated in the RKHSs based on the kernel Kalman rule (KKR). Simulation results are presented to confirm the improved performance of our approach with significantly reduced particle numbers, by comparing with the unscented Kalman filter (UKF), particle filter (PF) and Gaussian particle filter (GPF). For example, compared with the GPF, the proposed approach provides around 5% logarithmic mean square error (LMSE) tracking performance improvement in the bearing-only tracking (BOT) system when using 50 particles.