Adaptive Kernel Kalman Filter
Paper and Code
Mar 15, 2022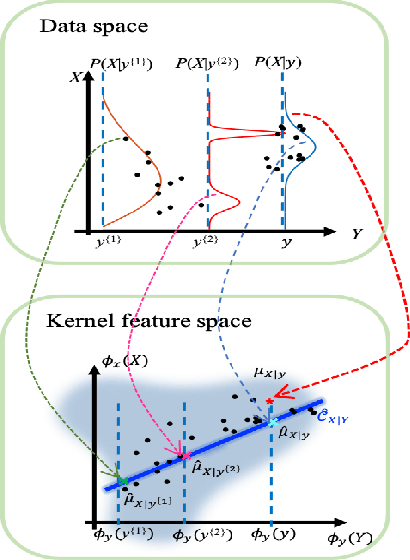
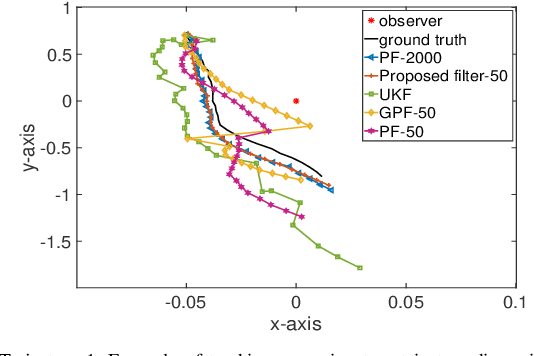
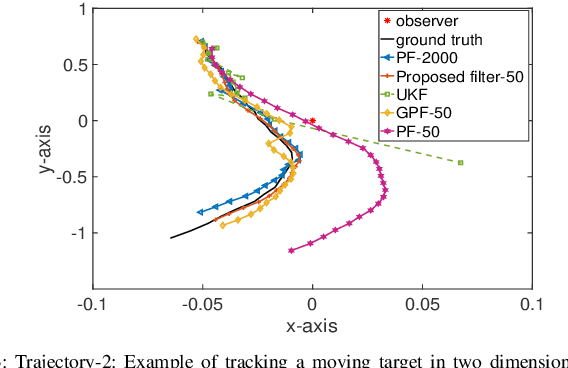
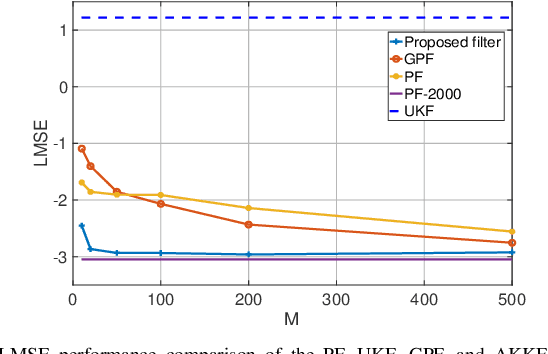
Sequential Bayesian filters in non-linear dynamic systems require the recursive estimation of the predictive and posterior distributions. This paper introduces a Bayesian filter called the adaptive kernel Kalman filter (AKKF). With this filter, the arbitrary predictive and posterior distributions of hidden states are approximated using the empirical kernel mean embeddings (KMEs) in reproducing kernel Hilbert spaces (RKHSs). In parallel with the KMEs, some particles, in the data space, are used to capture the properties of the dynamical system model. Specifically, particles are generated and updated in the data space, while the corresponding kernel weight mean vector and covariance matrix associated with the feature mappings of the particles are predicted and updated in the RKHSs based on the kernel Kalman rule (KKR). Simulation results are presented to confirm the improved performance of our approach with significantly reduced particle numbers, by comparing with the unscented Kalman filter (UKF), particle filter (PF) and Gaussian particle filter (GPF). For example, compared with the GPF, the proposed approach provides around 5% logarithmic mean square error (LMSE) tracking performance improvement in the bearing-only tracking (BOT) system when using 50 particles.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge