Least-Squares Khatri-Rao Factorization of a Polynomial Matrix

The Khatri-Rao product is extensively used in array processing, tensor decomposition, and multi-way data analysis. Many applications require a least-squares (LS) Khatri-Rao factorization. In broadband sensor array problems, polynomial matrices effectively model frequency-dependent behaviors, necessitating extensions of conventional linear algebra techniques. This paper generalizes LS Khatri-Rao factorization from ordinary to polynomial matrices by applying it to the discrete Fourier transform (DFT) samples of polynomial matrices. Phase coherence across bin-wise Khatri-Rao factors is ensured via a phasesmoothing algorithm. The proposed method is validated through broadband angle-of-arrival (AoA) estimation for uniform planar arrays (UPAs), where the steering matrix is a polynomial matrix, which can be represented as a Khatri-Rao product between steering matrix in azimuth and elevation directions.

Impact of Estimation Errors of a Matrix of Transfer Functions onto Its Analytic Singular Values and Their Potential Algorithmic Extraction

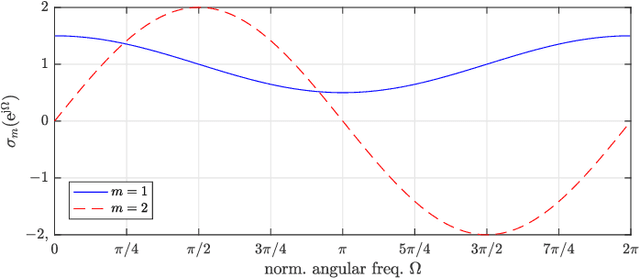
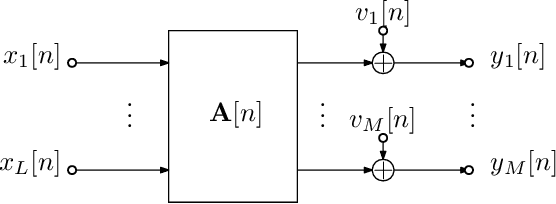
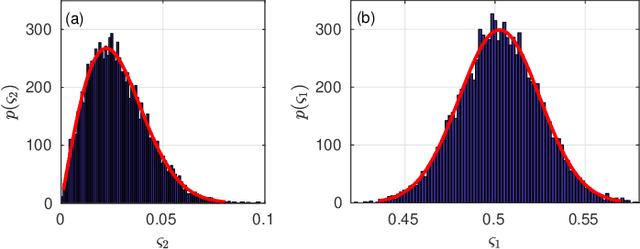
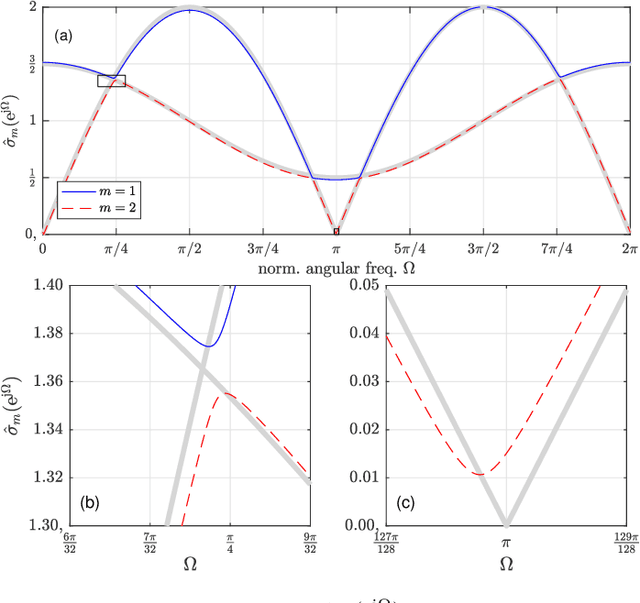
A matrix of analytic functions A(z), such as the matrix of transfer functions in a multiple-input multiple-output (MIMO) system, generally admits an analytic singular value decomposition (SVD), where the singular values themselves are functions. When evaluated on the unit circle, for the sake of analyticity, these singular values must be permitted of become negative. In this paper, we address how the estimation of such a matrix, causing a stochastic perturbation of A}(z), results in fundamental changes to the analytic singular values: for the perturbed system, we show that their analytic singular values lose any algebraic multiplicities and are strictly non-negative with probability one. We present examples and highlight the impact that this has on algorithmic solutions to extracting an analytic or approximate analytic SVD.