Real-Time Initialization of Unknown Anchors for UWB-aided Navigation

This paper presents a framework for the real-time initialization of unknown Ultra-Wideband (UWB) anchors in UWB-aided navigation systems. The method is designed for localization solutions where UWB modules act as supplementary sensors. Our approach enables the automatic detection and calibration of previously unknown anchors during operation, removing the need for manual setup. By combining an online Positional Dilution of Precision (PDOP) estimation, a lightweight outlier detection method, and an adaptive robust kernel for non-linear optimization, our approach significantly improves robustness and suitability for real-world applications compared to state-of-the-art. In particular, we show that our metric which triggers an initialization decision is more conservative than current ones commonly based on initial linear or non-linear initialization guesses. This allows for better initialization geometry and subsequently lower initialization errors. We demonstrate the proposed approach on two different mobile robots: an autonomous forklift and a quadcopter equipped with a UWB-aided Visual-Inertial Odometry (VIO) framework. The results highlight the effectiveness of the proposed method with robust initialization and low positioning error. We open-source our code in a C++ library including a ROS wrapper.

Equivariant IMU Preintegration with Biases: a Galilean Group Approach

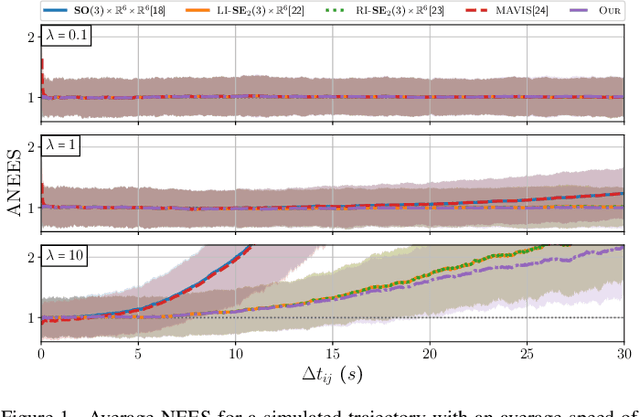
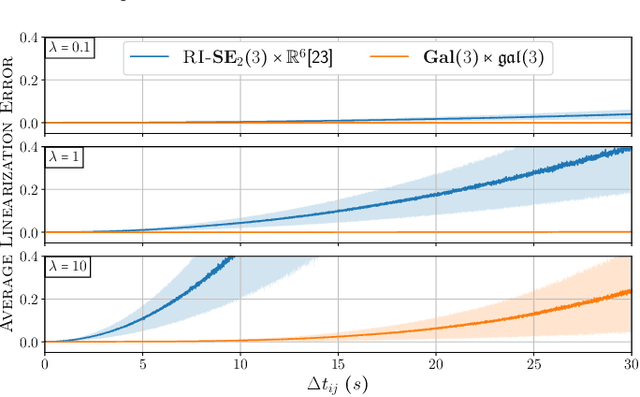
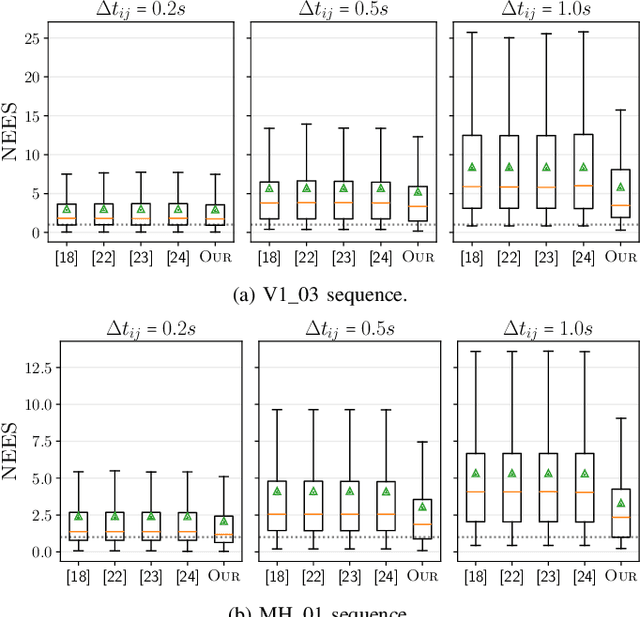
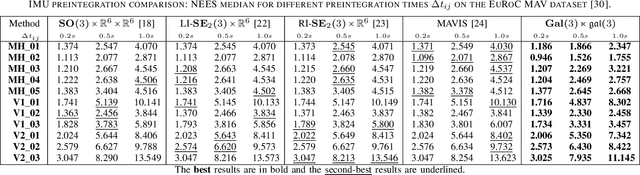
This letter proposes a new approach for Inertial Measurement Unit (IMU) preintegration, a fundamental building block that can be leveraged in different optimization-based Inertial Navigation System (INS) localization solutions. Inspired by recent advances in equivariant theory applied to biased INSs, we derive a discrete-time formulation of the IMU preintegration on ${\mathbf{Gal}(3) \ltimes \mathfrak{gal}(3)}$, the left-trivialization of the tangent group of the Galilean group $\mathbf{Gal}(3)$. We define a novel preintegration error that geometrically couples the navigation states and the bias leading to lower linearization error. Our method improves in consistency compared to existing preintegration approaches which treat IMU biases as a separate state-space. Extensive validation against state-of-the-art methods, both in simulation and with real-world IMU data, implementation in the Lie++ library, and open-source code are provided.

Equivariant IMU Preintegration with Biases: an Inhomogeneous Galilean Group Approach

This letter proposes a new approach for Inertial Measurement Unit (IMU) preintegration, a fundamental building block that can be leveraged in different optimization-based Inertial Navigation System (INS) localization solutions. Inspired by recent advancements in equivariant theory applied to biased INSs, we derive a discrete-time formulation of the IMU preintegration on $\mathbf{G}(3) \ltimes \mathfrak{g}(3)$, the tangent group of the inhomogeneous Galilean group $\mathbf{G}(3)$. We define a novel preintegration error that geometrically couples the navigation states and the bias leading to lower linearization error. Our method improves in consistency compared to existing preintegration approaches which treat IMU biases as a separate state-space. Extensive validation against state-of-the-art methods, both in simulation and with real-world IMU data, implementation in the Lie++ library, and open-sourcing of the code are provided.

UVIO: An UWB-Aided Visual-Inertial Odometry Framework with Bias-Compensated Anchors Initialization

This paper introduces UVIO, a multi-sensor framework that leverages Ultra Wide Band (UWB) technology and Visual-Inertial Odometry (VIO) to provide robust and low-drift localization. In order to include range measurements in state estimation, the position of the UWB anchors must be known. This study proposes a multi-step initialization procedure to map multiple unknown anchors by an Unmanned Aerial Vehicle (UAV), in a fully autonomous fashion. To address the limitations of initializing UWB anchors via a random trajectory, this paper uses the Geometric Dilution of Precision (GDOP) as a measure of optimality in anchor position estimation, to compute a set of optimal waypoints and synthesize a trajectory that minimizes the mapping uncertainty. After the initialization is complete, the range measurements from multiple anchors, including measurement biases, are tightly integrated into the VIO system. While in range of the initialized anchors, the VIO drift in position and heading is eliminated. The effectiveness of UVIO and our initialization procedure has been validated through a series of simulations and real-world experiments.