Shengbo Gong
Scalable Graph Condensation with Evolving Capabilities
Feb 24, 2025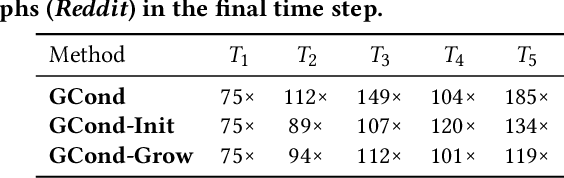
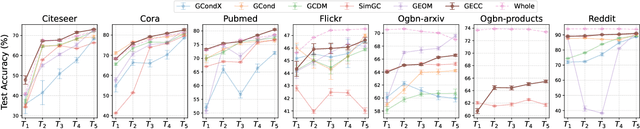
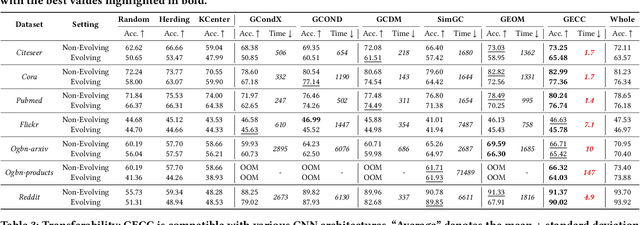
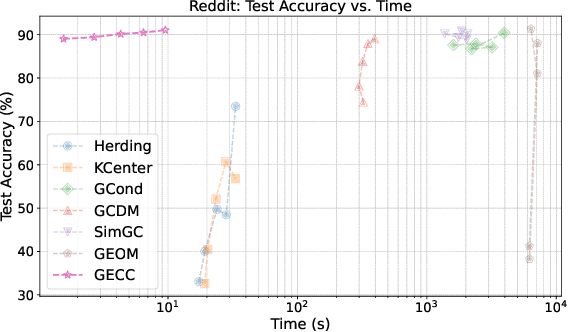
Abstract:Graph data has become a pivotal modality due to its unique ability to model relational datasets. However, real-world graph data continues to grow exponentially, resulting in a quadratic increase in the complexity of most graph algorithms as graph sizes expand. Although graph condensation (GC) methods have been proposed to address these scalability issues, existing approaches often treat the training set as static, overlooking the evolving nature of real-world graph data. This limitation leads to inefficiencies when condensing growing training sets. In this paper, we introduce GECC (Graph Evolving Clustering Condensation), a scalable graph condensation method designed to handle large-scale and evolving graph data. GECC employs a traceable and efficient approach by performing class-wise clustering on aggregated features. Furthermore, it can inherits previous condensation results as clustering centroids when the condensed graph expands, thereby attaining an evolving capability. This methodology is supported by robust theoretical foundations and demonstrates superior empirical performance. Comprehensive experiments show that GECC achieves better performance than most state-of-the-art graph condensation methods while delivering an around 1,000x speedup on large datasets.
GC-Bench: A Benchmark Framework for Graph Condensation with New Insights
Jun 24, 2024



Abstract:Graph condensation (GC) is an emerging technique designed to learn a significantly smaller graph that retains the essential information of the original graph. This condensed graph has shown promise in accelerating graph neural networks while preserving performance comparable to those achieved with the original, larger graphs. Additionally, this technique facilitates downstream applications such as neural architecture search and enhances our understanding of redundancy in large graphs. Despite the rapid development of GC methods, a systematic evaluation framework remains absent, which is necessary to clarify the critical designs for particular evaluative aspects. Furthermore, several meaningful questions have not been investigated, such as whether GC inherently preserves certain graph properties and offers robustness even without targeted design efforts. In this paper, we introduce GC-Bench, a comprehensive framework to evaluate recent GC methods across multiple dimensions and to generate new insights. Our experimental findings provide a deeper insights into the GC process and the characteristics of condensed graphs, guiding future efforts in enhancing performance and exploring new applications. Our code is available at \url{https://github.com/Emory-Melody/GraphSlim/tree/main/benchmark}.
A Comprehensive Survey on Graph Reduction: Sparsification, Coarsening, and Condensation
Feb 07, 2024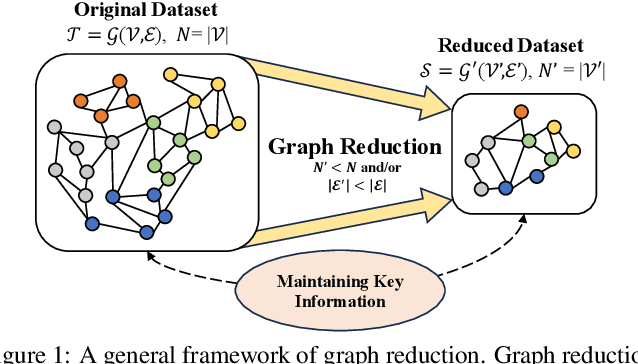

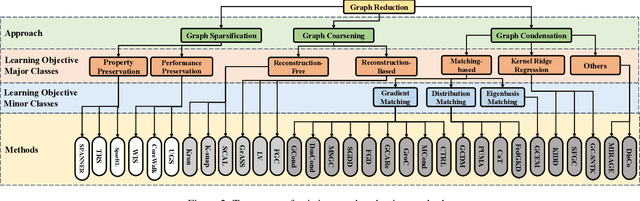

Abstract:Many real-world datasets can be naturally represented as graphs, spanning a wide range of domains. However, the increasing complexity and size of graph datasets present significant challenges for analysis and computation. In response, graph reduction techniques have gained prominence for simplifying large graphs while preserving essential properties. In this survey, we aim to provide a comprehensive understanding of graph reduction methods, including graph sparsification, graph coarsening, and graph condensation. Specifically, we establish a unified definition for these methods and introduce a hierarchical taxonomy to categorize the challenges they address. Our survey then systematically reviews the technical details of these methods and emphasizes their practical applications across diverse scenarios. Furthermore, we outline critical research directions to ensure the continued effectiveness of graph reduction techniques, as well as provide a comprehensive paper list at https://github.com/ChandlerBang/awesome-graph-reduction. We hope this survey will bridge literature gaps and propel the advancement of this promising field.
PathMLP: Smooth Path Towards High-order Homophily
Jun 23, 2023



Abstract:Real-world graphs exhibit increasing heterophily, where nodes no longer tend to be connected to nodes with the same label, challenging the homophily assumption of classical graph neural networks (GNNs) and impeding their performance. Intriguingly, we observe that certain high-order information on heterophilous data exhibits high homophily, which motivates us to involve high-order information in node representation learning. However, common practices in GNNs to acquire high-order information mainly through increasing model depth and altering message-passing mechanisms, which, albeit effective to a certain extent, suffer from three shortcomings: 1) over-smoothing due to excessive model depth and propagation times; 2) high-order information is not fully utilized; 3) low computational efficiency. In this regard, we design a similarity-based path sampling strategy to capture smooth paths containing high-order homophily. Then we propose a lightweight model based on multi-layer perceptrons (MLP), named PathMLP, which can encode messages carried by paths via simple transformation and concatenation operations, and effectively learn node representations in heterophilous graphs through adaptive path aggregation. Extensive experiments demonstrate that our method outperforms baselines on 16 out of 20 datasets, underlining its effectiveness and superiority in alleviating the heterophily problem. In addition, our method is immune to over-smoothing and has high computational efficiency.
Clarify Confused Nodes Through Separated Learning
Jun 04, 2023



Abstract:Graph neural networks (GNNs) have achieved remarkable advances in graph-oriented tasks. However, real-world graphs invariably contain a certain proportion of heterophilous nodes, challenging the homophily assumption of classical GNNs and hindering their performance. Most existing studies continue to design generic models with shared weights between heterophilous and homophilous nodes. Despite the incorporation of high-order message or multi-channel architectures, these efforts often fall short. A minority of studies attempt to train different node groups separately, but suffering from inappropriate separation metric and low efficiency. In this paper, we first propose a new metric, termed Neighborhood Confusion (NC), to facilitate a more reliable separation of nodes. We observe that node groups with different levels of NC values exhibit certain differences in intra-group accuracy and visualized embeddings. These pave a way for Neighborhood Confusion-guided Graph Convolutional Network (NCGCN), in which nodes are grouped by their NC values and accept intra-group weight sharing and message passing. Extensive experiments on both homophilous and heterophilous benchmarks demonstrate that NCGCN can effectively separate nodes and offers significant performance improvement compared to latest methods.
Neighborhood Homophily-Guided Graph Convolutional Network
Jan 24, 2023



Abstract:Graph neural networks (GNNs) have achieved remarkable advances in graph-oriented tasks. However, many real-world graphs contain heterophily or low homophily, challenging the homophily assumption of classical GNNs and resulting in low performance. Although many studies have emerged to improve the universality of GNNs, they rarely consider the label reuse and the correlation of their proposed metrics and models. In this paper, we first design a new metric, named Neighborhood Homophily (\textit{NH}), to measure the label complexity or purity in the neighborhood of nodes. Furthermore, we incorporate this metric into the classical graph convolutional network (GCN) architecture and propose \textbf{N}eighborhood \textbf{H}omophily-\textbf{G}uided \textbf{G}raph \textbf{C}onvolutional \textbf{N}etwork (\textbf{NHGCN}). In this framework, nodes are grouped by estimated \textit{NH} values to achieve intra-group weight sharing during message propagation and aggregation. Then the generated node predictions are used to estimate and update new \textit{NH} values. The two processes of metric estimation and model inference are alternately optimized to achieve better node classification. Extensive experiments on both homophilous and heterophilous benchmarks demonstrate that \textbf{NHGCN} achieves state-of-the-art overall performance on semi-supervised node classification for the universality problem.
Cross Cryptocurrency Relationship Mining for Bitcoin Price Prediction
Apr 28, 2022



Abstract:Blockchain finance has become a part of the world financial system, most typically manifested in the attention to the price of Bitcoin. However, a great deal of work is still limited to using technical indicators to capture Bitcoin price fluctuation, with little consideration of historical relationships and interactions between related cryptocurrencies. In this work, we propose a generic Cross-Cryptocurrency Relationship Mining module, named C2RM, which can effectively capture the synchronous and asynchronous impact factors between Bitcoin and related Altcoins. Specifically, we utilize the Dynamic Time Warping algorithm to extract the lead-lag relationship, yielding Lead-lag Variance Kernel, which will be used for aggregating the information of Altcoins to form relational impact factors. Comprehensive experimental results demonstrate that our C2RM can help existing price prediction methods achieve significant performance improvement, suggesting the effectiveness of Cross-Cryptocurrency interactions on benefitting Bitcoin price prediction.
Graph Modularity: Towards Understanding the Cross-Layer Transition of Feature Representations in Deep Neural Networks
Nov 24, 2021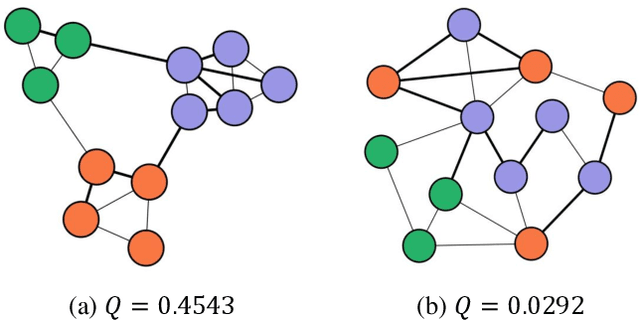
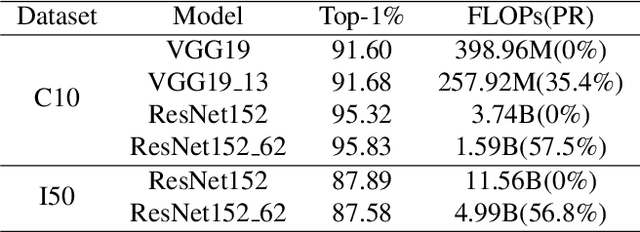
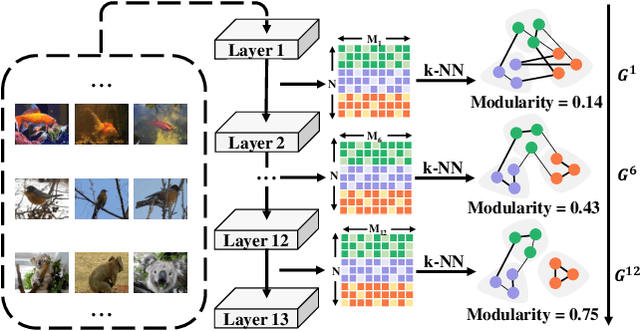
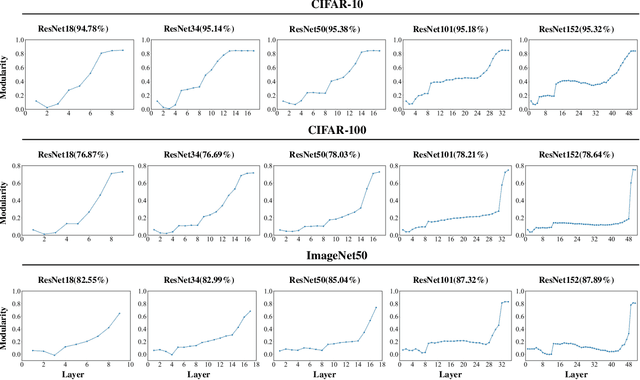
Abstract:There are good arguments to support the claim that feature representations eventually transition from general to specific in deep neural networks (DNNs), but this transition remains relatively underexplored. In this work, we move a tiny step towards understanding the transition of feature representations. We first characterize this transition by analyzing the class separation in intermediate layers, and next model the process of class separation as community evolution in dynamic graphs. Then, we introduce modularity, a common metric in graph theory, to quantify the evolution of communities. We find that modularity tends to rise as the layer goes deeper, but descends or reaches a plateau at particular layers. Through an asymptotic analysis, we show that modularity can provide quantitative analysis of the transition of the feature representations. With the insight on feature representations, we demonstrate that modularity can also be used to identify and locate redundant layers in DNNs, which provides theoretical guidance for layer pruning. Based on this inspiring finding, we propose a layer-wise pruning method based on modularity. Further experiments show that our method can prune redundant layers with minimal impact on performance. The codes are available at https://github.com/yaolu-zjut/Dynamic-Graphs-Construction.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge