Graph Modularity: Towards Understanding the Cross-Layer Transition of Feature Representations in Deep Neural Networks

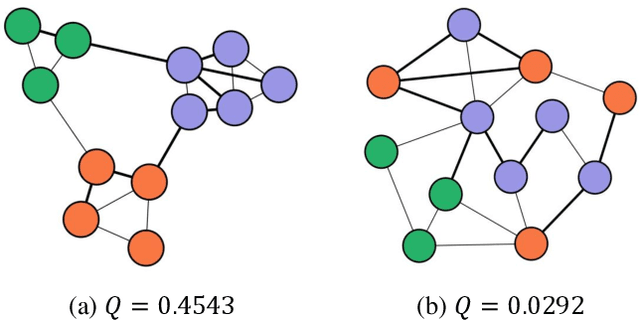
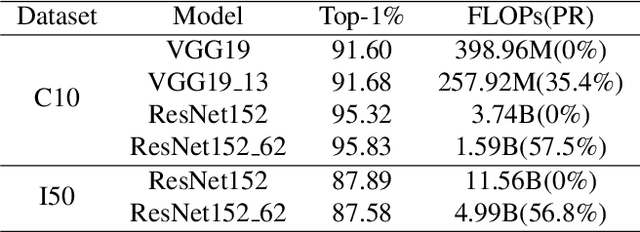
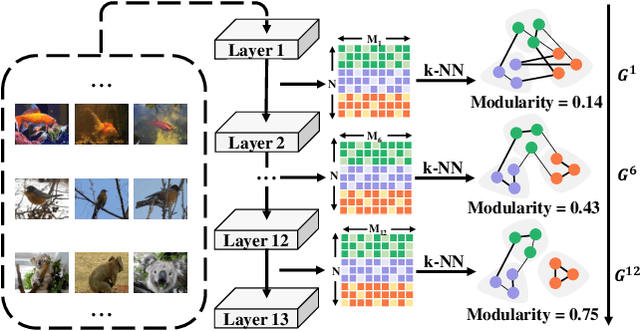
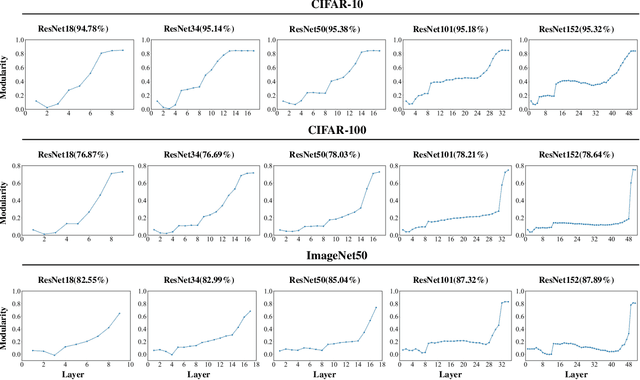
There are good arguments to support the claim that feature representations eventually transition from general to specific in deep neural networks (DNNs), but this transition remains relatively underexplored. In this work, we move a tiny step towards understanding the transition of feature representations. We first characterize this transition by analyzing the class separation in intermediate layers, and next model the process of class separation as community evolution in dynamic graphs. Then, we introduce modularity, a common metric in graph theory, to quantify the evolution of communities. We find that modularity tends to rise as the layer goes deeper, but descends or reaches a plateau at particular layers. Through an asymptotic analysis, we show that modularity can provide quantitative analysis of the transition of the feature representations. With the insight on feature representations, we demonstrate that modularity can also be used to identify and locate redundant layers in DNNs, which provides theoretical guidance for layer pruning. Based on this inspiring finding, we propose a layer-wise pruning method based on modularity. Further experiments show that our method can prune redundant layers with minimal impact on performance. The codes are available at https://github.com/yaolu-zjut/Dynamic-Graphs-Construction.