Surrogate Gap Minimization Improves Sharpness-Aware Training

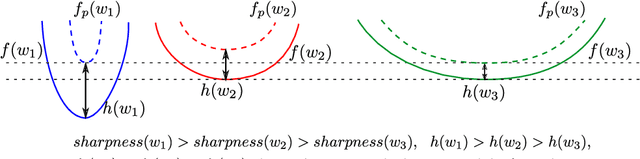
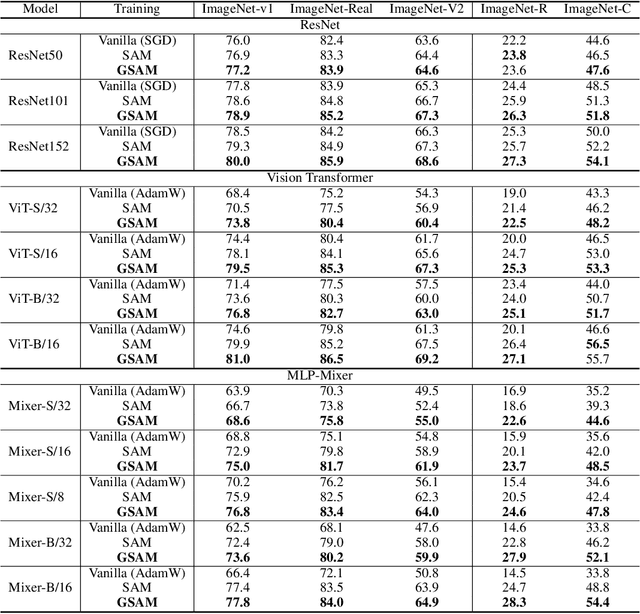
The recently proposed Sharpness-Aware Minimization (SAM) improves generalization by minimizing a \textit{perturbed loss} defined as the maximum loss within a neighborhood in the parameter space. However, we show that both sharp and flat minima can have a low perturbed loss, implying that SAM does not always prefer flat minima. Instead, we define a \textit{surrogate gap}, a measure equivalent to the dominant eigenvalue of Hessian at a local minimum when the radius of the neighborhood (to derive the perturbed loss) is small. The surrogate gap is easy to compute and feasible for direct minimization during training. Based on the above observations, we propose Surrogate \textbf{G}ap Guided \textbf{S}harpness-\textbf{A}ware \textbf{M}inimization (GSAM), a novel improvement over SAM with negligible computation overhead. Conceptually, GSAM consists of two steps: 1) a gradient descent like SAM to minimize the perturbed loss, and 2) an \textit{ascent} step in the \textit{orthogonal} direction (after gradient decomposition) to minimize the surrogate gap and yet not affect the perturbed loss. GSAM seeks a region with both small loss (by step 1) and low sharpness (by step 2), giving rise to a model with high generalization capabilities. Theoretically, we show the convergence of GSAM and provably better generalization than SAM. Empirically, GSAM consistently improves generalization (e.g., +3.2\% over SAM and +5.4\% over AdamW on ImageNet top-1 accuracy for ViT-B/32). Code is released at \url{ https://sites.google.com/view/gsam-iclr22/home}.

Momentum Centering and Asynchronous Update for Adaptive Gradient Methods

We propose ACProp (Asynchronous-centering-Prop), an adaptive optimizer which combines centering of second momentum and asynchronous update (e.g. for $t$-th update, denominator uses information up to step $t-1$, while numerator uses gradient at $t$-th step). ACProp has both strong theoretical properties and empirical performance. With the example by Reddi et al. (2018), we show that asynchronous optimizers (e.g. AdaShift, ACProp) have weaker convergence condition than synchronous optimizers (e.g. Adam, RMSProp, AdaBelief); within asynchronous optimizers, we show that centering of second momentum further weakens the convergence condition. We demonstrate that ACProp has a convergence rate of $O(\frac{1}{\sqrt{T}})$ for the stochastic non-convex case, which matches the oracle rate and outperforms the $O(\frac{logT}{\sqrt{T}})$ rate of RMSProp and Adam. We validate ACProp in extensive empirical studies: ACProp outperforms both SGD and other adaptive optimizers in image classification with CNN, and outperforms well-tuned adaptive optimizers in the training of various GAN models, reinforcement learning and transformers. To sum up, ACProp has good theoretical properties including weak convergence condition and optimal convergence rate, and strong empirical performance including good generalization like SGD and training stability like Adam. We provide the implementation at https://github.com/juntang-zhuang/ACProp-Optimizer.

MALI: A memory efficient and reverse accurate integrator for Neural ODEs

Neural ordinary differential equations (Neural ODEs) are a new family of deep-learning models with continuous depth. However, the numerical estimation of the gradient in the continuous case is not well solved: existing implementations of the adjoint method suffer from inaccuracy in reverse-time trajectory, while the naive method and the adaptive checkpoint adjoint method (ACA) have a memory cost that grows with integration time. In this project, based on the asynchronous leapfrog (ALF) solver, we propose the Memory-efficient ALF Integrator (MALI), which has a constant memory cost \textit{w.r.t} number of solver steps in integration similar to the adjoint method, and guarantees accuracy in reverse-time trajectory (hence accuracy in gradient estimation). We validate MALI in various tasks: on image recognition tasks, to our knowledge, MALI is the first to enable feasible training of a Neural ODE on ImageNet and outperform a well-tuned ResNet, while existing methods fail due to either heavy memory burden or inaccuracy; for time series modeling, MALI significantly outperforms the adjoint method; and for continuous generative models, MALI achieves new state-of-the-art performance. We provide a pypi package at \url{https://jzkay12.github.io/TorchDiffEqPack/}

Multiple-shooting adjoint method for whole-brain dynamic causal modeling

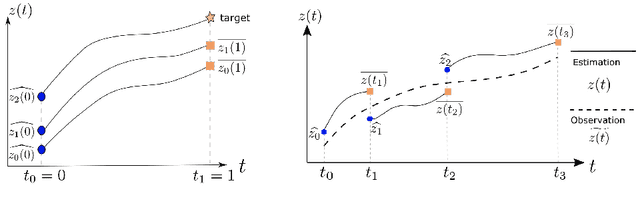
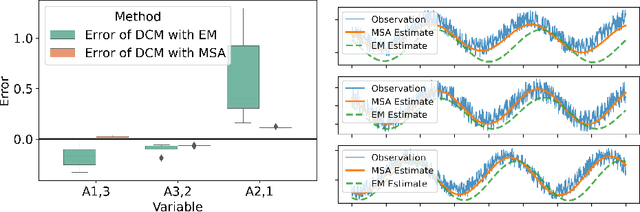
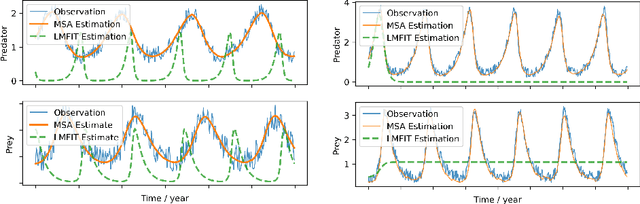
Dynamic causal modeling (DCM) is a Bayesian framework to infer directed connections between compartments, and has been used to describe the interactions between underlying neural populations based on functional neuroimaging data. DCM is typically analyzed with the expectation-maximization (EM) algorithm. However, because the inversion of a large-scale continuous system is difficult when noisy observations are present, DCM by EM is typically limited to a small number of compartments ($<10$). Another drawback with the current method is its complexity; when the forward model changes, the posterior mean changes, and we need to re-derive the algorithm for optimization. In this project, we propose the Multiple-Shooting Adjoint (MSA) method to address these limitations. MSA uses the multiple-shooting method for parameter estimation in ordinary differential equations (ODEs) under noisy observations, and is suitable for large-scale systems such as whole-brain analysis in functional MRI (fMRI). Furthermore, MSA uses the adjoint method for accurate gradient estimation in the ODE; since the adjoint method is generic, MSA is a generic method for both linear and non-linear systems, and does not require re-derivation of the algorithm as in EM. We validate MSA in extensive experiments: 1) in toy examples with both linear and non-linear models, we show that MSA achieves better accuracy in parameter value estimation than EM; furthermore, MSA can be successfully applied to large systems with up to 100 compartments; and 2) using real fMRI data, we apply MSA to the estimation of the whole-brain effective connectome and show improved classification of autism spectrum disorder (ASD) vs. control compared to using the functional connectome. The package is provided \url{https://jzkay12.github.io/TorchDiffEqPack}

AdaBelief Optimizer: Adapting Stepsizes by the Belief in Observed Gradients

Most popular optimizers for deep learning can be broadly categorized as adaptive methods (e.g. Adam) and accelerated schemes (e.g. stochastic gradient descent (SGD) with momentum). For many models such as convolutional neural networks (CNNs), adaptive methods typically converge faster but generalize worse compared to SGD; for complex settings such as generative adversarial networks (GANs), adaptive methods are typically the default because of their stability.We propose AdaBelief to simultaneously achieve three goals: fast convergence as in adaptive methods, good generalization as in SGD, and training stability. The intuition for AdaBelief is to adapt the stepsize according to the "belief" in the current gradient direction. Viewing the exponential moving average (EMA) of the noisy gradient as the prediction of the gradient at the next time step, if the observed gradient greatly deviates from the prediction, we distrust the current observation and take a small step; if the observed gradient is close to the prediction, we trust it and take a large step. We validate AdaBelief in extensive experiments, showing that it outperforms other methods with fast convergence and high accuracy on image classification and language modeling. Specifically, on ImageNet, AdaBelief achieves comparable accuracy to SGD. Furthermore, in the training of a GAN on Cifar10, AdaBelief demonstrates high stability and improves the quality of generated samples compared to a well-tuned Adam optimizer. Code is available at https://github.com/juntang-zhuang/Adabelief-Optimizer

Adaptive Checkpoint Adjoint Method for Gradient Estimation in Neural ODE

Neural ordinary differential equations (NODEs) have recently attracted increasing attention; however, their empirical performance on benchmark tasks (e.g. image classification) are significantly inferior to discrete-layer models. We demonstrate an explanation for their poorer performance is the inaccuracy of existing gradient estimation methods: the adjoint method has numerical errors in reverse-mode integration; the naive method directly back-propagates through ODE solvers, but suffers from a redundantly deep computation graph when searching for the optimal stepsize. We propose the Adaptive Checkpoint Adjoint (ACA) method: in automatic differentiation, ACA applies a trajectory checkpoint strategy which records the forward-mode trajectory as the reverse-mode trajectory to guarantee accuracy; ACA deletes redundant components for shallow computation graphs; and ACA supports adaptive solvers. On image classification tasks, compared with the adjoint and naive method, ACA achieves half the error rate in half the training time; NODE trained with ACA outperforms ResNet in both accuracy and test-retest reliability. On time-series modeling, ACA outperforms competing methods. Finally, in an example of the three-body problem, we show NODE with ACA can incorporate physical knowledge to achieve better accuracy. We provide the PyTorch implementation of ACA: \url{https://github.com/juntang-zhuang/torch-ACA}.

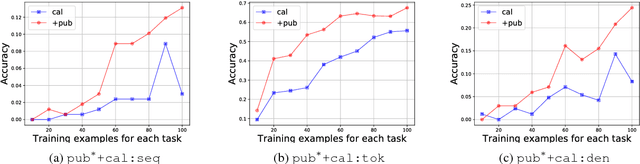
Zero-shot Transfer Learning for Semantic Parsing

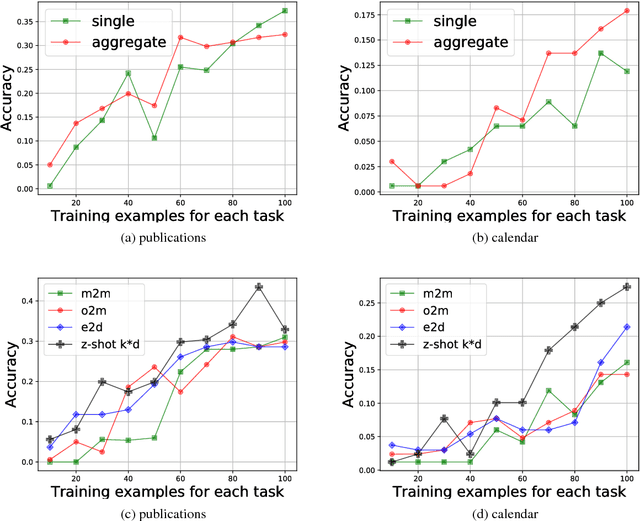
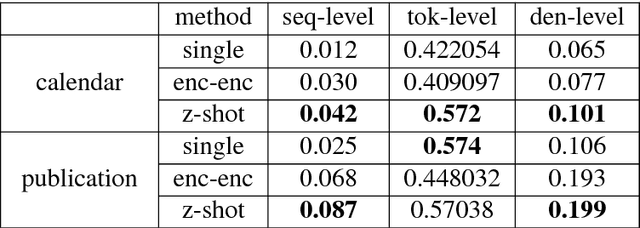
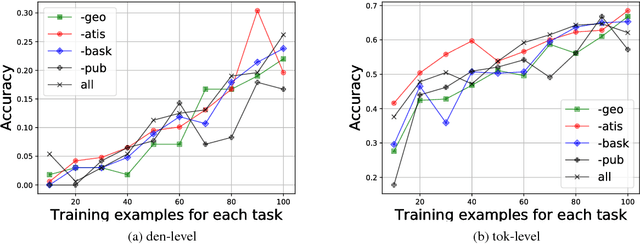
While neural networks have shown impressive performance on large datasets, applying these models to tasks where little data is available remains a challenging problem. In this paper we propose to use feature transfer in a zero-shot experimental setting on the task of semantic parsing. We first introduce a new method for learning the shared space between multiple domains based on the prediction of the domain label for each example. Our experiments support the superiority of this method in a zero-shot experimental setting in terms of accuracy metrics compared to state-of-the-art techniques. In the second part of this paper we study the impact of individual domains and examples on semantic parsing performance. We use influence functions to this aim and investigate the sensitivity of domain-label classification loss on each example. Our findings reveal that cross-domain adversarial attacks identify useful examples for training even from the domains the least similar to the target domain. Augmenting our training data with these influential examples further boosts our accuracy at both the token and the sequence level.

Sequence to Logic with Copy and Cache

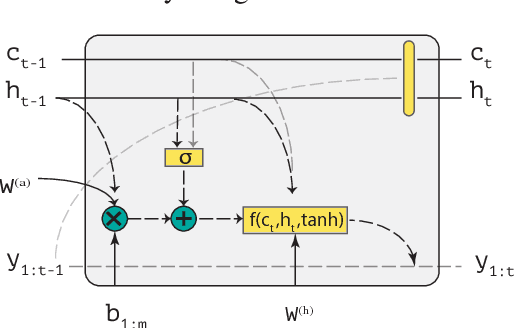
Generating logical form equivalents of human language is a fresh way to employ neural architectures where long short-term memory effectively captures dependencies in both encoder and decoder units. The logical form of the sequence usually preserves information from the natural language side in the form of similar tokens, and recently a copying mechanism has been proposed which increases the probability of outputting tokens from the source input through decoding. In this paper we propose a caching mechanism as a more general form of the copying mechanism which also weighs all the words from the source vocabulary according to their relation to the current decoding context. Our results confirm that the proposed method achieves improvements in sequence/token-level accuracy on sequence to logical form tasks. Further experiments on cross-domain adversarial attacks show substantial improvements when using the most influential examples of other domains for training.

A new approach to Laplacian solvers and flow problems

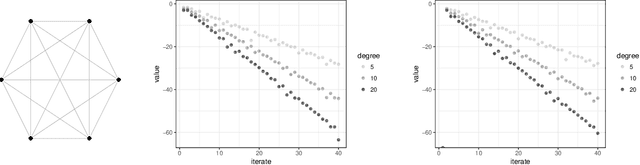
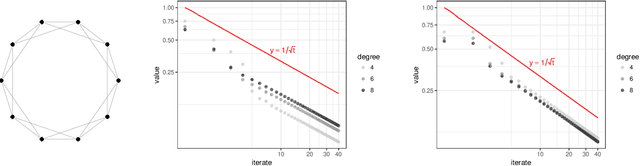
This paper investigates message-passing algorithms for solving systems of linear equations in the Laplacian matrices of graphs and to compute electric flows. These two problems are fundamental primitives that arise in several domains such as computer science, electrical engineering, operations research, and machine learning. Despite the extensive literature on approximately solving these problems in quasi-linear time, the algorithms that have been proposed are typically centralized and involve multiple graph theoretic constructions or sampling mechanisms that make them difficult to implement and analyze. On the other hand, message-passing routines are distributed, simple, and easy to implement. In this paper we establish a framework to analyze message-passing algorithms to solve voltage and flow problems. We characterize the error committed by the algorithms in d-regular graphs with equal weights. We show that the convergence of the algorithms is controlled by the total variation distance between the distributions of non-backtracking random walks that start from neighbor nodes. More broadly, our analysis of message-passing introduces new insights to address generic optimization problems with constraints.

Scale-free network optimization: foundations and algorithms

We investigate the fundamental principles that drive the development of scalable algorithms for network optimization. Despite the significant amount of work on parallel and decentralized algorithms in the optimization community, the methods that have been proposed typically rely on strict separability assumptions for objective function and constraints. Beside sparsity, these methods typically do not exploit the strength of the interaction between variables in the system. We propose a notion of correlation in constrained optimization that is based on the sensitivity of the optimal solution upon perturbations of the constraints. We develop a general theory of sensitivity of optimizers the extends beyond the infinitesimal setting. We present instances in network optimization where the correlation decays exponentially fast with respect to the natural distance in the network, and we design algorithms that can exploit this decay to yield dimension-free optimization. Our results are the first of their kind, and open new possibilities in the theory of local algorithms.