Surrogate Gap Minimization Improves Sharpness-Aware Training
Paper and Code
Mar 19, 2022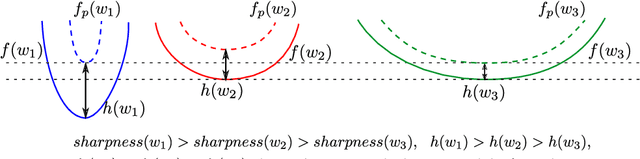
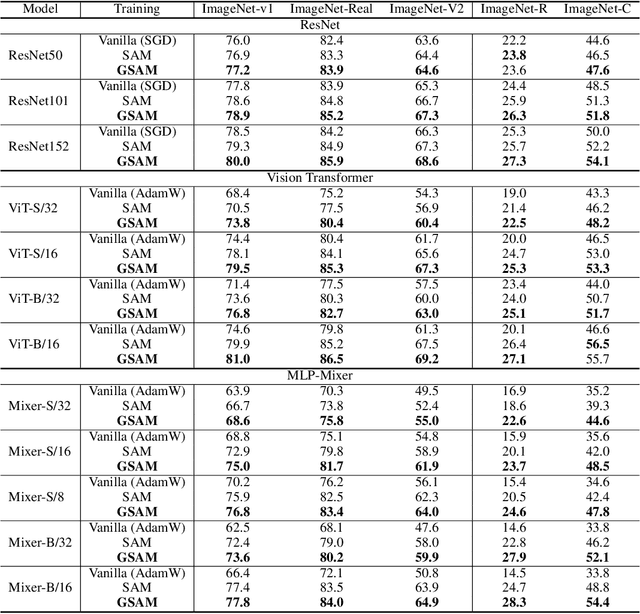


The recently proposed Sharpness-Aware Minimization (SAM) improves generalization by minimizing a \textit{perturbed loss} defined as the maximum loss within a neighborhood in the parameter space. However, we show that both sharp and flat minima can have a low perturbed loss, implying that SAM does not always prefer flat minima. Instead, we define a \textit{surrogate gap}, a measure equivalent to the dominant eigenvalue of Hessian at a local minimum when the radius of the neighborhood (to derive the perturbed loss) is small. The surrogate gap is easy to compute and feasible for direct minimization during training. Based on the above observations, we propose Surrogate \textbf{G}ap Guided \textbf{S}harpness-\textbf{A}ware \textbf{M}inimization (GSAM), a novel improvement over SAM with negligible computation overhead. Conceptually, GSAM consists of two steps: 1) a gradient descent like SAM to minimize the perturbed loss, and 2) an \textit{ascent} step in the \textit{orthogonal} direction (after gradient decomposition) to minimize the surrogate gap and yet not affect the perturbed loss. GSAM seeks a region with both small loss (by step 1) and low sharpness (by step 2), giving rise to a model with high generalization capabilities. Theoretically, we show the convergence of GSAM and provably better generalization than SAM. Empirically, GSAM consistently improves generalization (e.g., +3.2\% over SAM and +5.4\% over AdamW on ImageNet top-1 accuracy for ViT-B/32). Code is released at \url{ https://sites.google.com/view/gsam-iclr22/home}.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge