Low-Rank-Modulated Functa: Exploring the Latent Space of Implicit Neural Representations for Interpretable Ultrasound Video Analysis

Implicit neural representations (INRs) have emerged as a powerful framework for continuous image representation learning. In Functa-based approaches, each image is encoded as a latent modulation vector that conditions a shared INR, enabling strong reconstruction performance. However, the structure and interpretability of the corresponding latent spaces remain largely unexplored. In this work, we investigate the latent space of Functa-based models for ultrasound videos and propose Low-Rank-Modulated Functa (LRM-Functa), a novel architecture that enforces a low-rank adaptation of modulation vectors in the time-resolved latent space. When applied to cardiac ultrasound, the resulting latent space exhibits clearly structured periodic trajectories, facilitating visualization and interpretability of temporal patterns. The latent space can be traversed to sample novel frames, revealing smooth transitions along the cardiac cycle, and enabling direct readout of end-diastolic (ED) and end-systolic (ES) frames without additional model training. We show that LRM-Functa outperforms prior methods in unsupervised ED and ES frame detection, while compressing each video frame to as low as rank k=2 without sacrificing competitive downstream performance on ejection fraction prediction. Evaluations on out-of-distribution frame selection in a cardiac point-of-care dataset, as well as on lung ultrasound for B-line classification, demonstrate the generalizability of our approach. Overall, LRM-Functa provides a compact, interpretable, and generalizable framework for ultrasound video analysis. The code is available at https://github.com/JuliaWolleb/LRM_Functa.

VidFuncta: Towards Generalizable Neural Representations for Ultrasound Videos

Ultrasound is widely used in clinical care, yet standard deep learning methods often struggle with full video analysis due to non-standardized acquisition and operator bias. We offer a new perspective on ultrasound video analysis through implicit neural representations (INRs). We build on Functa, an INR framework in which each image is represented by a modulation vector that conditions a shared neural network. However, its extension to the temporal domain of medical videos remains unexplored. To address this gap, we propose VidFuncta, a novel framework that leverages Functa to encode variable-length ultrasound videos into compact, time-resolved representations. VidFuncta disentangles each video into a static video-specific vector and a sequence of time-dependent modulation vectors, capturing both temporal dynamics and dataset-level redundancies. Our method outperforms 2D and 3D baselines on video reconstruction and enables downstream tasks to directly operate on the learned 1D modulation vectors. We validate VidFuncta on three public ultrasound video datasets -- cardiac, lung, and breast -- and evaluate its downstream performance on ejection fraction prediction, B-line detection, and breast lesion classification. These results highlight the potential of VidFuncta as a generalizable and efficient representation framework for ultrasound videos. Our code is publicly available under https://github.com/JuliaWolleb/VidFuncta_public.

Multiple-shooting adjoint method for whole-brain dynamic causal modeling

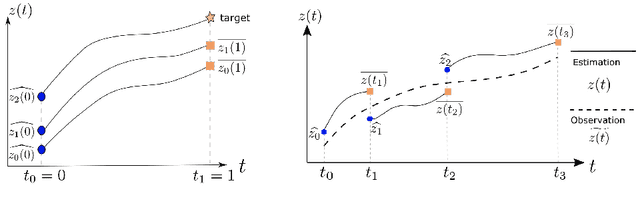
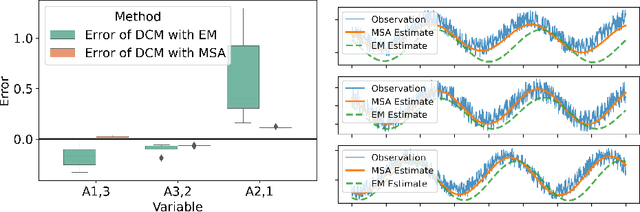
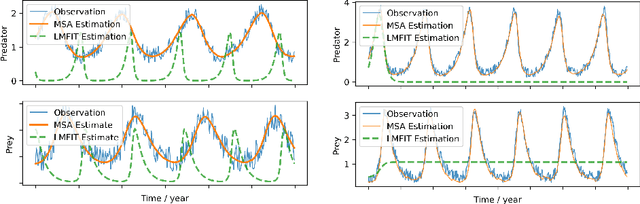
Dynamic causal modeling (DCM) is a Bayesian framework to infer directed connections between compartments, and has been used to describe the interactions between underlying neural populations based on functional neuroimaging data. DCM is typically analyzed with the expectation-maximization (EM) algorithm. However, because the inversion of a large-scale continuous system is difficult when noisy observations are present, DCM by EM is typically limited to a small number of compartments ($<10$). Another drawback with the current method is its complexity; when the forward model changes, the posterior mean changes, and we need to re-derive the algorithm for optimization. In this project, we propose the Multiple-Shooting Adjoint (MSA) method to address these limitations. MSA uses the multiple-shooting method for parameter estimation in ordinary differential equations (ODEs) under noisy observations, and is suitable for large-scale systems such as whole-brain analysis in functional MRI (fMRI). Furthermore, MSA uses the adjoint method for accurate gradient estimation in the ODE; since the adjoint method is generic, MSA is a generic method for both linear and non-linear systems, and does not require re-derivation of the algorithm as in EM. We validate MSA in extensive experiments: 1) in toy examples with both linear and non-linear models, we show that MSA achieves better accuracy in parameter value estimation than EM; furthermore, MSA can be successfully applied to large systems with up to 100 compartments; and 2) using real fMRI data, we apply MSA to the estimation of the whole-brain effective connectome and show improved classification of autism spectrum disorder (ASD) vs. control compared to using the functional connectome. The package is provided \url{https://jzkay12.github.io/TorchDiffEqPack}

AdaBelief Optimizer: Adapting Stepsizes by the Belief in Observed Gradients

Most popular optimizers for deep learning can be broadly categorized as adaptive methods (e.g. Adam) and accelerated schemes (e.g. stochastic gradient descent (SGD) with momentum). For many models such as convolutional neural networks (CNNs), adaptive methods typically converge faster but generalize worse compared to SGD; for complex settings such as generative adversarial networks (GANs), adaptive methods are typically the default because of their stability.We propose AdaBelief to simultaneously achieve three goals: fast convergence as in adaptive methods, good generalization as in SGD, and training stability. The intuition for AdaBelief is to adapt the stepsize according to the "belief" in the current gradient direction. Viewing the exponential moving average (EMA) of the noisy gradient as the prediction of the gradient at the next time step, if the observed gradient greatly deviates from the prediction, we distrust the current observation and take a small step; if the observed gradient is close to the prediction, we trust it and take a large step. We validate AdaBelief in extensive experiments, showing that it outperforms other methods with fast convergence and high accuracy on image classification and language modeling. Specifically, on ImageNet, AdaBelief achieves comparable accuracy to SGD. Furthermore, in the training of a GAN on Cifar10, AdaBelief demonstrates high stability and improves the quality of generated samples compared to a well-tuned Adam optimizer. Code is available at https://github.com/juntang-zhuang/Adabelief-Optimizer

Adaptive Checkpoint Adjoint Method for Gradient Estimation in Neural ODE

Neural ordinary differential equations (NODEs) have recently attracted increasing attention; however, their empirical performance on benchmark tasks (e.g. image classification) are significantly inferior to discrete-layer models. We demonstrate an explanation for their poorer performance is the inaccuracy of existing gradient estimation methods: the adjoint method has numerical errors in reverse-mode integration; the naive method directly back-propagates through ODE solvers, but suffers from a redundantly deep computation graph when searching for the optimal stepsize. We propose the Adaptive Checkpoint Adjoint (ACA) method: in automatic differentiation, ACA applies a trajectory checkpoint strategy which records the forward-mode trajectory as the reverse-mode trajectory to guarantee accuracy; ACA deletes redundant components for shallow computation graphs; and ACA supports adaptive solvers. On image classification tasks, compared with the adjoint and naive method, ACA achieves half the error rate in half the training time; NODE trained with ACA outperforms ResNet in both accuracy and test-retest reliability. On time-series modeling, ACA outperforms competing methods. Finally, in an example of the three-body problem, we show NODE with ACA can incorporate physical knowledge to achieve better accuracy. We provide the PyTorch implementation of ACA: \url{https://github.com/juntang-zhuang/torch-ACA}.