A new approach to Laplacian solvers and flow problems

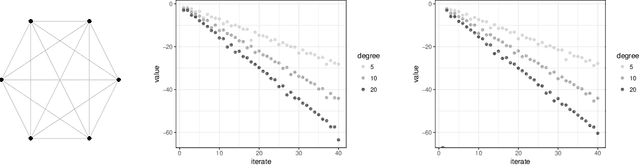
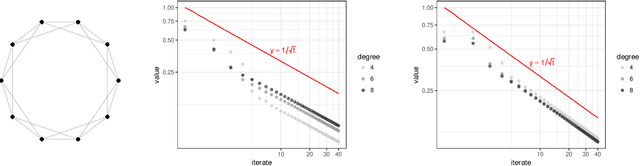
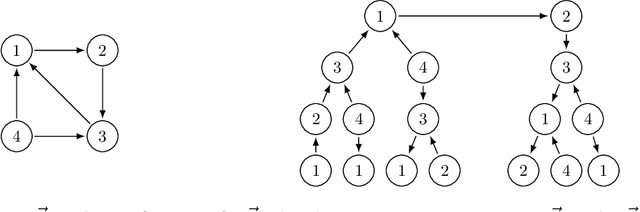
This paper investigates message-passing algorithms for solving systems of linear equations in the Laplacian matrices of graphs and to compute electric flows. These two problems are fundamental primitives that arise in several domains such as computer science, electrical engineering, operations research, and machine learning. Despite the extensive literature on approximately solving these problems in quasi-linear time, the algorithms that have been proposed are typically centralized and involve multiple graph theoretic constructions or sampling mechanisms that make them difficult to implement and analyze. On the other hand, message-passing routines are distributed, simple, and easy to implement. In this paper we establish a framework to analyze message-passing algorithms to solve voltage and flow problems. We characterize the error committed by the algorithms in d-regular graphs with equal weights. We show that the convergence of the algorithms is controlled by the total variation distance between the distributions of non-backtracking random walks that start from neighbor nodes. More broadly, our analysis of message-passing introduces new insights to address generic optimization problems with constraints.