Sahand Negahban
Tree-Projected Gradient Descent for Estimating Gradient-Sparse Parameters on Graphs
May 31, 2020


Abstract:We study estimation of a gradient-sparse parameter vector $\boldsymbol{\theta}^* \in \mathbb{R}^p$, having strong gradient-sparsity $s^*:=\|\nabla_G \boldsymbol{\theta}^*\|_0$ on an underlying graph $G$. Given observations $Z_1,\ldots,Z_n$ and a smooth, convex loss function $\mathcal{L}$ for which $\boldsymbol{\theta}^*$ minimizes the population risk $\mathbb{E}[\mathcal{L}(\boldsymbol{\theta};Z_1,\ldots,Z_n)]$, we propose to estimate $\boldsymbol{\theta}^*$ by a projected gradient descent algorithm that iteratively and approximately projects gradient steps onto spaces of vectors having small gradient-sparsity over low-degree spanning trees of $G$. We show that, under suitable restricted strong convexity and smoothness assumptions for the loss, the resulting estimator achieves the squared-error risk $\frac{s^*}{n} \log (1+\frac{p}{s^*})$ up to a multiplicative constant that is independent of $G$. In contrast, previous polynomial-time algorithms have only been shown to achieve this guarantee in more specialized settings, or under additional assumptions for $G$ and/or the sparsity pattern of $\nabla_G \boldsymbol{\theta}^*$. As applications of our general framework, we apply our results to the examples of linear models and generalized linear models with random design.
Alternating Linear Bandits for Online Matrix-Factorization Recommendation
Oct 22, 2018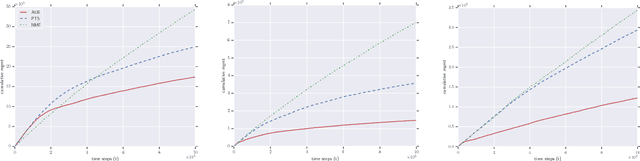
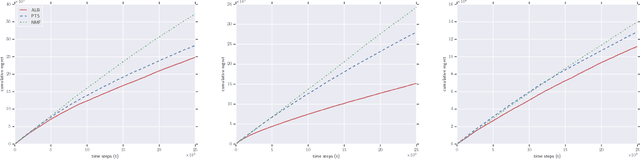
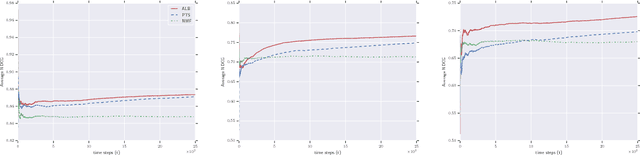
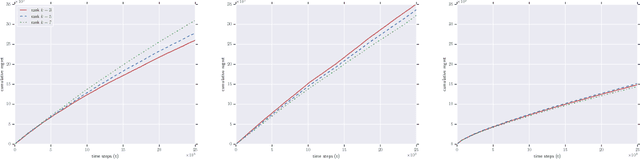
Abstract:We consider the problem of online collaborative filtering in the online setting, where items are recommended to the users over time. At each time step, the user (selected by the environment) consumes an item (selected by the agent) and provides a rating of the selected item. In this paper, we propose a novel algorithm for online matrix factorization recommendation that combines linear bandits and alternating least squares. In this formulation, the bandit feedback is equal to the difference between the ratings of the best and selected items. We evaluate the performance of the proposed algorithm over time using both cumulative regret and average cumulative NDCG. Simulation results over three synthetic datasets as well as three real-world datasets for online collaborative filtering indicate the superior performance of the proposed algorithm over two state-of-the-art online algorithms.
Deep supervised feature selection using Stochastic Gates
Oct 09, 2018



Abstract:In this study, we propose a novel non-parametric embedded feature selection method based on minimizing the $\ell_0$ norm of the vector of an indicator variable, whose point-wise product of an input selects a subset of features. Our approach relies on the continuous relaxation of Bernoulli distributions, which allows our model to learn the parameters of the approximate Bernoulli distributions via tractable methods. Using these tools we present a general neural network that simultaneously minimizes a loss function while selecting relevant features. We also provide an information-theoretic justification of incorporating Bernoulli distribution into our approach. Finally, we demonstrate the potential of the approach on synthetic and real-life applications.
Super-resolution estimation of cyclic arrival rates
Jun 05, 2018


Abstract:Exploiting the fact that most arrival processes exhibit cyclic behaviour, we propose a simple procedure for estimating the intensity of a nonhomogeneous Poisson process. The estimator is the super-resolution analogue to Shao 2010 and Shao & Lii 2011, which is a sum of $p$ sinusoids where $p$ and the frequency, amplitude, and phase of each wave are not known and need to be estimated. This results in an interpretable yet flexible specification that is suitable for use in modelling as well as in high resolution simulations. Our estimation procedure sits in between classic periodogram methods and atomic/total variation norm thresholding. Through a novel use of window functions in the point process domain, our approach attains super-resolution without semidefinite programming. Under suitable conditions, finite sample guarantees can be derived for our procedure. These resolve some open questions and expand existing results in spectral estimation literature.
Minimax Estimation of Bandable Precision Matrices
Oct 19, 2017
Abstract:The inverse covariance matrix provides considerable insight for understanding statistical models in the multivariate setting. In particular, when the distribution over variables is assumed to be multivariate normal, the sparsity pattern in the inverse covariance matrix, commonly referred to as the precision matrix, corresponds to the adjacency matrix representation of the Gauss-Markov graph, which encodes conditional independence statements between variables. Minimax results under the spectral norm have previously been established for covariance matrices, both sparse and banded, and for sparse precision matrices. We establish minimax estimation bounds for estimating banded precision matrices under the spectral norm. Our results greatly improve upon the existing bounds; in particular, we find that the minimax rate for estimating banded precision matrices matches that of estimating banded covariance matrices. The key insight in our analysis is that we are able to obtain barely-noisy estimates of $k \times k$ subblocks of the precision matrix by inverting slightly wider blocks of the empirical covariance matrix along the diagonal. Our theoretical results are complemented by experiments demonstrating the sharpness of our bounds.
Restricted Strong Convexity Implies Weak Submodularity
Oct 12, 2017
Abstract:We connect high-dimensional subset selection and submodular maximization. Our results extend the work of Das and Kempe (2011) from the setting of linear regression to arbitrary objective functions. For greedy feature selection, this connection allows us to obtain strong multiplicative performance bounds on several methods without statistical modeling assumptions. We also derive recovery guarantees of this form under standard assumptions. Our work shows that greedy algorithms perform within a constant factor from the best possible subset-selection solution for a broad class of general objective functions. Our methods allow a direct control over the number of obtained features as opposed to regularization parameters that only implicitly control sparsity. Our proof technique uses the concept of weak submodularity initially defined by Das and Kempe. We draw a connection between convex analysis and submodular set function theory which may be of independent interest for other statistical learning applications that have combinatorial structure.
Learning from Comparisons and Choices
Apr 24, 2017
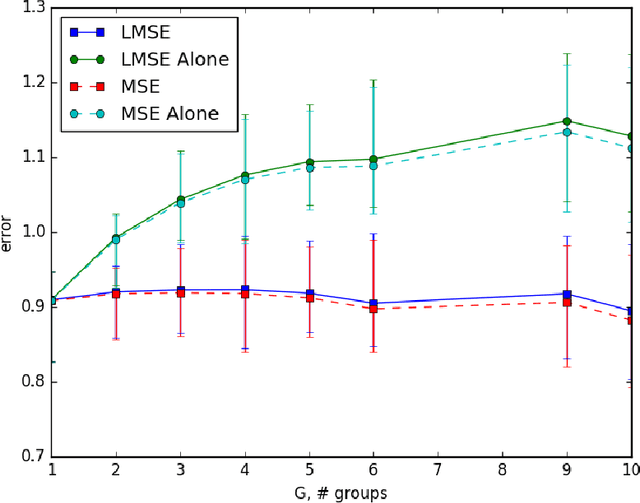
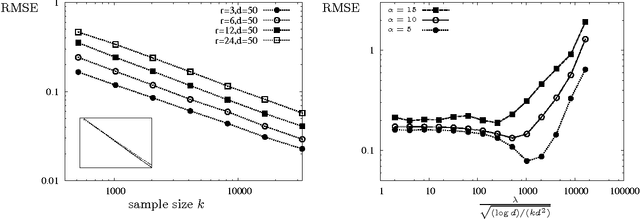
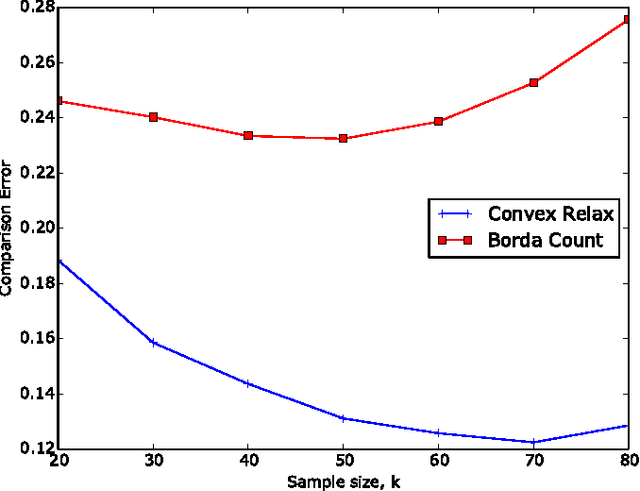
Abstract:When tracking user-specific online activities, each user's preference is revealed in the form of choices and comparisons. For example, a user's purchase history tracks her choices, i.e. which item was chosen among a subset of offerings. A user's comparisons are observed either explicitly as in movie ratings or implicitly as in viewing times of news articles. Given such individualized ordinal data, we address the problem of collaboratively learning representations of the users and the items. The learned features can be used to predict a user's preference of an unseen item to be used in recommendation systems. This also allows one to compute similarities among users and items to be used for categorization and search. Motivated by the empirical successes of the MultiNomial Logit (MNL) model in marketing and transportation, and also more recent successes in word embedding and crowdsourced image embedding, we pose this problem as learning the MNL model parameters that best explains the data. We propose a convex optimization for learning the MNL model, and show that it is minimax optimal up to a logarithmic factor by comparing its performance to a fundamental lower bound. This characterizes the minimax sample complexity of the problem, and proves that the proposed estimator cannot be improved upon other than by a logarithmic factor. Further, the analysis identifies how the accuracy depends on the topology of sampling via the spectrum of the sampling graph. This provides a guideline for designing surveys when one can choose which items are to be compared. This is accompanies by numerical simulations on synthetic and real datasets confirming our theoretical predictions.
Scalable Greedy Feature Selection via Weak Submodularity
Mar 08, 2017



Abstract:Greedy algorithms are widely used for problems in machine learning such as feature selection and set function optimization. Unfortunately, for large datasets, the running time of even greedy algorithms can be quite high. This is because for each greedy step we need to refit a model or calculate a function using the previously selected choices and the new candidate. Two algorithms that are faster approximations to the greedy forward selection were introduced recently ([Mirzasoleiman et al. 2013, 2015]). They achieve better performance by exploiting distributed computation and stochastic evaluation respectively. Both algorithms have provable performance guarantees for submodular functions. In this paper we show that divergent from previously held opinion, submodularity is not required to obtain approximation guarantees for these two algorithms. Specifically, we show that a generalized concept of weak submodularity suffices to give multiplicative approximation guarantees. Our result extends the applicability of these algorithms to a larger class of functions. Furthermore, we show that a bounded submodularity ratio can be used to provide data dependent bounds that can sometimes be tighter also for submodular functions. We empirically validate our work by showing superior performance of fast greedy approximations versus several established baselines on artificial and real datasets.
On Approximation Guarantees for Greedy Low Rank Optimization
Mar 08, 2017

Abstract:We provide new approximation guarantees for greedy low rank matrix estimation under standard assumptions of restricted strong convexity and smoothness. Our novel analysis also uncovers previously unknown connections between the low rank estimation and combinatorial optimization, so much so that our bounds are reminiscent of corresponding approximation bounds in submodular maximization. Additionally, we also provide statistical recovery guarantees. Finally, we present empirical comparison of greedy estimation with established baselines on two important real-world problems.
Understanding Adversarial Training: Increasing Local Stability of Neural Nets through Robust Optimization
Jan 16, 2016



Abstract:We propose a general framework for increasing local stability of Artificial Neural Nets (ANNs) using Robust Optimization (RO). We achieve this through an alternating minimization-maximization procedure, in which the loss of the network is minimized over perturbed examples that are generated at each parameter update. We show that adversarial training of ANNs is in fact robustification of the network optimization, and that our proposed framework generalizes previous approaches for increasing local stability of ANNs. Experimental results reveal that our approach increases the robustness of the network to existing adversarial examples, while making it harder to generate new ones. Furthermore, our algorithm improves the accuracy of the network also on the original test data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge