Boosted generalized normal distributions: Integrating machine learning with operations knowledge

Applications of machine learning (ML) techniques to operational settings often face two challenges: i) ML methods mostly provide point predictions whereas many operational problems require distributional information; and ii) They typically do not incorporate the extensive body of knowledge in the operations literature, particularly the theoretical and empirical findings that characterize specific distributions. We introduce a novel and rigorous methodology, the Boosted Generalized Normal Distribution ($b$GND), to address these challenges. The Generalized Normal Distribution (GND) encompasses a wide range of parametric distributions commonly encountered in operations, and $b$GND leverages gradient boosting with tree learners to flexibly estimate the parameters of the GND as functions of covariates. We establish $b$GND's statistical consistency, thereby extending this key property to special cases studied in the ML literature that lacked such guarantees. Using data from a large academic emergency department in the United States, we show that the distributional forecasting of patient wait and service times can be meaningfully improved by leveraging findings from the healthcare operations literature. Specifically, $b$GND performs 6% and 9% better than the distribution-agnostic ML benchmark used to forecast wait and service times respectively. Further analysis suggests that these improvements translate into a 9% increase in patient satisfaction and a 4% reduction in mortality for myocardial infarction patients. Our work underscores the importance of integrating ML with operations knowledge to enhance distributional forecasts.

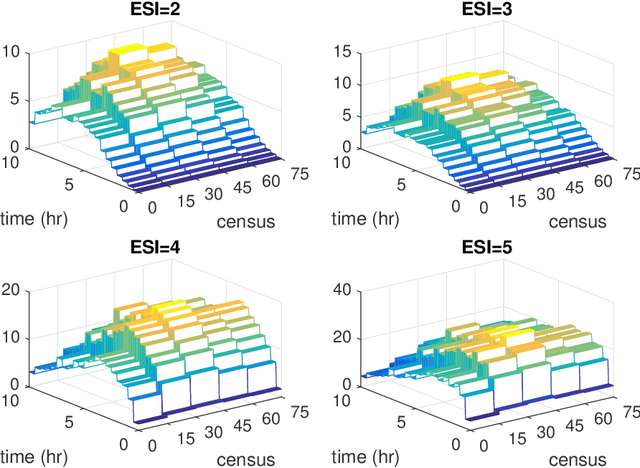
Real-time Mortality Prediction Using MIMIC-IV ICU Data Via Boosted Nonparametric Hazards

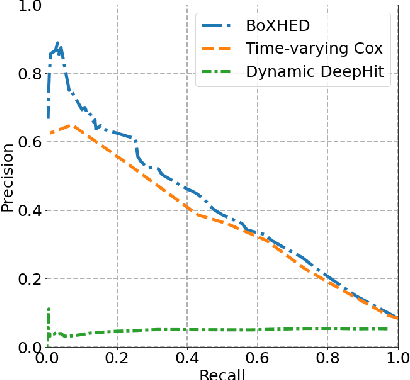
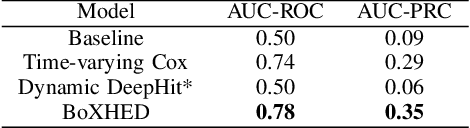
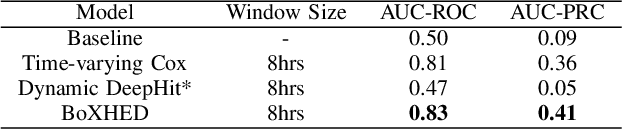
Electronic Health Record (EHR) systems provide critical, rich and valuable information at high frequency. One of the most exciting applications of EHR data is in developing a real-time mortality warning system with tools from survival analysis. However, most of the survival analysis methods used recently are based on (semi)parametric models using static covariates. These models do not take advantage of the information conveyed by the time-varying EHR data. In this work, we present an application of a highly scalable survival analysis method, BoXHED 2.0 to develop a real-time in-ICU mortality warning indicator based on the MIMIC IV data set. Importantly, BoXHED can incorporate time-dependent covariates in a fully nonparametric manner and is backed by theory. Our in-ICU mortality model achieves an AUC-PRC of 0.41 and AUC-ROC of 0.83 out of sample, demonstrating the benefit of real-time monitoring.

BoXHED 2.0: Scalable boosting of functional data in survival analysis

Modern applications of survival analysis increasingly involve time-dependent covariates, which constitute a form of functional data. Learning from functional data generally involves repeated evaluations of time integrals which is numerically expensive. In this work we propose a lightweight data preprocessing step that transforms functional data into nonfunctional data. Boosting implementations for nonfunctional data can then be used, whereby the required numerical integration comes for free as part of the training phase. We use this to develop BoXHED 2.0, a quantum leap over the tree-boosted hazard package BoXHED 1.0. BoXHED 2.0 extends BoXHED 1.0 to Aalen's multiplicative intensity model, which covers censoring schemes far beyond right-censoring and also supports recurrent events data. It is also massively scalable because of preprocessing and also because it borrows from the core components of XGBoost. BoXHED 2.0 supports the use of GPUs and multicore CPUs, and is available from GitHub: www.github.com/BoXHED.

BoXHED: Boosted eXact Hazard Estimator with Dynamic covariates

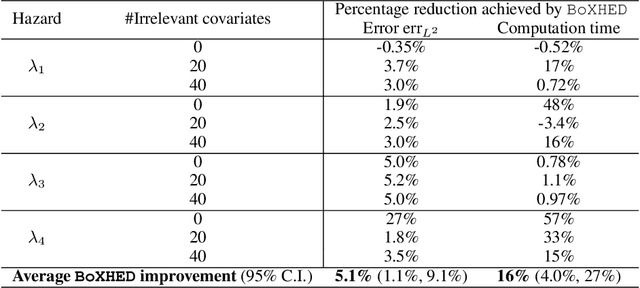
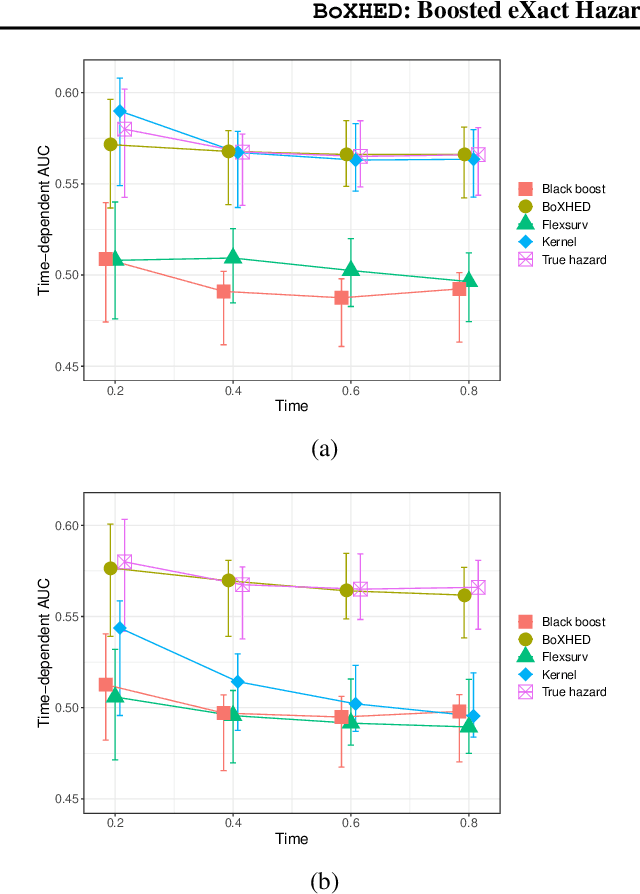
The proliferation of medical monitoring devices makes it possible to track health vitals at high frequency, enabling the development of dynamic health risk scores that change with the underlying readings. Survival analysis, in particular hazard estimation, is well-suited to analyzing this stream of data to predict disease onset as a function of the time-varying vitals. This paper introduces the software package BoXHED (pronounced 'box-head') for nonparametrically estimating hazard functions via gradient boosting. BoXHED 1.0 is a novel tree-based implementation of the generic estimator proposed in Lee, Chen, Ishwaran (2017), which was designed for handling time-dependent covariates in a fully nonparametric manner. BoXHED is also the first publicly available software implementation for Lee, Chen, Ishwaran (2017). Applying BoXHED to cardiovascular disease onset data from the Framingham Heart Study reveals novel interaction effects among known risk factors, potentially resolving an open question in clinical literature.

Super-resolution estimation of cyclic arrival rates

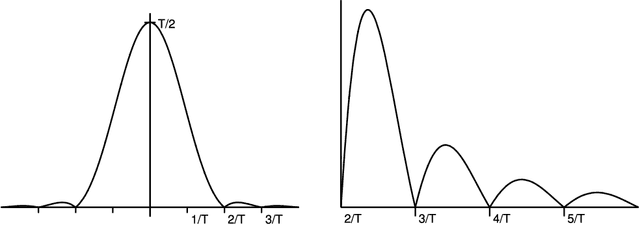
Exploiting the fact that most arrival processes exhibit cyclic behaviour, we propose a simple procedure for estimating the intensity of a nonhomogeneous Poisson process. The estimator is the super-resolution analogue to Shao 2010 and Shao & Lii 2011, which is a sum of $p$ sinusoids where $p$ and the frequency, amplitude, and phase of each wave are not known and need to be estimated. This results in an interpretable yet flexible specification that is suitable for use in modelling as well as in high resolution simulations. Our estimation procedure sits in between classic periodogram methods and atomic/total variation norm thresholding. Through a novel use of window functions in the point process domain, our approach attains super-resolution without semidefinite programming. Under suitable conditions, finite sample guarantees can be derived for our procedure. These resolve some open questions and expand existing results in spectral estimation literature.

Boosting hazard regression with time-varying covariates

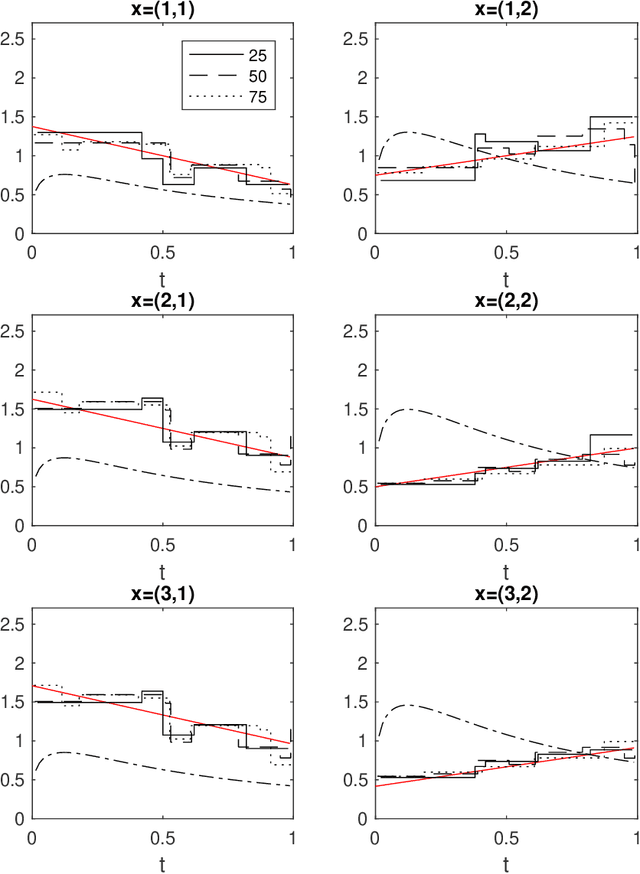
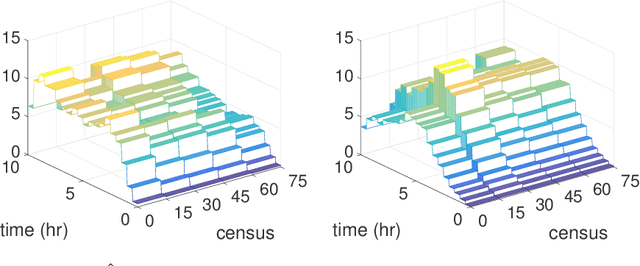
Consider a left-truncated right-censored survival process whose evolution depends on time-varying covariates. Given functional data samples from the process, we propose a practical boosting procedure for estimating its log-intensity function. Our method does not require any separability assumptions like Cox proportional- or Aalen additive-hazards, thus it can flexibly capture time-covariate interactions. The estimator is consistent if the model is correctly specified; alternatively an oracle inequality can be demonstrated for tree-based models. We use the procedure to shed new light on a question from the operations literature concerning the effect of workload on service rates in an emergency department.