Boosting hazard regression with time-varying covariates
Paper and Code
Feb 09, 2018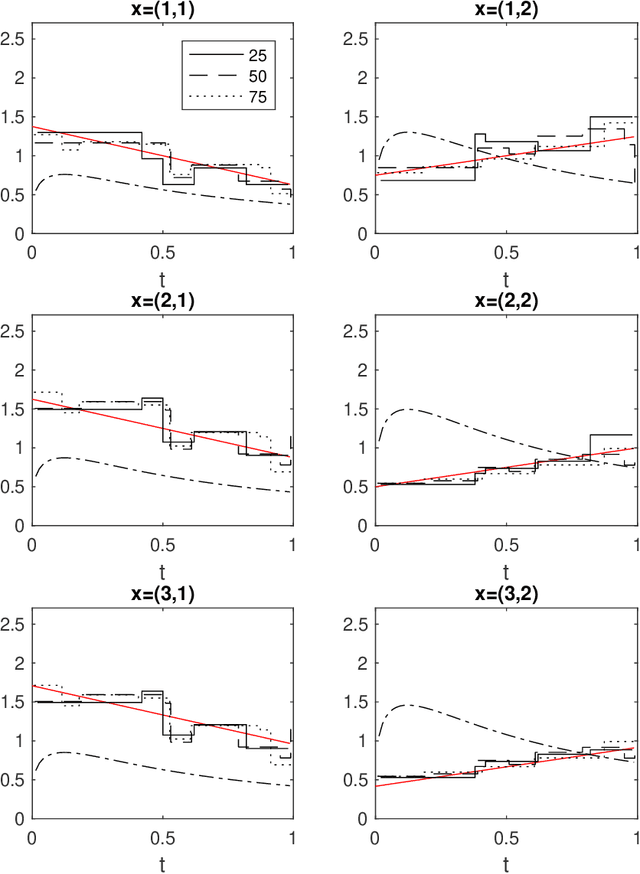

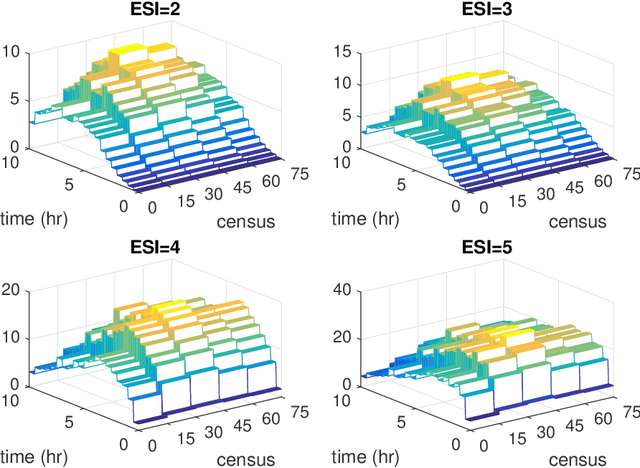
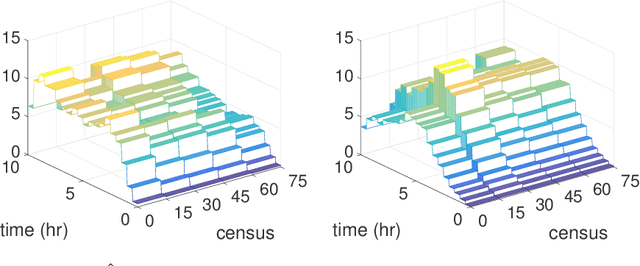
Consider a left-truncated right-censored survival process whose evolution depends on time-varying covariates. Given functional data samples from the process, we propose a practical boosting procedure for estimating its log-intensity function. Our method does not require any separability assumptions like Cox proportional- or Aalen additive-hazards, thus it can flexibly capture time-covariate interactions. The estimator is consistent if the model is correctly specified; alternatively an oracle inequality can be demonstrated for tree-based models. We use the procedure to shed new light on a question from the operations literature concerning the effect of workload on service rates in an emergency department.
* 33 pages, 5 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge