Reducing the Communication Cost of Federated Learning through Multistage Optimization

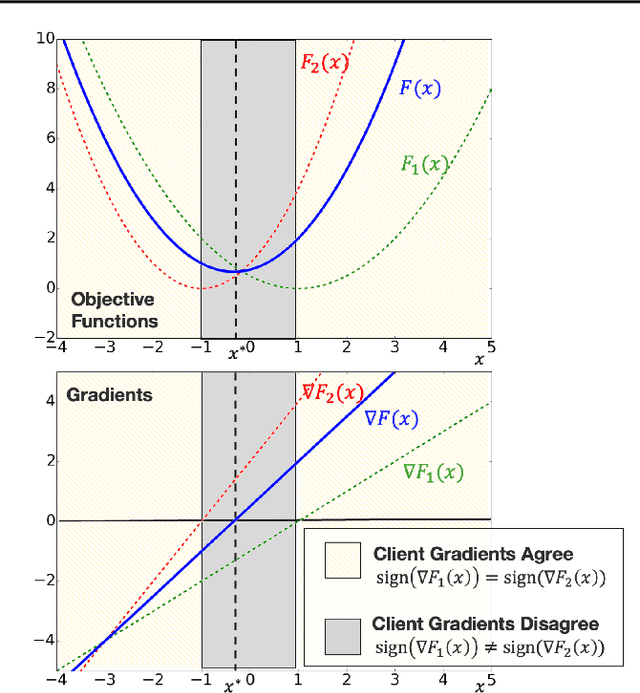
A central question in federated learning (FL) is how to design optimization algorithms that minimize the communication cost of training a model over heterogeneous data distributed across many clients. A popular technique for reducing communication is the use of local steps, where clients take multiple optimization steps over local data before communicating with the server (e.g., FedAvg, SCAFFOLD). This contrasts with centralized methods, where clients take one optimization step per communication round (e.g., Minibatch SGD). A recent lower bound on the communication complexity of first-order methods shows that centralized methods are optimal over highly-heterogeneous data, whereas local methods are optimal over purely homogeneous data [Woodworth et al., 2020]. For intermediate heterogeneity levels, no algorithm is known to match the lower bound. In this paper, we propose a multistage optimization scheme that nearly matches the lower bound across all heterogeneity levels. The idea is to first run a local method up to a heterogeneity-induced error floor; next, we switch to a centralized method for the remaining steps. Our analysis may help explain empirically-successful stepsize decay methods in FL [Charles et al., 2020; Reddi et al., 2020]. We demonstrate the scheme's practical utility in image classification tasks.

Efficient Algorithms for Federated Saddle Point Optimization

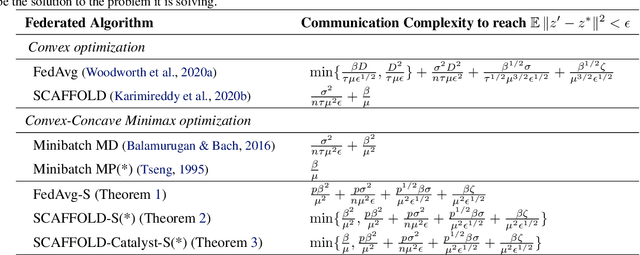
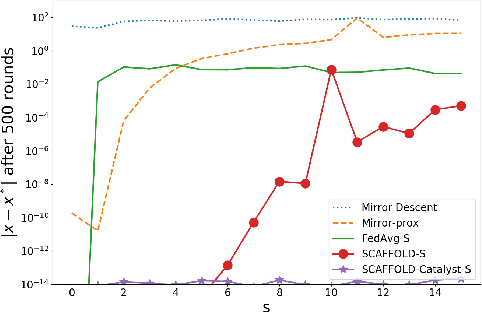
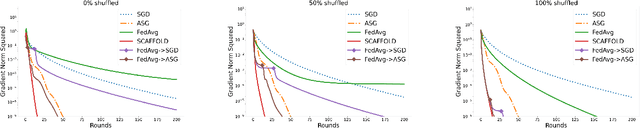
We consider strongly convex-concave minimax problems in the federated setting, where the communication constraint is the main bottleneck. When clients are arbitrarily heterogeneous, a simple Minibatch Mirror-prox achieves the best performance. As the clients become more homogeneous, using multiple local gradient updates at the clients significantly improves upon Minibatch Mirror-prox by communicating less frequently. Our goal is to design an algorithm that can harness the benefit of similarity in the clients while recovering the Minibatch Mirror-prox performance under arbitrary heterogeneity (up to log factors). We give the first federated minimax optimization algorithm that achieves this goal. The main idea is to combine (i) SCAFFOLD (an algorithm that performs variance reduction across clients for convex optimization) to erase the worst-case dependency on heterogeneity and (ii) Catalyst (a framework for acceleration based on modifying the objective) to accelerate convergence without amplifying client drift. We prove that this algorithm achieves our goal, and include experiments to validate the theory.

Attention-based Graph Neural Network for Semi-supervised Learning

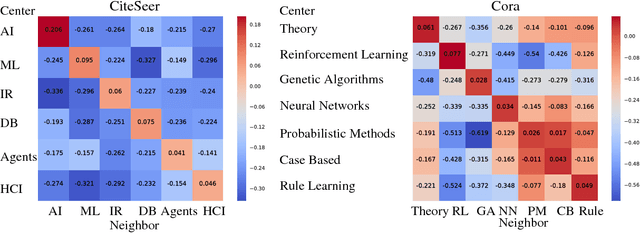
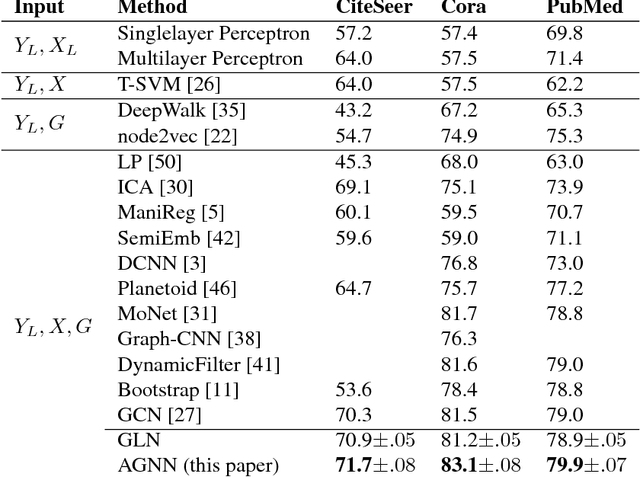
Recently popularized graph neural networks achieve the state-of-the-art accuracy on a number of standard benchmark datasets for graph-based semi-supervised learning, improving significantly over existing approaches. These architectures alternate between a propagation layer that aggregates the hidden states of the local neighborhood and a fully-connected layer. Perhaps surprisingly, we show that a linear model, that removes all the intermediate fully-connected layers, is still able to achieve a performance comparable to the state-of-the-art models. This significantly reduces the number of parameters, which is critical for semi-supervised learning where number of labeled examples are small. This in turn allows a room for designing more innovative propagation layers. Based on this insight, we propose a novel graph neural network that removes all the intermediate fully-connected layers, and replaces the propagation layers with attention mechanisms that respect the structure of the graph. The attention mechanism allows us to learn a dynamic and adaptive local summary of the neighborhood to achieve more accurate predictions. In a number of experiments on benchmark citation networks datasets, we demonstrate that our approach outperforms competing methods. By examining the attention weights among neighbors, we show that our model provides some interesting insights on how neighbors influence each other.

Learning from Comparisons and Choices

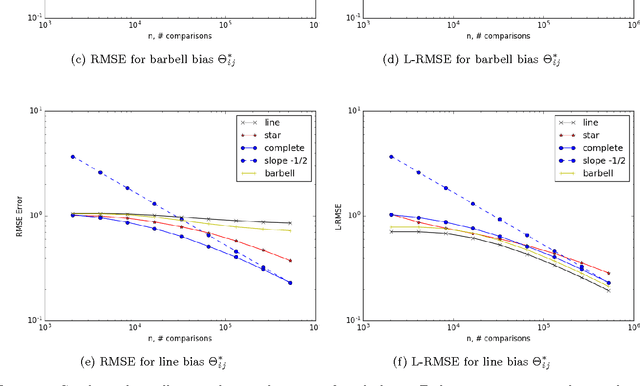
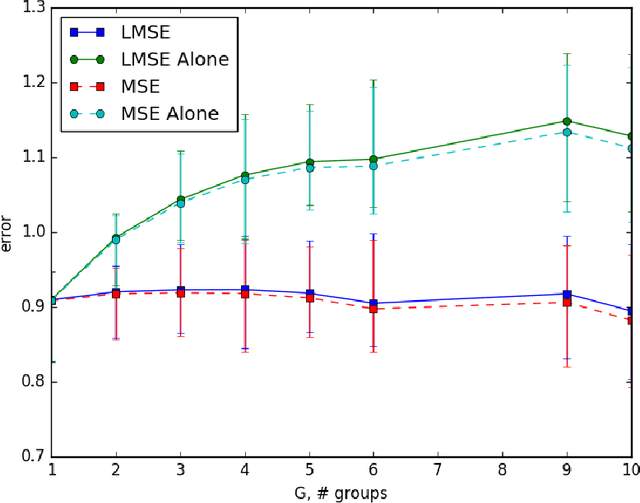
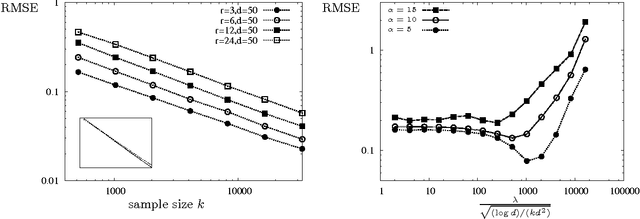
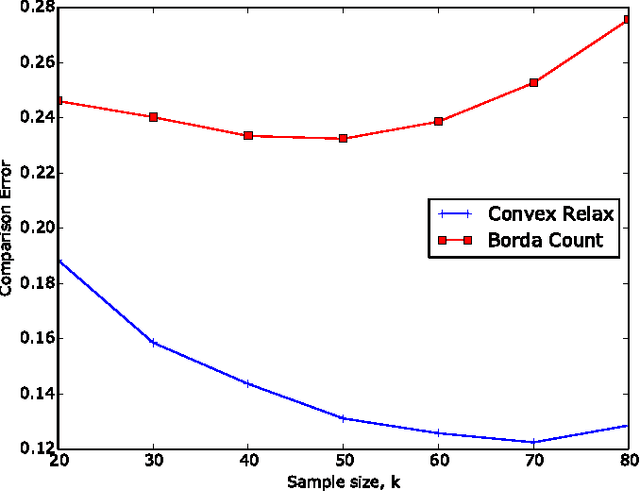
When tracking user-specific online activities, each user's preference is revealed in the form of choices and comparisons. For example, a user's purchase history tracks her choices, i.e. which item was chosen among a subset of offerings. A user's comparisons are observed either explicitly as in movie ratings or implicitly as in viewing times of news articles. Given such individualized ordinal data, we address the problem of collaboratively learning representations of the users and the items. The learned features can be used to predict a user's preference of an unseen item to be used in recommendation systems. This also allows one to compute similarities among users and items to be used for categorization and search. Motivated by the empirical successes of the MultiNomial Logit (MNL) model in marketing and transportation, and also more recent successes in word embedding and crowdsourced image embedding, we pose this problem as learning the MNL model parameters that best explains the data. We propose a convex optimization for learning the MNL model, and show that it is minimax optimal up to a logarithmic factor by comparing its performance to a fundamental lower bound. This characterizes the minimax sample complexity of the problem, and proves that the proposed estimator cannot be improved upon other than by a logarithmic factor. Further, the analysis identifies how the accuracy depends on the topology of sampling via the spectrum of the sampling graph. This provides a guideline for designing surveys when one can choose which items are to be compared. This is accompanies by numerical simulations on synthetic and real datasets confirming our theoretical predictions.

Collaboratively Learning Preferences from Ordinal Data

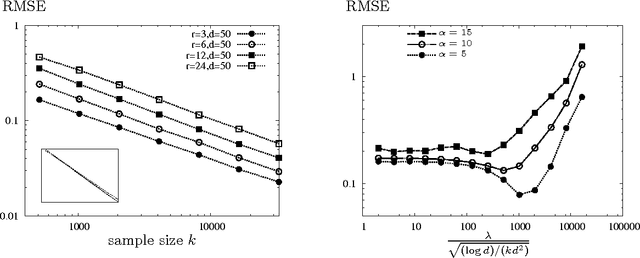
In applications such as recommendation systems and revenue management, it is important to predict preferences on items that have not been seen by a user or predict outcomes of comparisons among those that have never been compared. A popular discrete choice model of multinomial logit model captures the structure of the hidden preferences with a low-rank matrix. In order to predict the preferences, we want to learn the underlying model from noisy observations of the low-rank matrix, collected as revealed preferences in various forms of ordinal data. A natural approach to learn such a model is to solve a convex relaxation of nuclear norm minimization. We present the convex relaxation approach in two contexts of interest: collaborative ranking and bundled choice modeling. In both cases, we show that the convex relaxation is minimax optimal. We prove an upper bound on the resulting error with finite samples, and provide a matching information-theoretic lower bound.