FollowGen: A Scaled Noise Conditional Diffusion Model for Car-Following Trajectory Prediction

Vehicle trajectory prediction is crucial for advancing autonomous driving and advanced driver assistance systems (ADAS). Although deep learning-based approaches - especially those utilizing transformer-based and generative models - have markedly improved prediction accuracy by capturing complex, non-linear patterns in vehicle dynamics and traffic interactions, they frequently overlook detailed car-following behaviors and the inter-vehicle interactions critical for real-world driving applications, particularly in fully autonomous or mixed traffic scenarios. To address the issue, this study introduces a scaled noise conditional diffusion model for car-following trajectory prediction, which integrates detailed inter-vehicular interactions and car-following dynamics into a generative framework, improving both the accuracy and plausibility of predicted trajectories. The model utilizes a novel pipeline to capture historical vehicle dynamics by scaling noise with encoded historical features within the diffusion process. Particularly, it employs a cross-attention-based transformer architecture to model intricate inter-vehicle dependencies, effectively guiding the denoising process and enhancing prediction accuracy. Experimental results on diverse real-world driving scenarios demonstrate the state-of-the-art performance and robustness of the proposed method.

Real-World Data Inspired Interactive Connected Traffic Scenario Generation

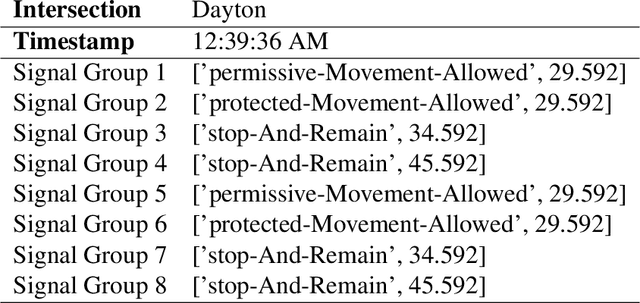
Simulation is a crucial step in ensuring accurate, efficient, and realistic Connected and Autonomous Vehicles (CAVs) testing and validation. As the adoption of CAV accelerates, the integration of real-world data into simulation environments becomes increasingly critical. Among various technologies utilized by CAVs, Vehicle-to-Everything (V2X) communication plays a crucial role in ensuring a seamless transmission of information between CAVs, infrastructure, and other road users. However, most existing studies have focused on developing and testing communication protocols, resource allocation strategies, and data dissemination techniques in V2X. There is a gap where real-world V2X data is integrated into simulations to generate diverse and high-fidelity traffic scenarios. To fulfill this research gap, we leverage real-world Signal Phase and Timing (SPaT) data from Roadside Units (RSUs) to enhance the fidelity of CAV simulations. Moreover, we developed an algorithm that enables Autonomous Vehicles (AVs) to respond dynamically to real-time traffic signal data, simulating realistic V2X communication scenarios. Such high-fidelity simulation environments can generate multimodal data, including trajectory, semantic camera, depth camera, and bird's eye view data for various traffic scenarios. The generated scenarios and data provide invaluable insights into AVs' interactions with traffic infrastructure and other road users. This work aims to bridge the gap between theoretical research and practical deployment of CAVs, facilitating the development of smarter and safer transportation systems.

V2X-VLM: End-to-End V2X Cooperative Autonomous Driving Through Large Vision-Language Models

Advancements in autonomous driving have increasingly focused on end-to-end (E2E) systems that manage the full spectrum of driving tasks, from environmental perception to vehicle navigation and control. This paper introduces V2X-VLM, an innovative E2E vehicle-infrastructure cooperative autonomous driving (VICAD) framework with large vision-language models (VLMs). V2X-VLM is designed to enhance situational awareness, decision-making, and ultimate trajectory planning by integrating data from vehicle-mounted cameras, infrastructure sensors, and textual information. The strength of the comprehensive multimodel data fusion of the VLM enables precise and safe E2E trajectory planning in complex and dynamic driving scenarios. Validation on the DAIR-V2X dataset demonstrates that V2X-VLM outperforms existing state-of-the-art methods in cooperative autonomous driving.

Fast Neighborhood Graph Search using Cartesian Concatenation

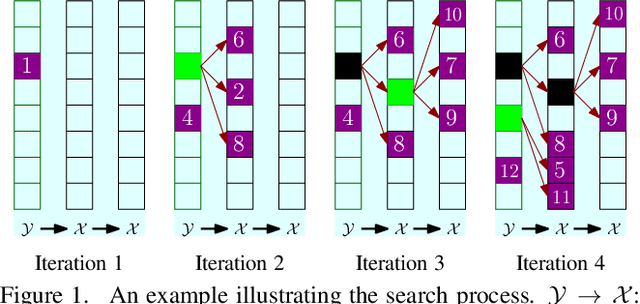
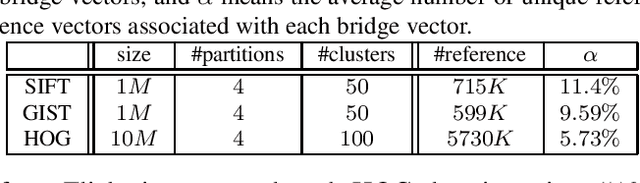
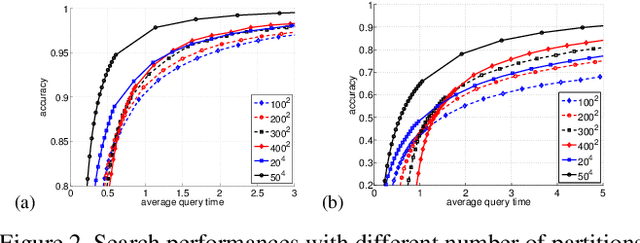
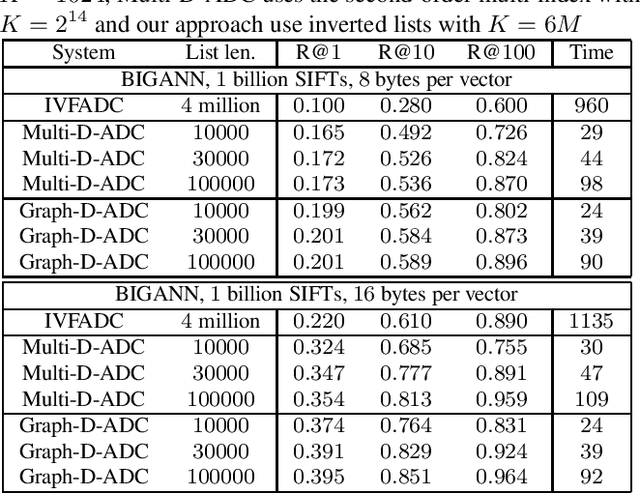
In this paper, we propose a new data structure for approximate nearest neighbor search. This structure augments the neighborhood graph with a bridge graph. We propose to exploit Cartesian concatenation to produce a large set of vectors, called bridge vectors, from several small sets of subvectors. Each bridge vector is connected with a few reference vectors near to it, forming a bridge graph. Our approach finds nearest neighbors by simultaneously traversing the neighborhood graph and the bridge graph in the best-first strategy. The success of our approach stems from two factors: the exact nearest neighbor search over a large number of bridge vectors can be done quickly, and the reference vectors connected to a bridge (reference) vector near the query are also likely to be near the query. Experimental results on searching over large scale datasets (SIFT, GIST and HOG) show that our approach outperforms state-of-the-art ANN search algorithms in terms of efficiency and accuracy. The combination of our approach with the IVFADC system also shows superior performance over the BIGANN dataset of $1$ billion SIFT features compared with the best previously published result.

Scalable $k$-NN graph construction

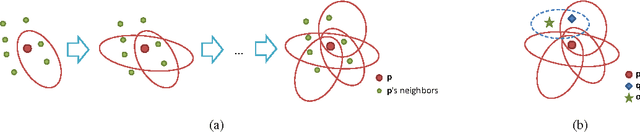
The $k$-NN graph has played a central role in increasingly popular data-driven techniques for various learning and vision tasks; yet, finding an efficient and effective way to construct $k$-NN graphs remains a challenge, especially for large-scale high-dimensional data. In this paper, we propose a new approach to construct approximate $k$-NN graphs with emphasis in: efficiency and accuracy. We hierarchically and randomly divide the data points into subsets and build an exact neighborhood graph over each subset, achieving a base approximate neighborhood graph; we then repeat this process for several times to generate multiple neighborhood graphs, which are combined to yield a more accurate approximate neighborhood graph. Furthermore, we propose a neighborhood propagation scheme to further enhance the accuracy. We show both theoretical and empirical accuracy and efficiency of our approach to $k$-NN graph construction and demonstrate significant speed-up in dealing with large scale visual data.