Fast Neighborhood Graph Search using Cartesian Concatenation
Paper and Code
Dec 11, 2013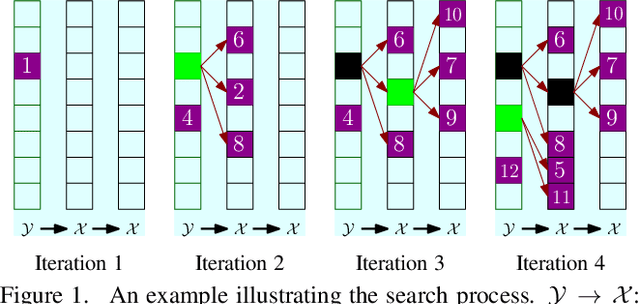
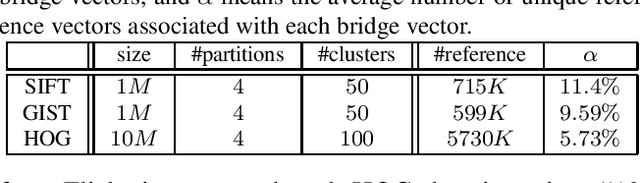
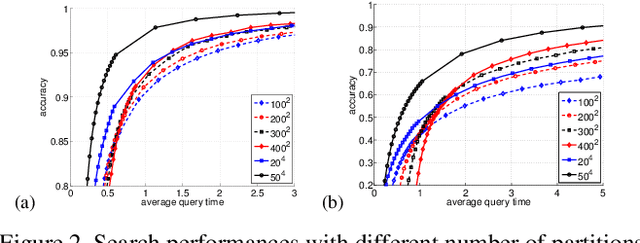
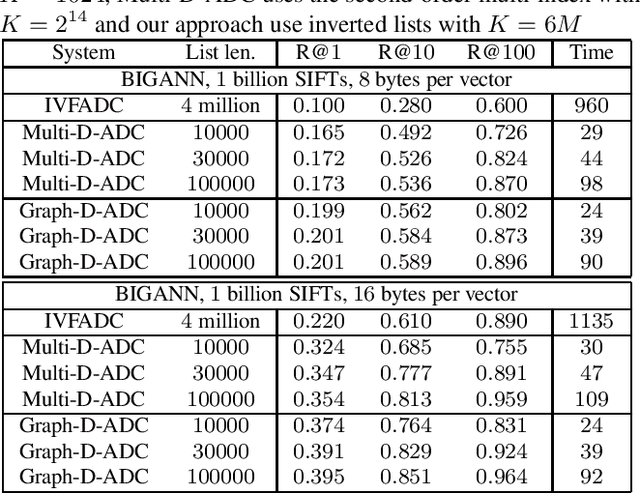
In this paper, we propose a new data structure for approximate nearest neighbor search. This structure augments the neighborhood graph with a bridge graph. We propose to exploit Cartesian concatenation to produce a large set of vectors, called bridge vectors, from several small sets of subvectors. Each bridge vector is connected with a few reference vectors near to it, forming a bridge graph. Our approach finds nearest neighbors by simultaneously traversing the neighborhood graph and the bridge graph in the best-first strategy. The success of our approach stems from two factors: the exact nearest neighbor search over a large number of bridge vectors can be done quickly, and the reference vectors connected to a bridge (reference) vector near the query are also likely to be near the query. Experimental results on searching over large scale datasets (SIFT, GIST and HOG) show that our approach outperforms state-of-the-art ANN search algorithms in terms of efficiency and accuracy. The combination of our approach with the IVFADC system also shows superior performance over the BIGANN dataset of $1$ billion SIFT features compared with the best previously published result.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge