Enhance Hyperbolic Representation Learning via Second-order Pooling

Hyperbolic representation learning is well known for its ability to capture hierarchical information. However, the distance between samples from different levels of hierarchical classes can be required large. We reveal that the hyperbolic discriminant objective forces the backbone to capture this hierarchical information, which may inevitably increase the Lipschitz constant of the backbone. This can hinder the full utilization of the backbone's generalization ability. To address this issue, we introduce second-order pooling into hyperbolic representation learning, as it naturally increases the distance between samples without compromising the generalization ability of the input features. In this way, the Lipschitz constant of the backbone does not necessarily need to be large. However, current off-the-shelf low-dimensional bilinear pooling methods cannot be directly employed in hyperbolic representation learning because they inevitably reduce the distance expansion capability. To solve this problem, we propose a kernel approximation regularization, which enables the low-dimensional bilinear features to approximate the kernel function well in low-dimensional space. Finally, we conduct extensive experiments on graph-structured datasets to demonstrate the effectiveness of the proposed method.

Reinforcement Learning for Solving Stochastic Vehicle Routing Problem with Time Windows

This paper introduces a reinforcement learning approach to optimize the Stochastic Vehicle Routing Problem with Time Windows (SVRP), focusing on reducing travel costs in goods delivery. We develop a novel SVRP formulation that accounts for uncertain travel costs and demands, alongside specific customer time windows. An attention-based neural network trained through reinforcement learning is employed to minimize routing costs. Our approach addresses a gap in SVRP research, which traditionally relies on heuristic methods, by leveraging machine learning. The model outperforms the Ant-Colony Optimization algorithm, achieving a 1.73% reduction in travel costs. It uniquely integrates external information, demonstrating robustness in diverse environments, making it a valuable benchmark for future SVRP studies and industry application.

Reinforcement Learning for Solving Stochastic Vehicle Routing Problem

This study addresses a gap in the utilization of Reinforcement Learning (RL) and Machine Learning (ML) techniques in solving the Stochastic Vehicle Routing Problem (SVRP) that involves the challenging task of optimizing vehicle routes under uncertain conditions. We propose a novel end-to-end framework that comprehensively addresses the key sources of stochasticity in SVRP and utilizes an RL agent with a simple yet effective architecture and a tailored training method. Through comparative analysis, our proposed model demonstrates superior performance compared to a widely adopted state-of-the-art metaheuristic, achieving a significant 3.43% reduction in travel costs. Furthermore, the model exhibits robustness across diverse SVRP settings, highlighting its adaptability and ability to learn optimal routing strategies in varying environments. The publicly available implementation of our framework serves as a valuable resource for future research endeavors aimed at advancing RL-based solutions for SVRP.

Regularization of the policy updates for stabilizing Mean Field Games

This work studies non-cooperative Multi-Agent Reinforcement Learning (MARL) where multiple agents interact in the same environment and whose goal is to maximize the individual returns. Challenges arise when scaling up the number of agents due to the resultant non-stationarity that the many agents introduce. In order to address this issue, Mean Field Games (MFG) rely on the symmetry and homogeneity assumptions to approximate games with very large populations. Recently, deep Reinforcement Learning has been used to scale MFG to games with larger number of states. Current methods rely on smoothing techniques such as averaging the q-values or the updates on the mean-field distribution. This work presents a different approach to stabilize the learning based on proximal updates on the mean-field policy. We name our algorithm Mean Field Proximal Policy Optimization (MF-PPO), and we empirically show the effectiveness of our method in the OpenSpiel framework.

Learning to generalize Dispatching rules on the Job Shop Scheduling

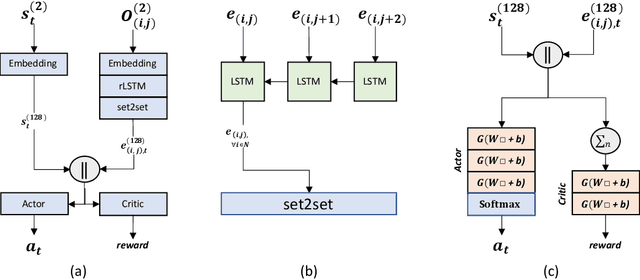
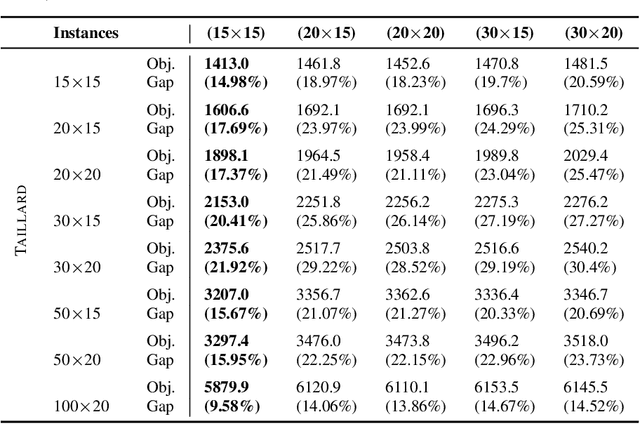
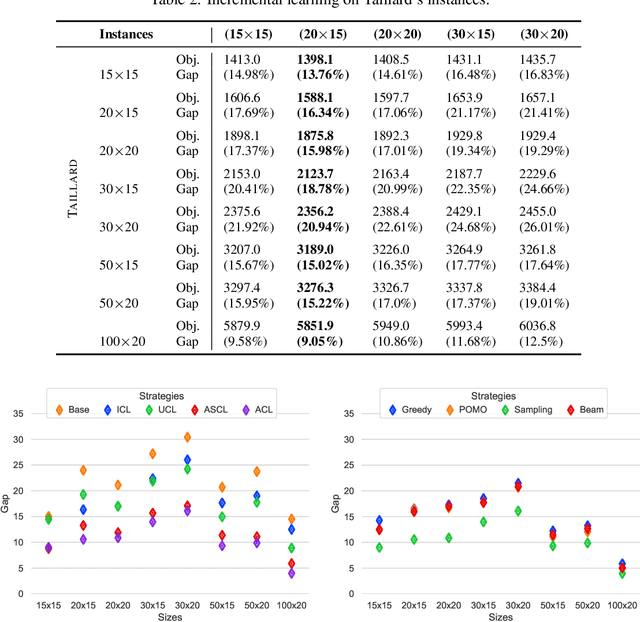
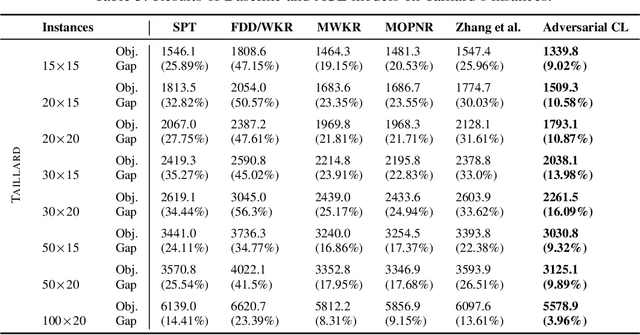
This paper introduces a Reinforcement Learning approach to better generalize heuristic dispatching rules on the Job-shop Scheduling Problem (JSP). Current models on the JSP do not focus on generalization, although, as we show in this work, this is key to learning better heuristics on the problem. A well-known technique to improve generalization is to learn on increasingly complex instances using Curriculum Learning (CL). However, as many works in the literature indicate, this technique might suffer from catastrophic forgetting when transferring the learned skills between different problem sizes. To address this issue, we introduce a novel Adversarial Curriculum Learning (ACL) strategy, which dynamically adjusts the difficulty level during the learning process to revisit the worst-performing instances. This work also presents a deep learning model to solve the JSP, which is equivariant w.r.t. the job definition and size-agnostic. Conducted experiments on Taillard's and Demirkol's instances show that the presented approach significantly improves the current state-of-the-art models on the JSP. It reduces the average optimality gap from 19.35\% to 10.46\% on Taillard's instances and from 38.43\% to 18.85\% on Demirkol's instances. Our implementation is available online.

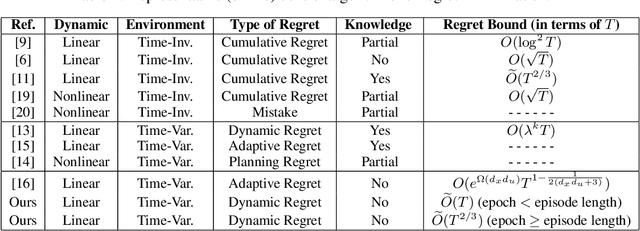
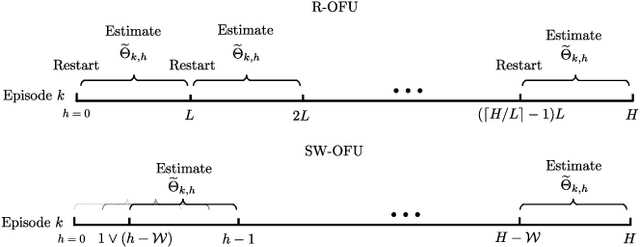
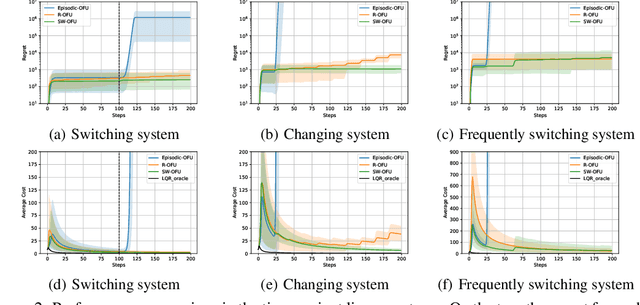
Learning to Control under Time-Varying Environment

This paper investigates the problem of regret minimization in linear time-varying (LTV) dynamical systems. Due to the simultaneous presence of uncertainty and non-stationarity, designing online control algorithms for unknown LTV systems remains a challenging task. At a cost of NP-hard offline planning, prior works have introduced online convex optimization algorithms, although they suffer from nonparametric rate of regret. In this paper, we propose the first computationally tractable online algorithm with regret guarantees that avoids offline planning over the state linear feedback policies. Our algorithm is based on the optimism in the face of uncertainty (OFU) principle in which we optimistically select the best model in a high confidence region. Our algorithm is then more explorative when compared to previous approaches. To overcome non-stationarity, we propose either a restarting strategy (R-OFU) or a sliding window (SW-OFU) strategy. With proper configuration, our algorithm is attains sublinear regret $O(T^{2/3})$. These algorithms utilize data from the current phase for tracking variations on the system dynamics. We corroborate our theoretical findings with numerical experiments, which highlight the effectiveness of our methods. To the best of our knowledge, our study establishes the first model-based online algorithm with regret guarantees under LTV dynamical systems.

Constrained Combinatorial Optimization with Reinforcement Learning

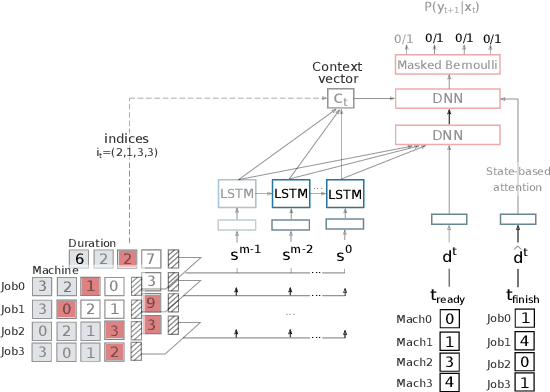
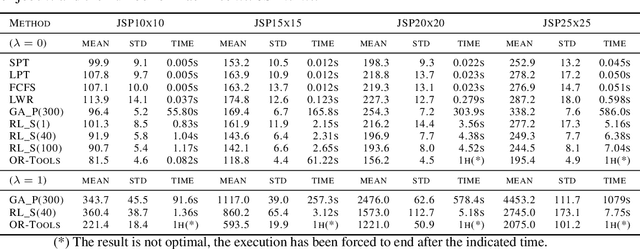
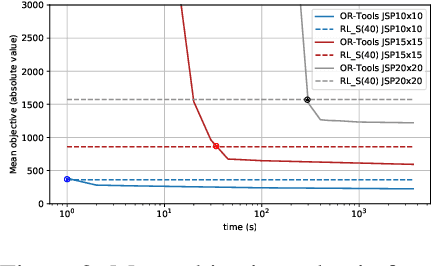
This paper presents a framework to tackle constrained combinatorial optimization problems using deep Reinforcement Learning (RL). To this end, we extend the Neural Combinatorial Optimization (NCO) theory in order to deal with constraints in its formulation. Notably, we propose defining constrained combinatorial problems as fully observable Constrained Markov Decision Processes (CMDP). In that context, the solution is iteratively constructed based on interactions with the environment. The model, in addition to the reward signal, relies on penalty signals generated from constraint dissatisfaction to infer a policy that acts as a heuristic algorithm. Moreover, having access to the complete state representation during the optimization process allows us to rely on memory-less architectures, enhancing the results obtained in previous sequence-to-sequence approaches. Conducted experiments on the constrained Job Shop and Resource Allocation problems prove the superiority of the proposal for computing rapid solutions when compared to classical heuristic, metaheuristic, and Constraint Programming (CP) solvers.