Constrained Combinatorial Optimization with Reinforcement Learning
Paper and Code
Jun 22, 2020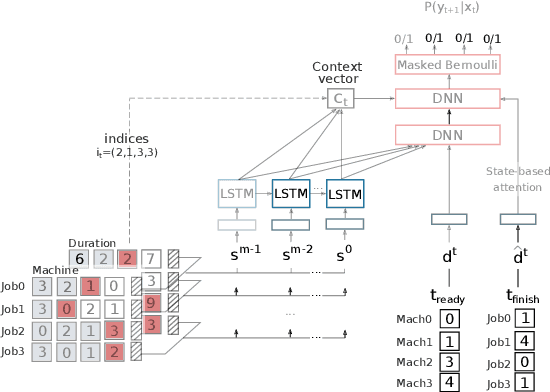
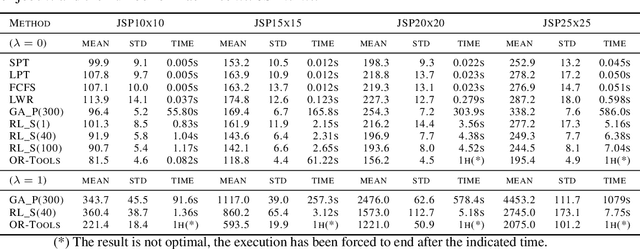

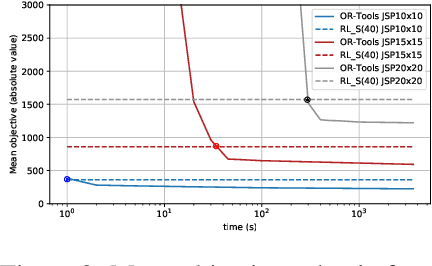
This paper presents a framework to tackle constrained combinatorial optimization problems using deep Reinforcement Learning (RL). To this end, we extend the Neural Combinatorial Optimization (NCO) theory in order to deal with constraints in its formulation. Notably, we propose defining constrained combinatorial problems as fully observable Constrained Markov Decision Processes (CMDP). In that context, the solution is iteratively constructed based on interactions with the environment. The model, in addition to the reward signal, relies on penalty signals generated from constraint dissatisfaction to infer a policy that acts as a heuristic algorithm. Moreover, having access to the complete state representation during the optimization process allows us to rely on memory-less architectures, enhancing the results obtained in previous sequence-to-sequence approaches. Conducted experiments on the constrained Job Shop and Resource Allocation problems prove the superiority of the proposal for computing rapid solutions when compared to classical heuristic, metaheuristic, and Constraint Programming (CP) solvers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge