Governing equation discovery of a complex system from snapshots

Complex systems in physics, chemistry, and biology that evolve over time with inherent randomness are typically described by stochastic differential equations (SDEs). A fundamental challenge in science and engineering is to determine the governing equations of a complex system from snapshot data. Traditional equation discovery methods often rely on stringent assumptions, such as the availability of the trajectory information or time-series data, and the presumption that the underlying system is deterministic. In this work, we introduce a data-driven, simulation-free framework, called Sparse Identification of Differential Equations from Snapshots (SpIDES), that discovers the governing equations of a complex system from snapshots by utilizing the advanced machine learning techniques to perform three essential steps: probability flow reconstruction, probability density estimation, and Bayesian sparse identification. We validate the effectiveness and robustness of SpIDES by successfully identifying the governing equation of an over-damped Langevin system confined within two potential wells. By extracting interpretable drift and diffusion terms from the SDEs, our framework provides deeper insights into system dynamics, enhances predictive accuracy, and facilitates more effective strategies for managing and simulating stochastic systems.

Learning Hamiltonian neural Koopman operator and simultaneously sustaining and discovering conservation law

Accurately finding and predicting dynamics based on the observational data with noise perturbations is of paramount significance but still a major challenge presently. Here, for the Hamiltonian mechanics, we propose the Hamiltonian Neural Koopman Operator (HNKO), integrating the knowledge of mathematical physics in learning the Koopman operator, and making it automatically sustain and even discover the conservation laws. We demonstrate the outperformance of the HNKO and its extension using a number of representative physical systems even with hundreds or thousands of freedoms. Our results suggest that feeding the prior knowledge of the underlying system and the mathematical theory appropriately to the learning framework can reinforce the capability of machine learning in solving physical problems.

From Fourier to Neural ODEs: Flow Matching for Modeling Complex Systems

Modeling complex systems using standard neural ordinary differential equations (NODEs) often faces some essential challenges, including high computational costs and susceptibility to local optima. To address these challenges, we propose a simulation-free framework, called Fourier NODEs (FNODEs), that effectively trains NODEs by directly matching the target vector field based on Fourier analysis. Specifically, we employ the Fourier analysis to estimate temporal and potential high-order spatial gradients from noisy observational data. We then incorporate the estimated spatial gradients as additional inputs to a neural network. Furthermore, we utilize the estimated temporal gradient as the optimization objective for the output of the neural network. Later, the trained neural network generates more data points through an ODE solver without participating in the computational graph, facilitating more accurate estimations of gradients based on Fourier analysis. These two steps form a positive feedback loop, enabling accurate dynamics modeling in our framework. Consequently, our approach outperforms state-of-the-art methods in terms of training time, dynamics prediction, and robustness. Finally, we demonstrate the superior performance of our framework using a number of representative complex systems.

Switched Flow Matching: Eliminating Singularities via Switching ODEs

Continuous-time generative models, such as Flow Matching (FM), construct probability paths to transport between one distribution and another through the simulation-free learning of the neural ordinary differential equations (ODEs). During inference, however, the learned model often requires multiple neural network evaluations to accurately integrate the flow, resulting in a slow sampling speed. We attribute the reason to the inherent (joint) heterogeneity of source and/or target distributions, namely the singularity problem, which poses challenges for training the neural ODEs effectively. To address this issue, we propose a more general framework, termed Switched FM (SFM), that eliminates singularities via switching ODEs, as opposed to using a uniform ODE in FM. Importantly, we theoretically show that FM cannot transport between two simple distributions due to the existence and uniqueness of initial value problems of ODEs, while these limitations can be well tackled by SFM. From an orthogonal perspective, our framework can seamlessly integrate with the existing advanced techniques, such as minibatch optimal transport, to further enhance the straightness of the flow, yielding a more efficient sampling process with reduced costs. We demonstrate the effectiveness of the newly proposed SFM through several numerical examples.

Let's Rectify Step by Step: Improving Aspect-based Sentiment Analysis with Diffusion Models

Aspect-Based Sentiment Analysis (ABSA) stands as a crucial task in predicting the sentiment polarity associated with identified aspects within text. However, a notable challenge in ABSA lies in precisely determining the aspects' boundaries (start and end indices), especially for long ones, due to users' colloquial expressions. We propose DiffusionABSA, a novel diffusion model tailored for ABSA, which extracts the aspects progressively step by step. Particularly, DiffusionABSA gradually adds noise to the aspect terms in the training process, subsequently learning a denoising process that progressively restores these terms in a reverse manner. To estimate the boundaries, we design a denoising neural network enhanced by a syntax-aware temporal attention mechanism to chronologically capture the interplay between aspects and surrounding text. Empirical evaluations conducted on eight benchmark datasets underscore the compelling advantages offered by DiffusionABSA when compared against robust baseline models. Our code is publicly available at https://github.com/Qlb6x/DiffusionABSA.

A Confidence-based Partial Label Learning Model for Crowd-Annotated Named Entity Recognition

Existing models for named entity recognition (NER) are mainly based on large-scale labeled datasets, which always obtain using crowdsourcing. However, it is hard to obtain a unified and correct label via majority voting from multiple annotators for NER due to the large labeling space and complexity of this task. To address this problem, we aim to utilize the original multi-annotator labels directly. Particularly, we propose a Confidence-based Partial Label Learning (CPLL) method to integrate the prior confidence (given by annotators) and posterior confidences (learned by models) for crowd-annotated NER. This model learns a token- and content-dependent confidence via an Expectation-Maximization (EM) algorithm by minimizing empirical risk. The true posterior estimator and confidence estimator perform iteratively to update the true posterior and confidence respectively. We conduct extensive experimental results on both real-world and synthetic datasets, which show that our model can improve performance effectively compared with strong baselines.

Neural Delay Differential Equations: System Reconstruction and Image Classification

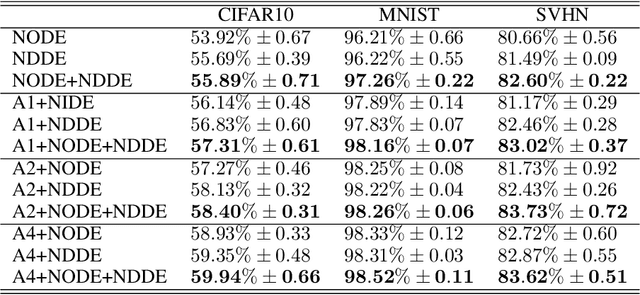
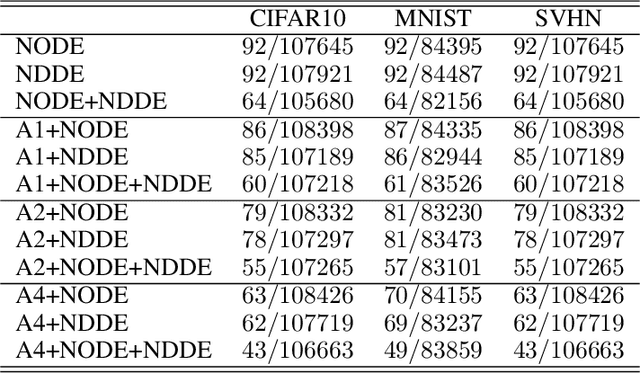
Neural Ordinary Differential Equations (NODEs), a framework of continuous-depth neural networks, have been widely applied, showing exceptional efficacy in coping with representative datasets. Recently, an augmented framework has been developed to overcome some limitations that emerged in the application of the original framework. In this paper, we propose a new class of continuous-depth neural networks with delay, named Neural Delay Differential Equations (NDDEs). To compute the corresponding gradients, we use the adjoint sensitivity method to obtain the delayed dynamics of the adjoint. Differential equations with delays are typically seen as dynamical systems of infinite dimension that possess more fruitful dynamics. Compared to NODEs, NDDEs have a stronger capacity of nonlinear representations. We use several illustrative examples to demonstrate this outstanding capacity. Firstly, we successfully model the delayed dynamics where the trajectories in the lower-dimensional phase space could be mutually intersected and even chaotic in a model-free or model-based manner. Traditional NODEs, without any argumentation, are not directly applicable for such modeling. Secondly, we achieve lower loss and higher accuracy not only for the data produced synthetically by complex models but also for the CIFAR10, a well-known image dataset. Our results on the NDDEs demonstrate that appropriately articulating the elements of dynamical systems into the network design is truly beneficial in promoting network performance.

Neural Piecewise-Constant Delay Differential Equations

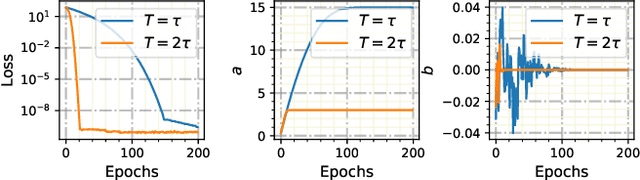
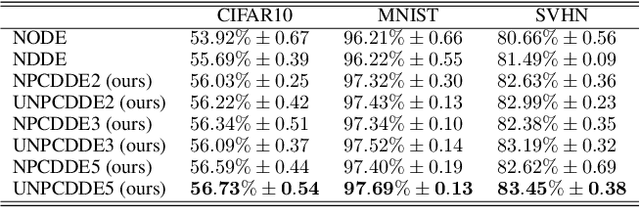
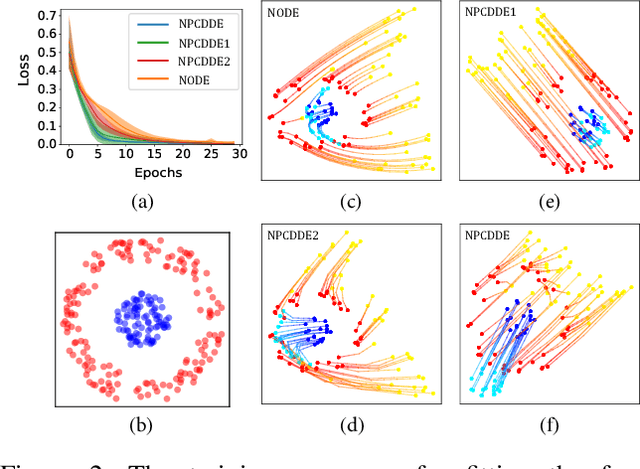
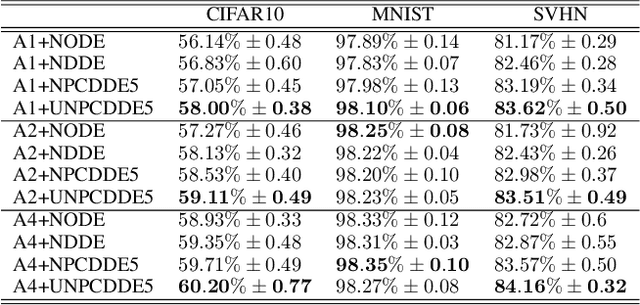
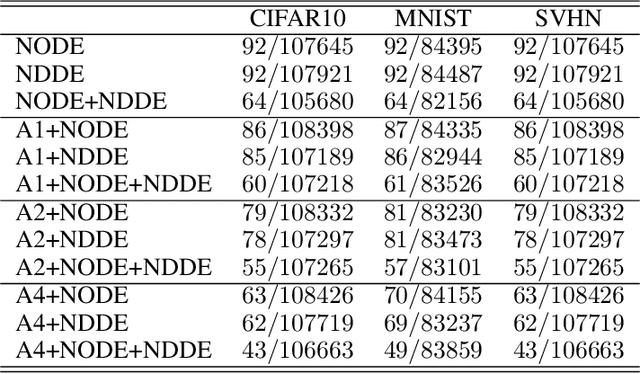
Continuous-depth neural networks, such as the Neural Ordinary Differential Equations (ODEs), have aroused a great deal of interest from the communities of machine learning and data science in recent years, which bridge the connection between deep neural networks and dynamical systems. In this article, we introduce a new sort of continuous-depth neural network, called the Neural Piecewise-Constant Delay Differential Equations (PCDDEs). Here, unlike the recently proposed framework of the Neural Delay Differential Equations (DDEs), we transform the single delay into the piecewise-constant delay(s). The Neural PCDDEs with such a transformation, on one hand, inherit the strength of universal approximating capability in Neural DDEs. On the other hand, the Neural PCDDEs, leveraging the contributions of the information from the multiple previous time steps, further promote the modeling capability without augmenting the network dimension. With such a promotion, we show that the Neural PCDDEs do outperform the several existing continuous-depth neural frameworks on the one-dimensional piecewise-constant delay population dynamics and real-world datasets, including MNIST, CIFAR10, and SVHN.

Neural Delay Differential Equations

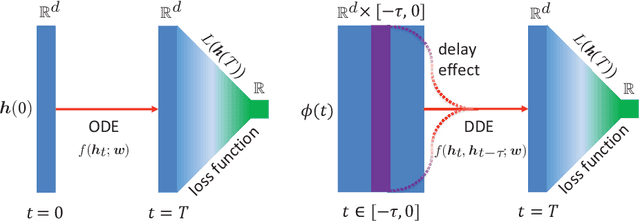
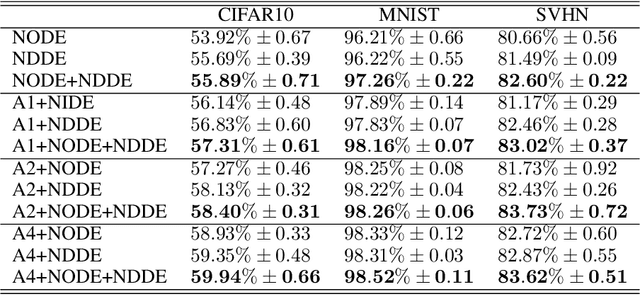
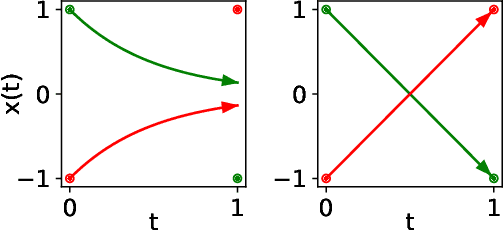
Neural Ordinary Differential Equations (NODEs), a framework of continuous-depth neural networks, have been widely applied, showing exceptional efficacy in coping with some representative datasets. Recently, an augmented framework has been successfully developed for conquering some limitations emergent in application of the original framework. Here we propose a new class of continuous-depth neural networks with delay, named as Neural Delay Differential Equations (NDDEs), and, for computing the corresponding gradients, we use the adjoint sensitivity method to obtain the delayed dynamics of the adjoint. Since the differential equations with delays are usually seen as dynamical systems of infinite dimension possessing more fruitful dynamics, the NDDEs, compared to the NODEs, own a stronger capacity of nonlinear representations. Indeed, we analytically validate that the NDDEs are of universal approximators, and further articulate an extension of the NDDEs, where the initial function of the NDDEs is supposed to satisfy ODEs. More importantly, we use several illustrative examples to demonstrate the outstanding capacities of the NDDEs and the NDDEs with ODEs' initial value. Specifically, (1) we successfully model the delayed dynamics where the trajectories in the lower-dimensional phase space could be mutually intersected, while the traditional NODEs without any argumentation are not directly applicable for such modeling, and (2) we achieve lower loss and higher accuracy not only for the data produced synthetically by complex models but also for the real-world image datasets, i.e., CIFAR10, MNIST, and SVHN. Our results on the NDDEs reveal that appropriately articulating the elements of dynamical systems into the network design is truly beneficial to promoting the network performance.