Symbolic Neural Ordinary Differential Equations

Differential equations are widely used to describe complex dynamical systems with evolving parameters in nature and engineering. Effectively learning a family of maps from the parameter function to the system dynamics is of great significance. In this study, we propose a novel learning framework of symbolic continuous-depth neural networks, termed Symbolic Neural Ordinary Differential Equations (SNODEs), to effectively and accurately learn the underlying dynamics of complex systems. Specifically, our learning framework comprises three stages: initially, pre-training a predefined symbolic neural network via a gradient flow matching strategy; subsequently, fine-tuning this network using Neural ODEs; and finally, constructing a general neural network to capture residuals. In this process, we apply the SNODEs framework to partial differential equation systems through Fourier analysis, achieving resolution-invariant modeling. Moreover, this framework integrates the strengths of symbolism and connectionism, boasting a universal approximation theorem while significantly enhancing interpretability and extrapolation capabilities relative to state-of-the-art baseline methods. We demonstrate this through experiments on several representative complex systems. Therefore, our framework can be further applied to a wide range of scientific problems, such as system bifurcation and control, reconstruction and forecasting, as well as the discovery of new equations.

From Fourier to Neural ODEs: Flow Matching for Modeling Complex Systems

Modeling complex systems using standard neural ordinary differential equations (NODEs) often faces some essential challenges, including high computational costs and susceptibility to local optima. To address these challenges, we propose a simulation-free framework, called Fourier NODEs (FNODEs), that effectively trains NODEs by directly matching the target vector field based on Fourier analysis. Specifically, we employ the Fourier analysis to estimate temporal and potential high-order spatial gradients from noisy observational data. We then incorporate the estimated spatial gradients as additional inputs to a neural network. Furthermore, we utilize the estimated temporal gradient as the optimization objective for the output of the neural network. Later, the trained neural network generates more data points through an ODE solver without participating in the computational graph, facilitating more accurate estimations of gradients based on Fourier analysis. These two steps form a positive feedback loop, enabling accurate dynamics modeling in our framework. Consequently, our approach outperforms state-of-the-art methods in terms of training time, dynamics prediction, and robustness. Finally, we demonstrate the superior performance of our framework using a number of representative complex systems.

CIM-PPO:Proximal Policy Optimization with Liu-Correntropy Induced Metric

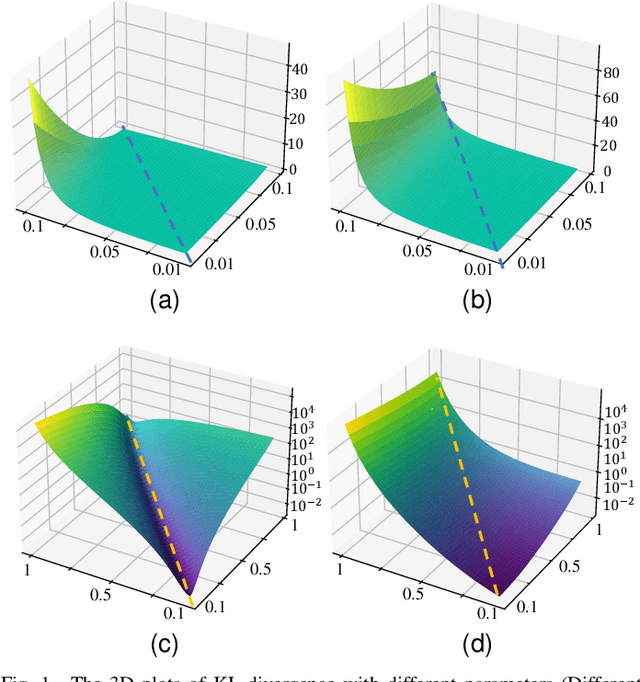
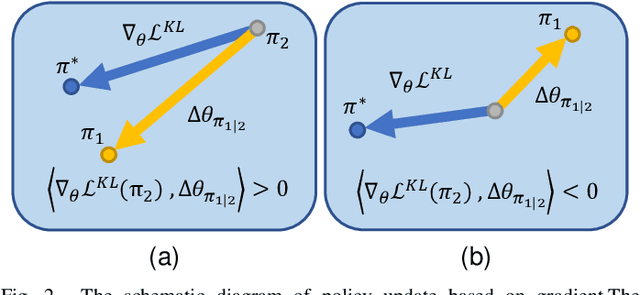
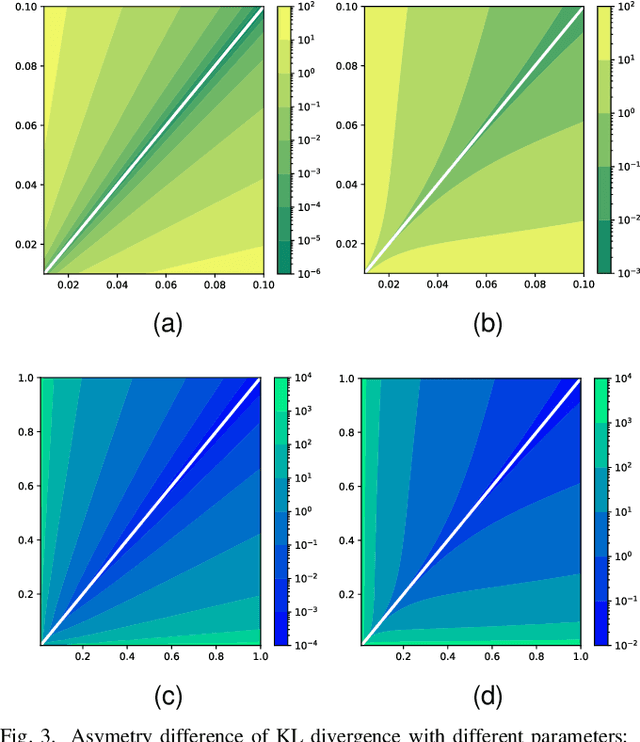
As an algorithm based on deep reinforcement learning, Proximal Policy Optimization (PPO) performs well in many complex tasks and has become one of the most popular RL algorithms in recent years. According to the mechanism of penalty in surrogate objective, PPO can be divided into PPO with KL Divergence (KL-PPO) and PPO with Clip function(Clip-PPO). Clip-PPO is widely used in a variety of practical scenarios and has attracted the attention of many researchers. Therefore, many variations have also been created, making the algorithm better and better. However, as a more theoretical algorithm, KL-PPO was neglected because its performance was not as good as CliP-PPO. In this article, we analyze the asymmetry effect of KL divergence on PPO's objective function , and give the inequality that can indicate when the asymmetry will affect the efficiency of KL-PPO. Proposed PPO with Correntropy Induced Metric algorithm(CIM-PPO) that use the theory of correntropy(a symmetry metric method that was widely used in M-estimation to evaluate two distributions' difference)and applied it in PPO. Then, we designed experiments based on OpenAIgym to test the effectiveness of the new algorithm and compare it with KL-PPO and CliP-PPO.