MR Optimized Reconstruction of Simultaneous Multi-Slice Imaging Using Diffusion Model

Diffusion model has been successfully applied to MRI reconstruction, including single and multi-coil acquisition of MRI data. Simultaneous multi-slice imaging (SMS), as a method for accelerating MR acquisition, can significantly reduce scanning time, but further optimization of reconstruction results is still possible. In order to optimize the reconstruction of SMS, we proposed a method to use diffusion model based on slice-GRAPPA and SPIRiT method. approach: Specifically, our method characterizes the prior distribution of SMS data by score matching and characterizes the k-space redundant prior between coils and slices based on self-consistency. With the utilization of diffusion model, we achieved better reconstruction results.The application of diffusion model can further reduce the scanning time of MRI without compromising image quality, making it more advantageous for clinical application

LINEAR: Learning Implicit Neural Representation With Explicit Physical Priors for Accelerated Quantitative T1rho Mapping

Quantitative T1rho parameter mapping has shown promise in clinical and research studies. However, it suffers from long scan times. Deep learning-based techniques have been successfully applied in accelerated quantitative MR parameter mapping. However, most methods require fully-sampled training dataset, which is impractical in the clinic. In this study, a novel subject-specific unsupervised method based on the implicit neural representation is proposed to reconstruct images from highly undersampled k-space data and estimate parameter maps from reconstructions, which only takes spatiotemporal coordinates as the input. Specifically, the proposed method learned a implicit neural representation of the MR images driven by two explicit priors of images (or k-space data), including the low-rankness of Hankel matrix, and the self-consistency of k-space data. The ablation experiments show that the proposed method can characterize the physical priors of MR images well. Moreover,experimental results of retrospective and prospective data show that the proposed method outperforms the state-of-the-art methods in terms of supressing artifacts and achieving the lowest error.

Physics-Informed DeepMRI: Bridging the Gap from Heat Diffusion to k-Space Interpolation

In the field of parallel imaging (PI), alongside image-domain regularization methods, substantial research has been dedicated to exploring $k$-space interpolation. However, the interpretability of these methods remains an unresolved issue. Furthermore, these approaches currently face acceleration limitations that are comparable to those experienced by image-domain methods. In order to enhance interpretability and overcome the acceleration limitations, this paper introduces an interpretable framework that unifies both $k$-space interpolation techniques and image-domain methods, grounded in the physical principles of heat diffusion equations. Building upon this foundational framework, a novel $k$-space interpolation method is proposed. Specifically, we model the process of high-frequency information attenuation in $k$-space as a heat diffusion equation, while the effort to reconstruct high-frequency information from low-frequency regions can be conceptualized as a reverse heat equation. However, solving the reverse heat equation poses a challenging inverse problem. To tackle this challenge, we modify the heat equation to align with the principles of magnetic resonance PI physics and employ the score-based generative method to precisely execute the modified reverse heat diffusion. Finally, experimental validation conducted on publicly available datasets demonstrates the superiority of the proposed approach over traditional $k$-space interpolation methods, deep learning-based $k$-space interpolation methods, and conventional diffusion models in terms of reconstruction accuracy, particularly in high-frequency regions.

Meta-Learning Enabled Score-Based Generative Model for 1.5T-Like Image Reconstruction from 0.5T MRI

Magnetic resonance imaging (MRI) is known to have reduced signal-to-noise ratios (SNR) at lower field strengths, leading to signal degradation when producing a low-field MRI image from a high-field one. Therefore, reconstructing a high-field-like image from a low-field MRI is a complex problem due to the ill-posed nature of the task. Additionally, obtaining paired low-field and high-field MR images is often not practical. We theoretically uncovered that the combination of these challenges renders conventional deep learning methods that directly learn the mapping from a low-field MR image to a high-field MR image unsuitable. To overcome these challenges, we introduce a novel meta-learning approach that employs a teacher-student mechanism. Firstly, an optimal-transport-driven teacher learns the degradation process from high-field to low-field MR images and generates pseudo-paired high-field and low-field MRI images. Then, a score-based student solves the inverse problem of reconstructing a high-field-like MR image from a low-field MRI within the framework of iterative regularization, by learning the joint distribution of pseudo-paired images to act as a regularizer. Experimental results on real low-field MRI data demonstrate that our proposed method outperforms state-of-the-art unpaired learning methods.

Deep unfolding as iterative regularization for imaging inverse problems

Recently, deep unfolding methods that guide the design of deep neural networks (DNNs) through iterative algorithms have received increasing attention in the field of inverse problems. Unlike general end-to-end DNNs, unfolding methods have better interpretability and performance. However, to our knowledge, their accuracy and stability in solving inverse problems cannot be fully guaranteed. To bridge this gap, we modified the training procedure and proved that the unfolding method is an iterative regularization method. More precisely, we jointly learn a convex penalty function adversarially by an input-convex neural network (ICNN) to characterize the distance to a real data manifold and train a DNN unfolded from the proximal gradient descent algorithm with this learned penalty. Suppose the real data manifold intersects the inverse problem solutions with only the unique real solution. We prove that the unfolded DNN will converge to it stably. Furthermore, we demonstrate with an example of MRI reconstruction that the proposed method outperforms conventional unfolding methods and traditional regularization methods in terms of reconstruction quality, stability and convergence speed.

Self-Score: Self-Supervised Learning on Score-Based Models for MRI Reconstruction

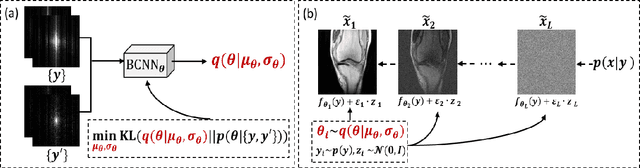
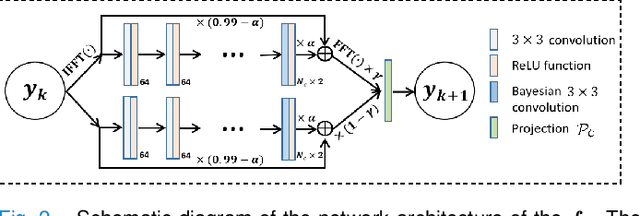
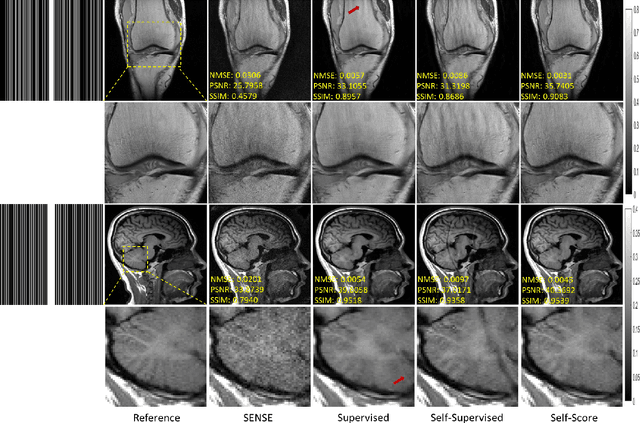
Recently, score-based diffusion models have shown satisfactory performance in MRI reconstruction. Most of these methods require a large amount of fully sampled MRI data as a training set, which, sometimes, is difficult to acquire in practice. This paper proposes a fully-sampled-data-free score-based diffusion model for MRI reconstruction, which learns the fully sampled MR image prior in a self-supervised manner on undersampled data. Specifically, we first infer the fully sampled MR image distribution from the undersampled data by Bayesian deep learning, then perturb the data distribution and approximate their probability density gradient by training a score function. Leveraging the learned score function as a prior, we can reconstruct the MR image by performing conditioned Langevin Markov chain Monte Carlo (MCMC) sampling. Experiments on the public dataset show that the proposed method outperforms existing self-supervised MRI reconstruction methods and achieves comparable performances with the conventional (fully sampled data trained) score-based diffusion methods.

K-UNN: k-Space Interpolation With Untrained Neural Network

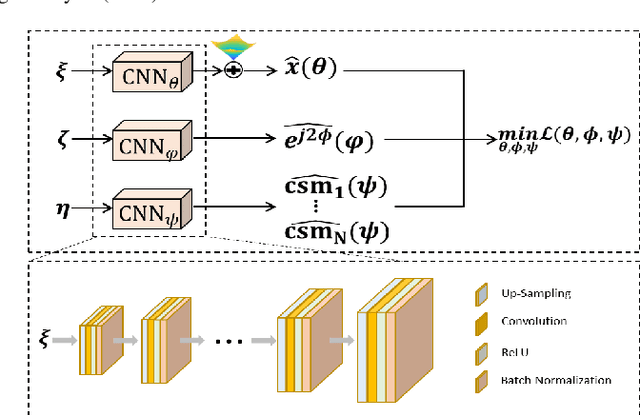
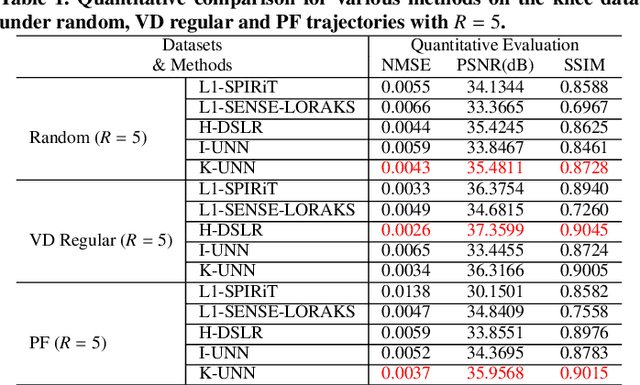
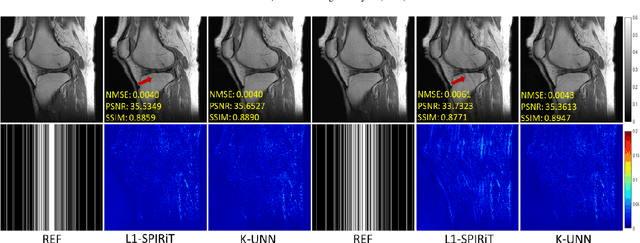
Recently, untrained neural networks (UNNs) have shown satisfactory performances for MR image reconstruction on random sampling trajectories without using additional full-sampled training data. However, the existing UNN-based approach does not fully use the MR image physical priors, resulting in poor performance in some common scenarios (e.g., partial Fourier, regular sampling, etc.) and the lack of theoretical guarantees for reconstruction accuracy. To bridge this gap, we propose a safeguarded k-space interpolation method for MRI using a specially designed UNN with a tripled architecture driven by three physical priors of the MR images (or k-space data), including sparsity, coil sensitivity smoothness, and phase smoothness. We also prove that the proposed method guarantees tight bounds for interpolated k-space data accuracy. Finally, ablation experiments show that the proposed method can more accurately characterize the physical priors of MR images than existing traditional methods. Additionally, under a series of commonly used sampling trajectories, experiments also show that the proposed method consistently outperforms traditional parallel imaging methods and existing UNNs, and even outperforms the state-of-the-art supervised-trained k-space deep learning methods in some cases.

Accelerating Magnetic Resonance Parametric Mapping Using Simultaneously Spatial Patch-based and Parametric Group-based Low-rank Tensors (SMART)

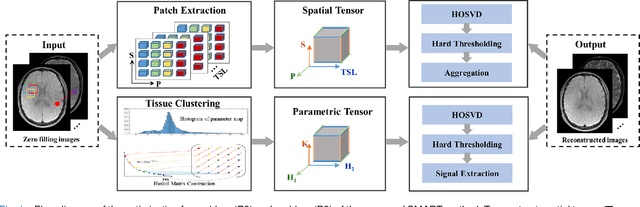
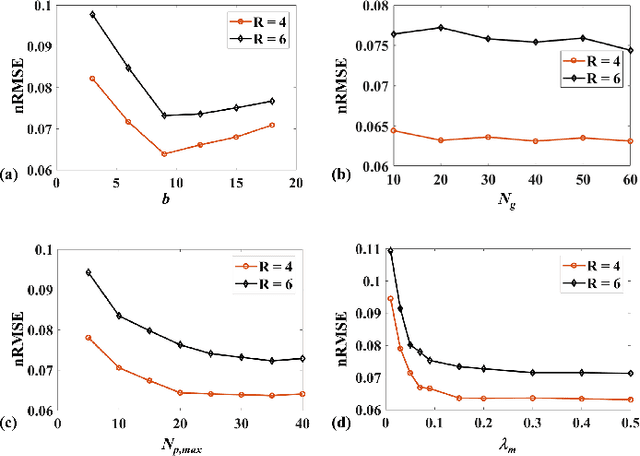
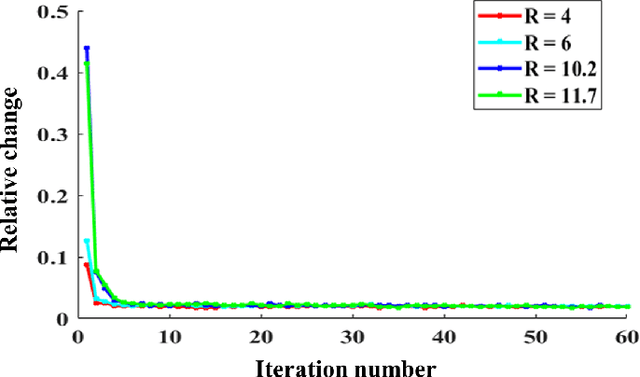
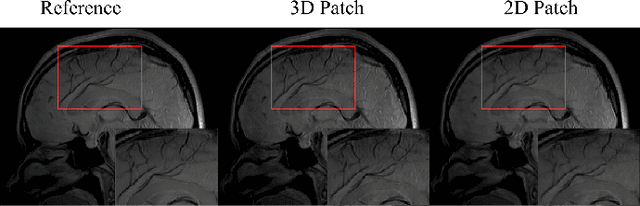
Quantitative magnetic resonance (MR) parametric mapping is a promising approach for characterizing intrinsic tissue-dependent information. However, long scan time significantly hinders its widespread applications. Recently, low-rank tensor has been employed and demonstrated good performance in accelerating MR parametricmapping. In this study, we propose a novel method that uses spatial patch-based and parametric group-based low rank tensors simultaneously (SMART) to reconstruct images from highly undersampled k-space data. The spatial patch-based low-rank tensor exploits the high local and nonlocal redundancies and similarities between the contrast images in parametric mapping. The parametric group based low-rank tensor, which integrates similar exponential behavior of the image signals, is jointly used to enforce the multidimensional low-rankness in the reconstruction process. In vivo brain datasets were used to demonstrate the validity of the proposed method. Experimental results have demonstrated that the proposed method achieves 11.7-fold and 13.21-fold accelerations in two-dimensional and three-dimensional acquisitions, respectively, with more accurate reconstructed images and maps than several state-of-the-art methods. Prospective reconstruction results further demonstrate the capability of the SMART method in accelerating MR quantitative imaging.

PS-Net: Deep Partially Separable Modelling for Dynamic Magnetic Resonance Imaging

Deep learning methods driven by the low-rank regularization have achieved attractive performance in dynamic magnetic resonance (MR) imaging. However, most of these methods represent low-rank prior by hand-crafted nuclear norm, which cannot accurately approximate the low-rank prior over the entire dataset through a fixed regularization parameter. In this paper, we propose a learned low-rank method for dynamic MR imaging. In particular, we unrolled the semi-quadratic splitting method (HQS) algorithm for the partially separable (PS) model to a network, in which the low-rank is adaptively characterized by a learnable null-space transform. Experiments on the cardiac cine dataset show that the proposed model outperforms the state-of-the-art compressed sensing (CS) methods and existing deep learning methods both quantitatively and qualitatively.

Equilibrated Zeroth-Order Unrolled Deep Networks for Accelerated MRI

Recently, model-driven deep learning unrolls a certain iterative algorithm of a regularization model into a cascade network by replacing the first-order information (i.e., (sub)gradient or proximal operator) of the regularizer with a network module, which appears more explainable and predictable compared to common data-driven networks. Conversely, in theory, there is not necessarily such a functional regularizer whose first-order information matches the replaced network module, which means the network output may not be covered by the original regularization model. Moreover, up to now, there is also no theory to guarantee the global convergence and robustness (regularity) of unrolled networks under realistic assumptions. To bridge this gap, this paper propose to present a safeguarded methodology on network unrolling. Specifically, focusing on accelerated MRI, we unroll a zeroth-order algorithm, of which the network module represents the regularizer itself, so that the network output can be still covered by the regularization model. Furthermore, inspired by the ideal of deep equilibrium models, before backpropagating, we carry out the unrolled iterative network to converge to a fixed point to ensure the convergence. In case the measurement data contains noise, we prove that the proposed network is robust against noisy interference. Finally, numerical experiments show that the proposed network consistently outperforms the state-of-the-art MRI reconstruction methods including traditional regularization methods and other deep learning methods.