A Progressive Image Restoration Network for High-order Degradation Imaging in Remote Sensing

Recently, deep learning methods have gained remarkable achievements in the field of image restoration for remote sensing (RS). However, most existing RS image restoration methods focus mainly on conventional first-order degradation models, which may not effectively capture the imaging mechanisms of remote sensing images. Furthermore, many RS image restoration approaches that use deep learning are often criticized for their lacks of architecture transparency and model interpretability. To address these problems, we propose a novel progressive restoration network for high-order degradation imaging (HDI-PRNet), to progressively restore different image degradation. HDI-PRNet is developed based on the theoretical framework of degradation imaging, offering the benefit of mathematical interpretability within the unfolding network. The framework is composed of three main components: a module for image denoising that relies on proximal mapping prior learning, a module for image deblurring that integrates Neumann series expansion with dual-domain degradation learning, and a module for super-resolution. Extensive experiments demonstrate that our method achieves superior performance on both synthetic and real remote sensing images.

MVMS-RCN: A Dual-Domain Unfolding CT Reconstruction with Multi-sparse-view and Multi-scale Refinement-correction

X-ray Computed Tomography (CT) is one of the most important diagnostic imaging techniques in clinical applications. Sparse-view CT imaging reduces the number of projection views to a lower radiation dose and alleviates the potential risk of radiation exposure. Most existing deep learning (DL) and deep unfolding sparse-view CT reconstruction methods: 1) do not fully use the projection data; 2) do not always link their architecture designs to a mathematical theory; 3) do not flexibly deal with multi-sparse-view reconstruction assignments. This paper aims to use mathematical ideas and design optimal DL imaging algorithms for sparse-view tomography reconstructions. We propose a novel dual-domain deep unfolding unified framework that offers a great deal of flexibility for multi-sparse-view CT reconstruction with different sampling views through a single model. This framework combines the theoretical advantages of model-based methods with the superior reconstruction performance of DL-based methods, resulting in the expected generalizability of DL. We propose a refinement module that utilizes unfolding projection domain to refine full-sparse-view projection errors, as well as an image domain correction module that distills multi-scale geometric error corrections to reconstruct sparse-view CT. This provides us with a new way to explore the potential of projection information and a new perspective on designing network architectures. All parameters of our proposed framework are learnable end to end, and our method possesses the potential to be applied to plug-and-play reconstruction. Extensive experiments demonstrate that our framework is superior to other existing state-of-the-art methods. Our source codes are available at https://github.com/fanxiaohong/MVMS-RCN.

A Multi-scale Generalized Shrinkage Threshold Network for Image Blind Deblurring in Remote Sensing

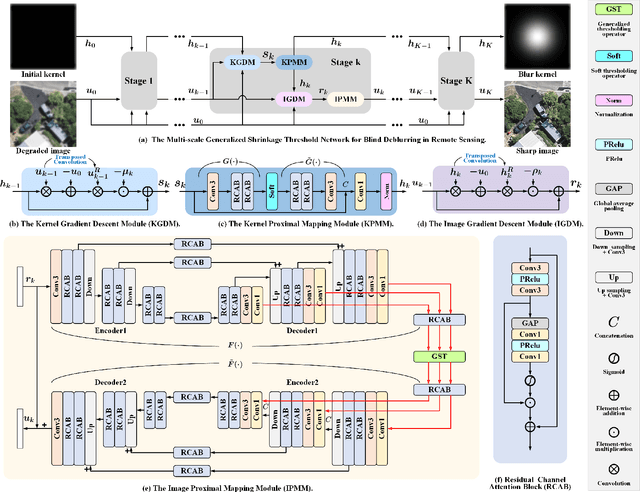
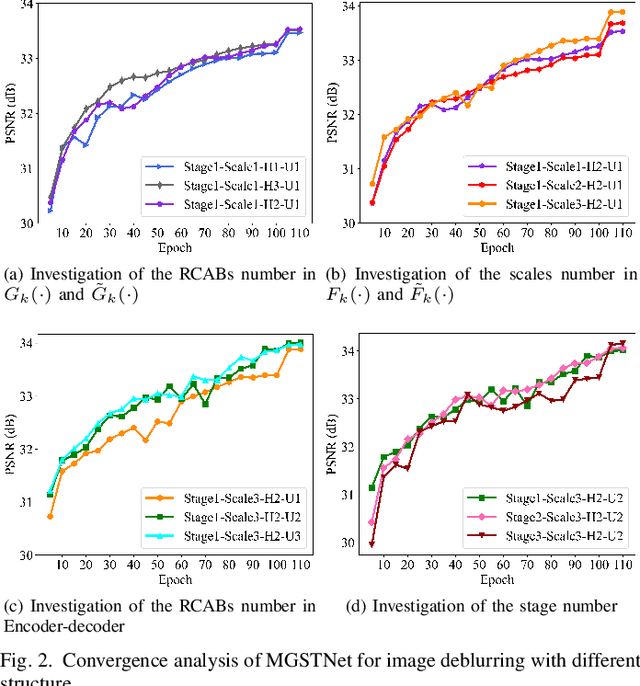
Remote sensing images are essential for many earth science applications, but their quality can be degraded due to limitations in sensor technology and complex imaging environments. To address this, various remote sensing image deblurring methods have been developed to restore sharp, high-quality images from degraded observational data. However, most traditional model-based deblurring methods usually require predefined hand-craft prior assumptions, which are difficult to handle in complex applications, and most deep learning-based deblurring methods are designed as a black box, lacking transparency and interpretability. In this work, we propose a novel blind deblurring learning framework based on alternating iterations of shrinkage thresholds, alternately updating blurring kernels and images, with the theoretical foundation of network design. Additionally, we propose a learnable blur kernel proximal mapping module to improve the blur kernel evaluation in the kernel domain. Then, we proposed a deep proximal mapping module in the image domain, which combines a generalized shrinkage threshold operator and a multi-scale prior feature extraction block. This module also introduces an attention mechanism to adaptively adjust the prior importance, thus avoiding the drawbacks of hand-crafted image prior terms. Thus, a novel multi-scale generalized shrinkage threshold network (MGSTNet) is designed to specifically focus on learning deep geometric prior features to enhance image restoration. Experiments demonstrate the superiority of our MGSTNet framework on remote sensing image datasets compared to existing deblurring methods.

PRISTA-Net: Deep Iterative Shrinkage Thresholding Network for Coded Diffraction Patterns Phase Retrieval

The problem of phase retrieval (PR) involves recovering an unknown image from limited amplitude measurement data and is a challenge nonlinear inverse problem in computational imaging and image processing. However, many of the PR methods are based on black-box network models that lack interpretability and plug-and-play (PnP) frameworks that are computationally complex and require careful parameter tuning. To address this, we have developed PRISTA-Net, a deep unfolding network (DUN) based on the first-order iterative shrinkage thresholding algorithm (ISTA). This network utilizes a learnable nonlinear transformation to address the proximal-point mapping sub-problem associated with the sparse priors, and an attention mechanism to focus on phase information containing image edges, textures, and structures. Additionally, the fast Fourier transform (FFT) is used to learn global features to enhance local information, and the designed logarithmic-based loss function leads to significant improvements when the noise level is low. All parameters in the proposed PRISTA-Net framework, including the nonlinear transformation, threshold parameters, and step size, are learned end-to-end instead of being manually set. This method combines the interpretability of traditional methods with the fast inference ability of deep learning and is able to handle noise at each iteration during the unfolding stage, thus improving recovery quality. Experiments on Coded Diffraction Patterns (CDPs) measurements demonstrate that our approach outperforms the existing state-of-the-art methods in terms of qualitative and quantitative evaluations. Our source codes are available at \emph{https://github.com/liuaxou/PRISTA-Net}.

Physics-Informed DeepMRI: Bridging the Gap from Heat Diffusion to k-Space Interpolation

In the field of parallel imaging (PI), alongside image-domain regularization methods, substantial research has been dedicated to exploring $k$-space interpolation. However, the interpretability of these methods remains an unresolved issue. Furthermore, these approaches currently face acceleration limitations that are comparable to those experienced by image-domain methods. In order to enhance interpretability and overcome the acceleration limitations, this paper introduces an interpretable framework that unifies both $k$-space interpolation techniques and image-domain methods, grounded in the physical principles of heat diffusion equations. Building upon this foundational framework, a novel $k$-space interpolation method is proposed. Specifically, we model the process of high-frequency information attenuation in $k$-space as a heat diffusion equation, while the effort to reconstruct high-frequency information from low-frequency regions can be conceptualized as a reverse heat equation. However, solving the reverse heat equation poses a challenging inverse problem. To tackle this challenge, we modify the heat equation to align with the principles of magnetic resonance PI physics and employ the score-based generative method to precisely execute the modified reverse heat diffusion. Finally, experimental validation conducted on publicly available datasets demonstrates the superiority of the proposed approach over traditional $k$-space interpolation methods, deep learning-based $k$-space interpolation methods, and conventional diffusion models in terms of reconstruction accuracy, particularly in high-frequency regions.

Nest-DGIL: Nesterov-optimized Deep Geometric Incremental Learning for CS Image Reconstruction

Proximal gradient-based optimization is one of the most common strategies for solving image inverse problems as well as easy to implement. However, these techniques often generate heavy artifacts in image reconstruction. One of the most popular refinement methods is to fine-tune the regularization parameter to alleviate such artifacts, but it may not always be sufficient or applicable due to increased computational costs. In this work, we propose a deep geometric incremental learning framework based on second Nesterov proximal gradient optimization. The proposed end-to-end network not only has the powerful learning ability for high/low frequency image features,but also can theoretically guarantee that geometric texture details will be reconstructed from preliminary linear reconstruction.Furthermore, it can avoid the risk of intermediate reconstruction results falling outside the geometric decomposition domains and achieve fast convergence. Our reconstruction framework is decomposed into four modules including general linear reconstruction, cascade geometric incremental restoration, Nesterov acceleration and post-processing. In the image restoration step,a cascade geometric incremental learning module is designed to compensate for the missing texture information from different geometric spectral decomposition domains. Inspired by overlap-tile strategy, we also develop a post-processing module to remove the block-effect in patch-wise-based natural image reconstruction. All parameters in the proposed model are learnable,an adaptive initialization technique of physical-parameters is also employed to make model flexibility and ensure converging smoothly. We compare the reconstruction performance of the proposed method with existing state-of-the-art methods to demonstrate its superiority. Our source codes are available at https://github.com/fanxiaohong/Nest-DGIL.

A Unifying Multi-sampling-ratio CS-MRI Framework With Two-grid-cycle Correction and Geometric Prior Distillation

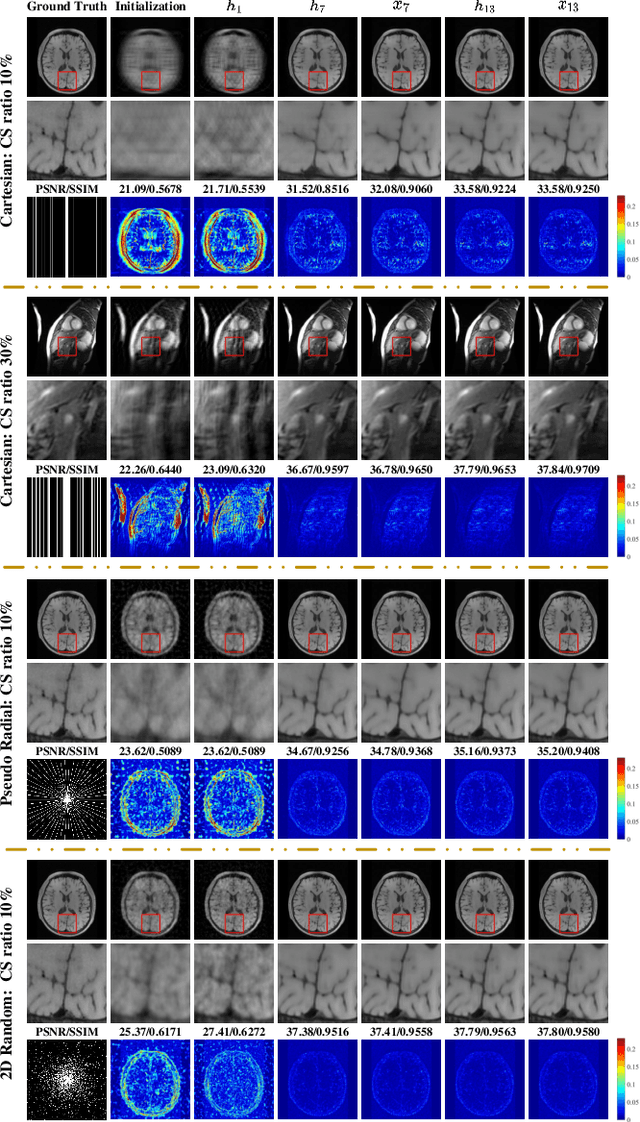
CS is an efficient method to accelerate the acquisition of MR images from under-sampled k-space data. Although existing deep learning CS-MRI methods have achieved considerably impressive performance, explainability and generalizability continue to be challenging for such methods since most of them are not flexible enough to handle multi-sampling-ratio reconstruction assignments, often the transition from mathematical analysis to network design not always natural enough. In this work, to tackle explainability and generalizability, we propose a unifying deep unfolding multi-sampling-ratio CS-MRI framework, by merging advantages of model-based and deep learning-based methods. The combined approach offers more generalizability than previous works whereas deep learning gains explainability through a geometric prior module. Inspired by multigrid algorithm, we first embed the CS-MRI-based optimization algorithm into correction-distillation scheme that consists of three ingredients: pre-relaxation module, correction module and geometric prior distillation module. Furthermore, we employ a condition module to learn adaptively step-length and noise level from compressive sampling ratio in every stage, which enables the proposed framework to jointly train multi-ratio tasks through a single model. The proposed model can not only compensate the lost contextual information of reconstructed image which is refined from low frequency error in geometric characteristic k-space, but also integrate the theoretical guarantee of model-based methods and the superior reconstruction performances of deep learning-based methods. All physical-model parameters are learnable, and numerical experiments show that our framework outperforms state-of-the-art methods in terms of qualitative and quantitative evaluations.

Deep Geometric Distillation Network for Compressive Sensing MRI

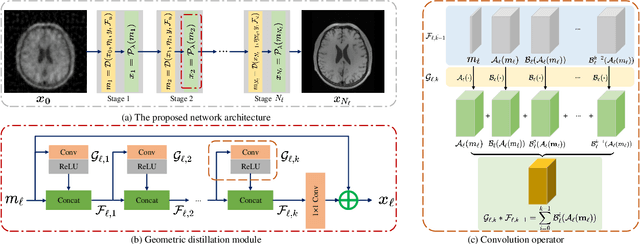
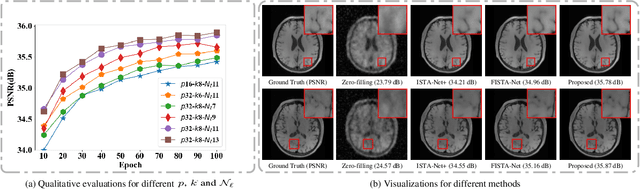
Compressed sensing (CS) is an efficient method to reconstruct MR image from small sampled data in $k$-space and accelerate the acquisition of MRI. In this work, we propose a novel deep geometric distillation network which combines the merits of model-based and deep learning-based CS-MRI methods, it can be theoretically guaranteed to improve geometric texture details of a linear reconstruction. Firstly, we unfold the model-based CS-MRI optimization problem into two sub-problems that consist of image linear approximation and image geometric compensation. Secondly, geometric compensation sub-problem for distilling lost texture details in approximation stage can be expanded by Taylor expansion to design a geometric distillation module fusing features of different geometric characteristic domains. Additionally, we use a learnable version with adaptive initialization of the step-length parameter, which allows model more flexibility that can lead to convergent smoothly. Numerical experiments verify its superiority over other state-of-the-art CS-MRI reconstruction approaches. The source code will be available at \url{https://github.com/fanxiaohong/Deep-Geometric-Distillation-Network-for-CS-MRI}