Zhilang Qiu
K-UNN: k-Space Interpolation With Untrained Neural Network
Aug 11, 2022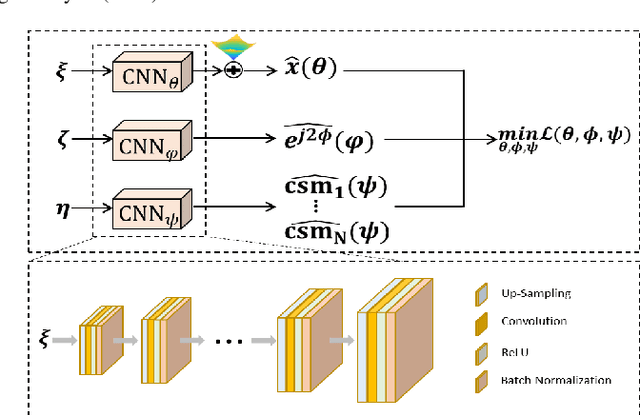
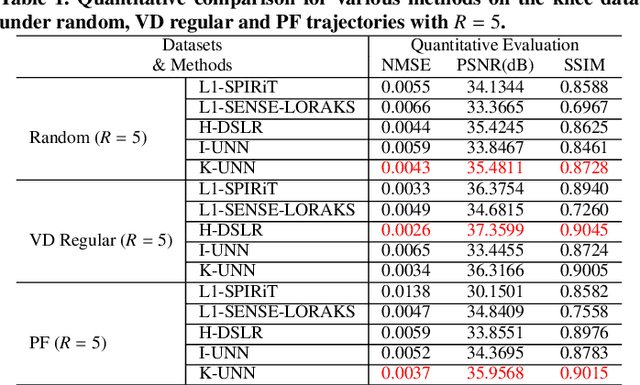

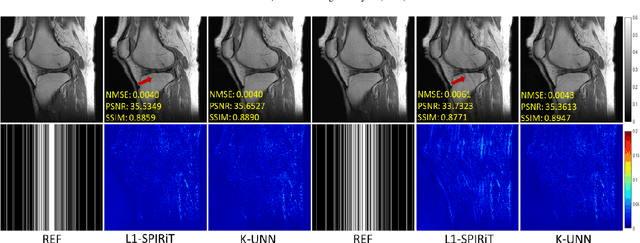
Abstract:Recently, untrained neural networks (UNNs) have shown satisfactory performances for MR image reconstruction on random sampling trajectories without using additional full-sampled training data. However, the existing UNN-based approach does not fully use the MR image physical priors, resulting in poor performance in some common scenarios (e.g., partial Fourier, regular sampling, etc.) and the lack of theoretical guarantees for reconstruction accuracy. To bridge this gap, we propose a safeguarded k-space interpolation method for MRI using a specially designed UNN with a tripled architecture driven by three physical priors of the MR images (or k-space data), including sparsity, coil sensitivity smoothness, and phase smoothness. We also prove that the proposed method guarantees tight bounds for interpolated k-space data accuracy. Finally, ablation experiments show that the proposed method can more accurately characterize the physical priors of MR images than existing traditional methods. Additionally, under a series of commonly used sampling trajectories, experiments also show that the proposed method consistently outperforms traditional parallel imaging methods and existing UNNs, and even outperforms the state-of-the-art supervised-trained k-space deep learning methods in some cases.
Deep Low-rank plus Sparse Network for Dynamic MR Imaging
Oct 26, 2020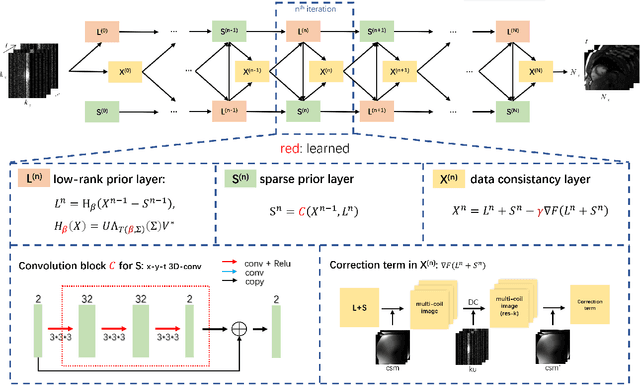
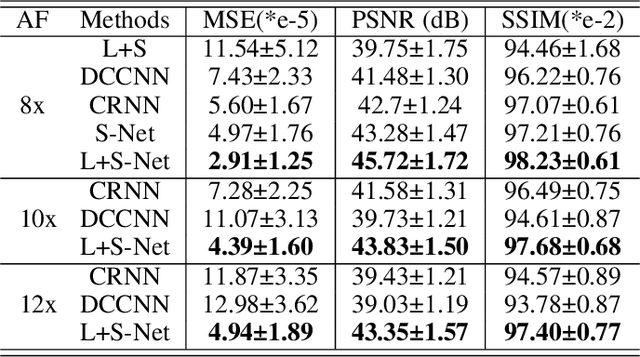


Abstract:In dynamic MR imaging, L+S decomposition, or robust PCA equivalently, has achieved stunning performance. However, the selection of parameters of L+S is empirical, and the acceleration rate is limited, which are the common failings of iterative CS-MRI reconstruction methods. Many deep learning approaches were proposed to address these issues, but few of them used the low-rank prior. In this paper, a model-based low-rank plus sparse network, dubbed as L+S-Net, is proposed for dynamic MR reconstruction. In particular, we use an alternating linearized minimization method to solve the optimization problem with low-rank and sparse regularization. A learned soft singular value thresholding is introduced to make sure the clear separation of L component and S component. Then the iterative steps is unrolled into a network whose regularization parameters are learnable. Experiments on retrospective and prospective cardiac cine dataset show that the proposed model outperforms the state-of-the-art CS and existing deep learning methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge