SwitchHead: Accelerating Transformers with Mixture-of-Experts Attention

The costly self-attention layers in modern Transformers require memory and compute quadratic in sequence length. Existing approximation methods usually underperform and fail to obtain significant speedups in practice. Here we present SwitchHead - a novel method that reduces both compute and memory requirements and achieves wall-clock speedup, while matching the language modeling performance of baseline Transformers with the same parameter budget. SwitchHead uses Mixture-of-Experts (MoE) layers for the value and output projections and requires 4 to 8 times fewer attention matrices than standard Transformers. Our novel attention can also be combined with MoE MLP layers, resulting in an efficient fully-MoE "SwitchAll" Transformer model. Our code is public.

Mindstorms in Natural Language-Based Societies of Mind

Both Minsky's "society of mind" and Schmidhuber's "learning to think" inspire diverse societies of large multimodal neural networks (NNs) that solve problems by interviewing each other in a "mindstorm." Recent implementations of NN-based societies of minds consist of large language models (LLMs) and other NN-based experts communicating through a natural language interface. In doing so, they overcome the limitations of single LLMs, improving multimodal zero-shot reasoning. In these natural language-based societies of mind (NLSOMs), new agents -- all communicating through the same universal symbolic language -- are easily added in a modular fashion. To demonstrate the power of NLSOMs, we assemble and experiment with several of them (having up to 129 members), leveraging mindstorms in them to solve some practical AI tasks: visual question answering, image captioning, text-to-image synthesis, 3D generation, egocentric retrieval, embodied AI, and general language-based task solving. We view this as a starting point towards much larger NLSOMs with billions of agents-some of which may be humans. And with this emergence of great societies of heterogeneous minds, many new research questions have suddenly become paramount to the future of artificial intelligence. What should be the social structure of an NLSOM? What would be the (dis)advantages of having a monarchical rather than a democratic structure? How can principles of NN economies be used to maximize the total reward of a reinforcement learning NLSOM? In this work, we identify, discuss, and try to answer some of these questions.

Fast and Precise: Adjusting Planning Horizon with Adaptive Subgoal Search

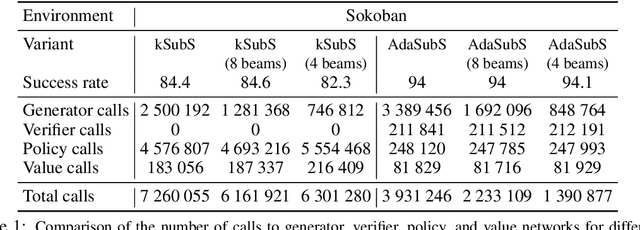
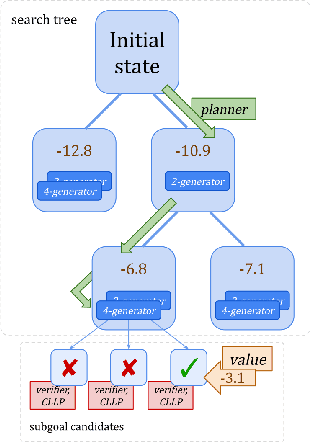
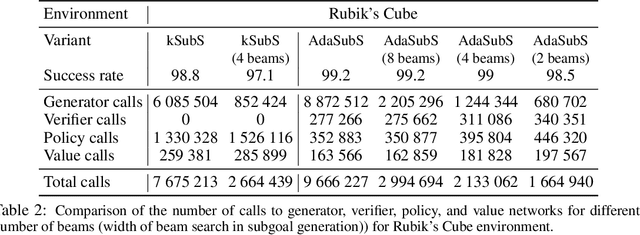
Complex reasoning problems contain states that vary in the computational cost required to determine a good action plan. Taking advantage of this property, we propose Adaptive Subgoal Search (AdaSubS), a search method that adaptively adjusts the planning horizon. To this end, AdaSubS generates diverse sets of subgoals at different distances. A verification mechanism is employed to filter out unreachable subgoals swiftly and thus allowing to focus on feasible further subgoals. In this way, AdaSubS benefits from the efficiency of planning with longer subgoals and the fine control with the shorter ones. We show that AdaSubS significantly surpasses hierarchical planning algorithms on three complex reasoning tasks: Sokoban, the Rubik's Cube, and inequality proving benchmark INT, setting new state-of-the-art on INT.

Measuring and Improving BERT's Mathematical Abilities by Predicting the Order of Reasoning

Imagine you are in a supermarket. You have two bananas in your basket and want to buy four apples. How many fruits do you have in total? This seemingly straightforward question can be challenging for data-driven language models, even if trained at scale. However, we would expect such generic language models to possess some mathematical abilities in addition to typical linguistic competence. Towards this goal, we investigate if a commonly used language model, BERT, possesses such mathematical abilities and, if so, to what degree. For that, we fine-tune BERT on a popular dataset for word math problems, AQuA-RAT, and conduct several tests to understand learned representations better. Since we teach models trained on natural language to do formal mathematics, we hypothesize that such models would benefit from training on semi-formal steps that explain how math results are derived. To better accommodate such training, we also propose new pretext tasks for learning mathematical rules. We call them (Neighbor) Reasoning Order Prediction (ROP or NROP). With this new model, we achieve significantly better outcomes than data-driven baselines and even on-par with more tailored models. We also show how to reduce positional bias in such models.