Scaling Laws for Fine-Grained Mixture of Experts

Mixture of Experts (MoE) models have emerged as a primary solution for reducing the computational cost of Large Language Models. In this work, we analyze their scaling properties, incorporating an expanded range of variables. Specifically, we introduce a new hyperparameter, granularity, whose adjustment enables precise control over the size of the experts. Building on this, we establish scaling laws for fine-grained MoE, taking into account the number of training tokens, model size, and granularity. Leveraging these laws, we derive the optimal training configuration for a given computational budget. Our findings not only show that MoE models consistently outperform dense Transformers but also highlight that the efficiency gap between dense and MoE models widens as we scale up the model size and training budget. Furthermore, we demonstrate that the common practice of setting the size of experts in MoE to mirror the feed-forward layer is not optimal at almost any computational budget.

Mixture of Tokens: Efficient LLMs through Cross-Example Aggregation

Despite the promise of Mixture of Experts (MoE) models in increasing parameter counts of Transformer models while maintaining training and inference costs, their application carries notable drawbacks. The key strategy of these models is to, for each processed token, activate at most a few experts - subsets of an extensive feed-forward layer. But this approach is not without its challenges. The operation of matching experts and tokens is discrete, which makes MoE models prone to issues like training instability and uneven expert utilization. Existing techniques designed to address these concerns, such as auxiliary losses or balance-aware matching, result either in lower model performance or are more difficult to train. In response to these issues, we propose Mixture of Tokens, a fully-differentiable model that retains the benefits of MoE architectures while avoiding the aforementioned difficulties. Rather than routing tokens to experts, this approach mixes tokens from different examples prior to feeding them to experts, enabling the model to learn from all token-expert combinations. Importantly, this mixing can be disabled to avoid mixing of different sequences during inference. Crucially, this method is fully compatible with both masked and causal Large Language Model training and inference.

Fast and Precise: Adjusting Planning Horizon with Adaptive Subgoal Search

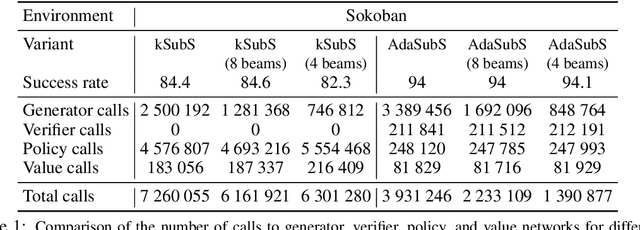
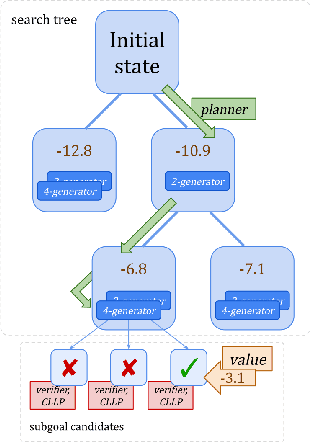
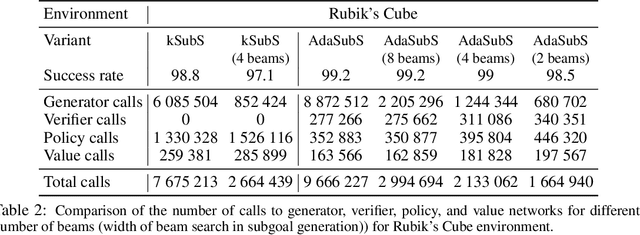
Complex reasoning problems contain states that vary in the computational cost required to determine a good action plan. Taking advantage of this property, we propose Adaptive Subgoal Search (AdaSubS), a search method that adaptively adjusts the planning horizon. To this end, AdaSubS generates diverse sets of subgoals at different distances. A verification mechanism is employed to filter out unreachable subgoals swiftly and thus allowing to focus on feasible further subgoals. In this way, AdaSubS benefits from the efficiency of planning with longer subgoals and the fine control with the shorter ones. We show that AdaSubS significantly surpasses hierarchical planning algorithms on three complex reasoning tasks: Sokoban, the Rubik's Cube, and inequality proving benchmark INT, setting new state-of-the-art on INT.

Thor: Wielding Hammers to Integrate Language Models and Automated Theorem Provers

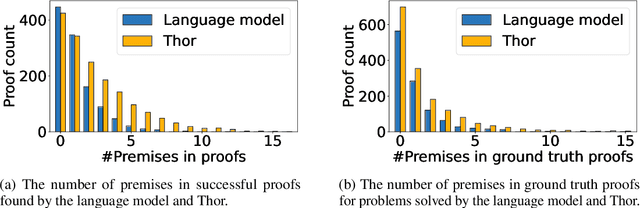
In theorem proving, the task of selecting useful premises from a large library to unlock the proof of a given conjecture is crucially important. This presents a challenge for all theorem provers, especially the ones based on language models, due to their relative inability to reason over huge volumes of premises in text form. This paper introduces Thor, a framework integrating language models and automated theorem provers to overcome this difficulty. In Thor, a class of methods called hammers that leverage the power of automated theorem provers are used for premise selection, while all other tasks are designated to language models. Thor increases a language model's success rate on the PISA dataset from $39\%$ to $57\%$, while solving $8.2\%$ of problems neither language models nor automated theorem provers are able to solve on their own. Furthermore, with a significantly smaller computational budget, Thor can achieve a success rate on the MiniF2F dataset that is on par with the best existing methods. Thor can be instantiated for the majority of popular interactive theorem provers via a straightforward protocol we provide.

Subgoal Search For Complex Reasoning Tasks

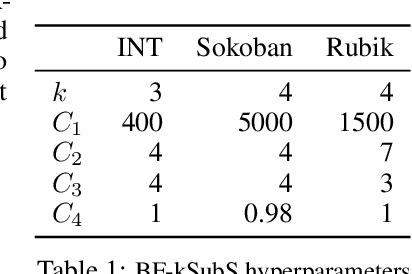
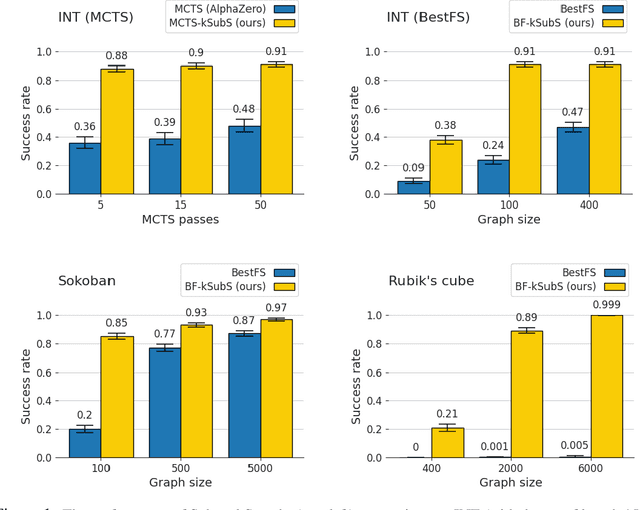
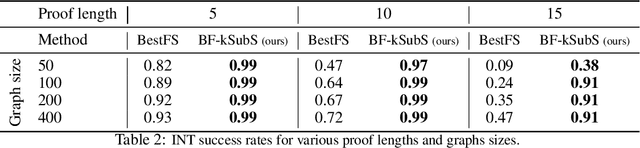
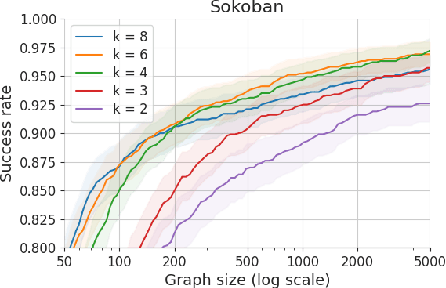
Humans excel in solving complex reasoning tasks through a mental process of moving from one idea to a related one. Inspired by this, we propose Subgoal Search (kSubS) method. Its key component is a learned subgoal generator that produces a diversity of subgoals that are both achievable and closer to the solution. Using subgoals reduces the search space and induces a high-level search graph suitable for efficient planning. In this paper, we implement kSubS using a transformer-based subgoal module coupled with the classical best-first search framework. We show that a simple approach of generating $k$-th step ahead subgoals is surprisingly efficient on three challenging domains: two popular puzzle games, Sokoban and the Rubik's Cube, and an inequality proving benchmark INT. kSubS achieves strong results including state-of-the-art on INT within a modest computational budget.