Publicly Detectable Watermarking for Language Models

We construct the first provable watermarking scheme for language models with public detectability or verifiability: we use a private key for watermarking and a public key for watermark detection. Our protocol is the first watermarking scheme that does not embed a statistical signal in generated text. Rather, we directly embed a publicly-verifiable cryptographic signature using a form of rejection sampling. We show that our construction meets strong formal security guarantees and preserves many desirable properties found in schemes in the private-key watermarking setting. In particular, our watermarking scheme retains distortion-freeness and model agnosticity. We implement our scheme and make empirical measurements over open models in the 7B parameter range. Our experiments suggest that our watermarking scheme meets our formal claims while preserving text quality.

On Optimal Learning Under Targeted Data Poisoning

Consider the task of learning a hypothesis class $\mathcal{H}$ in the presence of an adversary that can replace up to an $\eta$ fraction of the examples in the training set with arbitrary adversarial examples. The adversary aims to fail the learner on a particular target test point $x$ which is known to the adversary but not to the learner. In this work we aim to characterize the smallest achievable error $\epsilon=\epsilon(\eta)$ by the learner in the presence of such an adversary in both realizable and agnostic settings. We fully achieve this in the realizable setting, proving that $\epsilon=\Theta(\mathtt{VC}(\mathcal{H})\cdot \eta)$, where $\mathtt{VC}(\mathcal{H})$ is the VC dimension of $\mathcal{H}$. Remarkably, we show that the upper bound can be attained by a deterministic learner. In the agnostic setting we reveal a more elaborate landscape: we devise a deterministic learner with a multiplicative regret guarantee of $\epsilon \leq C\cdot\mathtt{OPT} + O(\mathtt{VC}(\mathcal{H})\cdot \eta)$, where $C > 1$ is a universal numerical constant. We complement this by showing that for any deterministic learner there is an attack which worsens its error to at least $2\cdot \mathtt{OPT}$. This implies that a multiplicative deterioration in the regret is unavoidable in this case. Finally, the algorithms we develop for achieving the optimal rates are inherently improper. Nevertheless, we show that for a variety of natural concept classes, such as linear classifiers, it is possible to retain the dependence $\epsilon=\Theta_{\mathcal{H}}(\eta)$ by a proper algorithm in the realizable setting. Here $\Theta_{\mathcal{H}}$ conceals a polynomial dependence on $\mathtt{VC}(\mathcal{H})$.

Overparameterized (robust) models from computational constraints

Overparameterized models with millions of parameters have been hugely successful. In this work, we ask: can the need for large models be, at least in part, due to the \emph{computational} limitations of the learner? Additionally, we ask, is this situation exacerbated for \emph{robust} learning? We show that this indeed could be the case. We show learning tasks for which computationally bounded learners need \emph{significantly more} model parameters than what information-theoretic learners need. Furthermore, we show that even more model parameters could be necessary for robust learning. In particular, for computationally bounded learners, we extend the recent result of Bubeck and Sellke [NeurIPS'2021] which shows that robust models might need more parameters, to the computational regime and show that bounded learners could provably need an even larger number of parameters. Then, we address the following related question: can we hope to remedy the situation for robust computationally bounded learning by restricting \emph{adversaries} to also be computationally bounded for sake of obtaining models with fewer parameters? Here again, we show that this could be possible. Specifically, building on the work of Garg, Jha, Mahloujifar, and Mahmoody [ALT'2020], we demonstrate a learning task that can be learned efficiently and robustly against a computationally bounded attacker, while to be robust against an information-theoretic attacker requires the learner to utilize significantly more parameters.

Deletion Inference, Reconstruction, and Compliance in Machine (Un)Learning

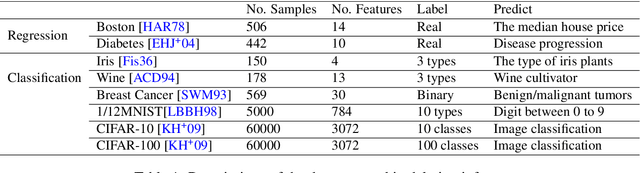
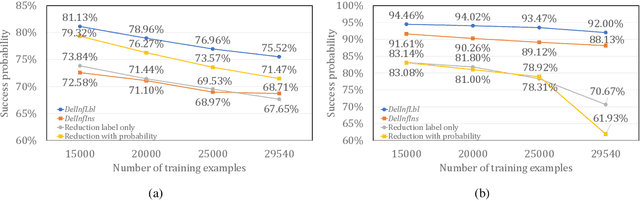
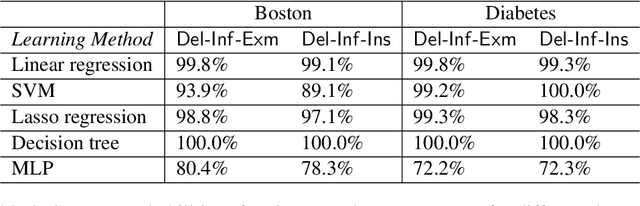
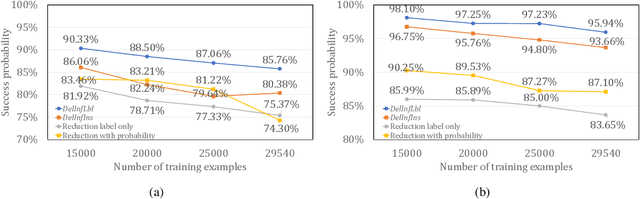
Privacy attacks on machine learning models aim to identify the data that is used to train such models. Such attacks, traditionally, are studied on static models that are trained once and are accessible by the adversary. Motivated to meet new legal requirements, many machine learning methods are recently extended to support machine unlearning, i.e., updating models as if certain examples are removed from their training sets, and meet new legal requirements. However, privacy attacks could potentially become more devastating in this new setting, since an attacker could now access both the original model before deletion and the new model after the deletion. In fact, the very act of deletion might make the deleted record more vulnerable to privacy attacks. Inspired by cryptographic definitions and the differential privacy framework, we formally study privacy implications of machine unlearning. We formalize (various forms of) deletion inference and deletion reconstruction attacks, in which the adversary aims to either identify which record is deleted or to reconstruct (perhaps part of) the deleted records. We then present successful deletion inference and reconstruction attacks for a variety of machine learning models and tasks such as classification, regression, and language models. Finally, we show that our attacks would provably be precluded if the schemes satisfy (variants of) Deletion Compliance (Garg, Goldwasser, and Vasudevan, Eurocrypt' 20).

Learning and Certification under Instance-targeted Poisoning

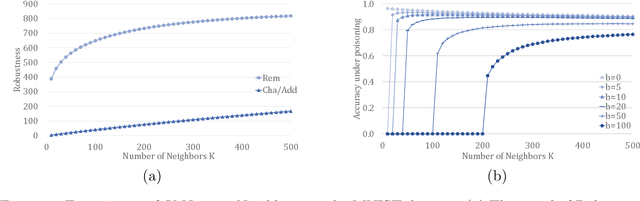
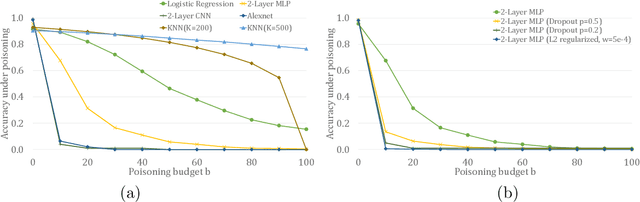
In this paper, we study PAC learnability and certification under instance-targeted poisoning attacks, where the adversary may change a fraction of the training set with the goal of fooling the learner at a specific target instance. Our first contribution is to formalize the problem in various settings, and explicitly discussing subtle aspects such as learner's randomness and whether (or not) adversary's attack can depend on it. We show that when the budget of the adversary scales sublinearly with the sample complexity, PAC learnability and certification are achievable. In contrast, when the adversary's budget grows linearly with the sample complexity, the adversary can potentially drive up the expected 0-1 loss to one. We further extend our results to distribution-specific PAC learning in the same attack model and show that proper learning with certification is possible for learning halfspaces under Gaussian distribution. Finally, we empirically study the robustness of K nearest neighbour, logistic regression, multi-layer perceptron, and convolutional neural network on real data sets, and test them against targeted-poisoning attacks. Our experimental results show that many models, especially state-of-the-art neural networks, are indeed vulnerable to these strong attacks. Interestingly, we observe that methods with high standard accuracy might be more vulnerable to instance-targeted poisoning attacks.

An Attack on InstaHide: Is Private Learning Possible with Instance Encoding?

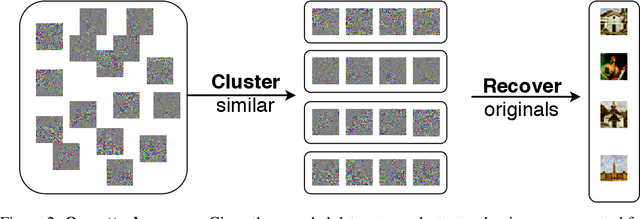
A learning algorithm is private if the produced model does not reveal (too much) about its training set. InstaHide [Huang, Song, Li, Arora, ICML'20] is a recent proposal that claims to preserve privacy by an encoding mechanism that modifies the inputs before being processed by the normal learner. We present a reconstruction attack on InstaHide that is able to use the encoded images to recover visually recognizable versions of the original images. Our attack is effective and efficient, and empirically breaks InstaHide on CIFAR-10, CIFAR-100, and the recently released InstaHide Challenge. We further formalize various privacy notions of learning through instance encoding and investigate the possibility of achieving these notions. We prove barriers against achieving (indistinguishability based notions of) privacy through any learning protocol that uses instance encoding.

Obliviousness Makes Poisoning Adversaries Weaker

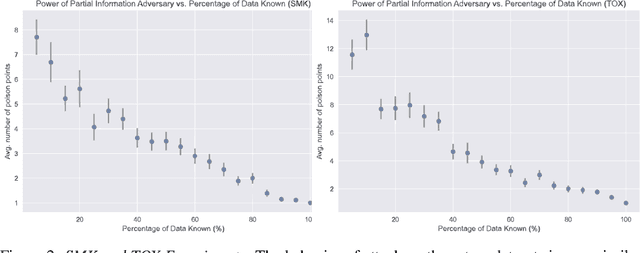
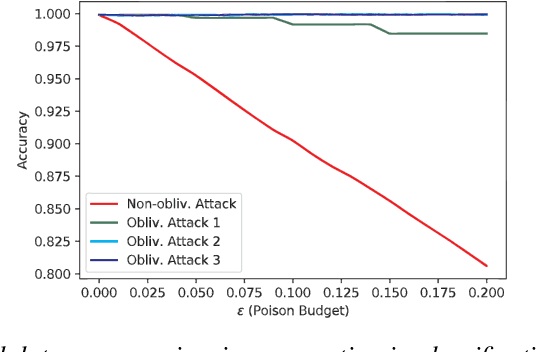
Poisoning attacks have emerged as a significant security threat to machine learning (ML) algorithms. It has been demonstrated that adversaries who make small changes to the training set, such as adding specially crafted data points, can hurt the performance of the output model. Most of these attacks require the full knowledge of training data or the underlying data distribution. In this paper we study the power of oblivious adversaries who do not have any information about the training set. We show a separation between oblivious and full-information poisoning adversaries. Specifically, we construct a sparse linear regression problem for which LASSO estimator is robust against oblivious adversaries whose goal is to add a non-relevant features to the model with certain poisoning budget. On the other hand, non-oblivious adversaries, with the same budget, can craft poisoning examples based on the rest of the training data and successfully add non-relevant features to the model.

Computational Concentration of Measure: Optimal Bounds, Reductions, and More

Product measures of dimension $n$ are known to be concentrated in Hamming distance: for any set $S$ in the product space of probability $\epsilon$, a random point in the space, with probability $1-\delta$, has a neighbor in $S$ that is different from the original point in only $O(\sqrt{n\ln(1/(\epsilon\delta))})$ coordinates. We obtain the tight computational version of this result, showing how given a random point and access to an $S$-membership oracle, we can find such a close point in polynomial time. This resolves an open question of [Mahloujifar and Mahmoody, ALT 2019]. As corollaries, we obtain polynomial-time poisoning and (in certain settings) evasion attacks against learning algorithms when the original vulnerabilities have any cryptographically non-negligible probability. We call our algorithm MUCIO ("MUltiplicative Conditional Influence Optimizer") since proceeding through the coordinates, it decides to change each coordinate of the given point based on a multiplicative version of the influence of that coordinate, where influence is computed conditioned on previously updated coordinates. We also define a new notion of algorithmic reduction between computational concentration of measure in different metric probability spaces. As an application, we get computational concentration of measure for high-dimensional Gaussian distributions under the $\ell_1$ metric. We prove several extensions to the results above: (1) Our computational concentration result is also true when the Hamming distance is weighted. (2) We obtain an algorithmic version of concentration around mean, more specifically, McDiarmid's inequality. (3) Our result generalizes to discrete random processes, and this leads to new tampering algorithms for collective coin tossing protocols. (4) We prove exponential lower bounds on the average running time of non-adaptive query algorithms.

Lower Bounds for Adversarially Robust PAC Learning

In this work, we initiate a formal study of probably approximately correct (PAC) learning under evasion attacks, where the adversary's goal is to \emph{misclassify} the adversarially perturbed sample point $\widetilde{x}$, i.e., $h(\widetilde{x})\neq c(\widetilde{x})$, where $c$ is the ground truth concept and $h$ is the learned hypothesis. Previous work on PAC learning of adversarial examples have all modeled adversarial examples as corrupted inputs in which the goal of the adversary is to achieve $h(\widetilde{x}) \neq c(x)$, where $x$ is the original untampered instance. These two definitions of adversarial risk coincide for many natural distributions, such as images, but are incomparable in general. We first prove that for many theoretically natural input spaces of high dimension $n$ (e.g., isotropic Gaussian in dimension $n$ under $\ell_2$ perturbations), if the adversary is allowed to apply up to a sublinear $o(||x||)$ amount of perturbations on the test instances, PAC learning requires sample complexity that is exponential in $n$. This is in contrast with results proved using the corrupted-input framework, in which the sample complexity of robust learning is only polynomially more. We then formalize hybrid attacks in which the evasion attack is preceded by a poisoning attack. This is perhaps reminiscent of "trapdoor attacks" in which a poisoning phase is involved as well, but the evasion phase here uses the error-region definition of risk that aims at misclassifying the perturbed instances. In this case, we show PAC learning is sometimes impossible all together, even when it is possible without the attack (e.g., due to the bounded VC dimension).

Empirically Measuring Concentration: Fundamental Limits on Intrinsic Robustness

Many recent works have shown that adversarial examples that fool classifiers can be found by minimally perturbing a normal input. Recent theoretical results, starting with Gilmer et al. (2018), show that if the inputs are drawn from a concentrated metric probability space, then adversarial examples with small perturbation are inevitable. A concentrated space has the property that any subset with $\Omega(1)$ (e.g., 1/100) measure, according to the imposed distribution, has small distance to almost all (e.g., 99/100) of the points in the space. It is not clear, however, whether these theoretical results apply to actual distributions such as images. This paper presents a method for empirically measuring and bounding the concentration of a concrete dataset which is proven to converge to the actual concentration. We use it to empirically estimate the intrinsic robustness to $\ell_\infty$ and $\ell_2$ perturbations of several image classification benchmarks.